Figure shows a current loop having two circular arcs joined by two lines. Find the magnitude field B at the centre O.
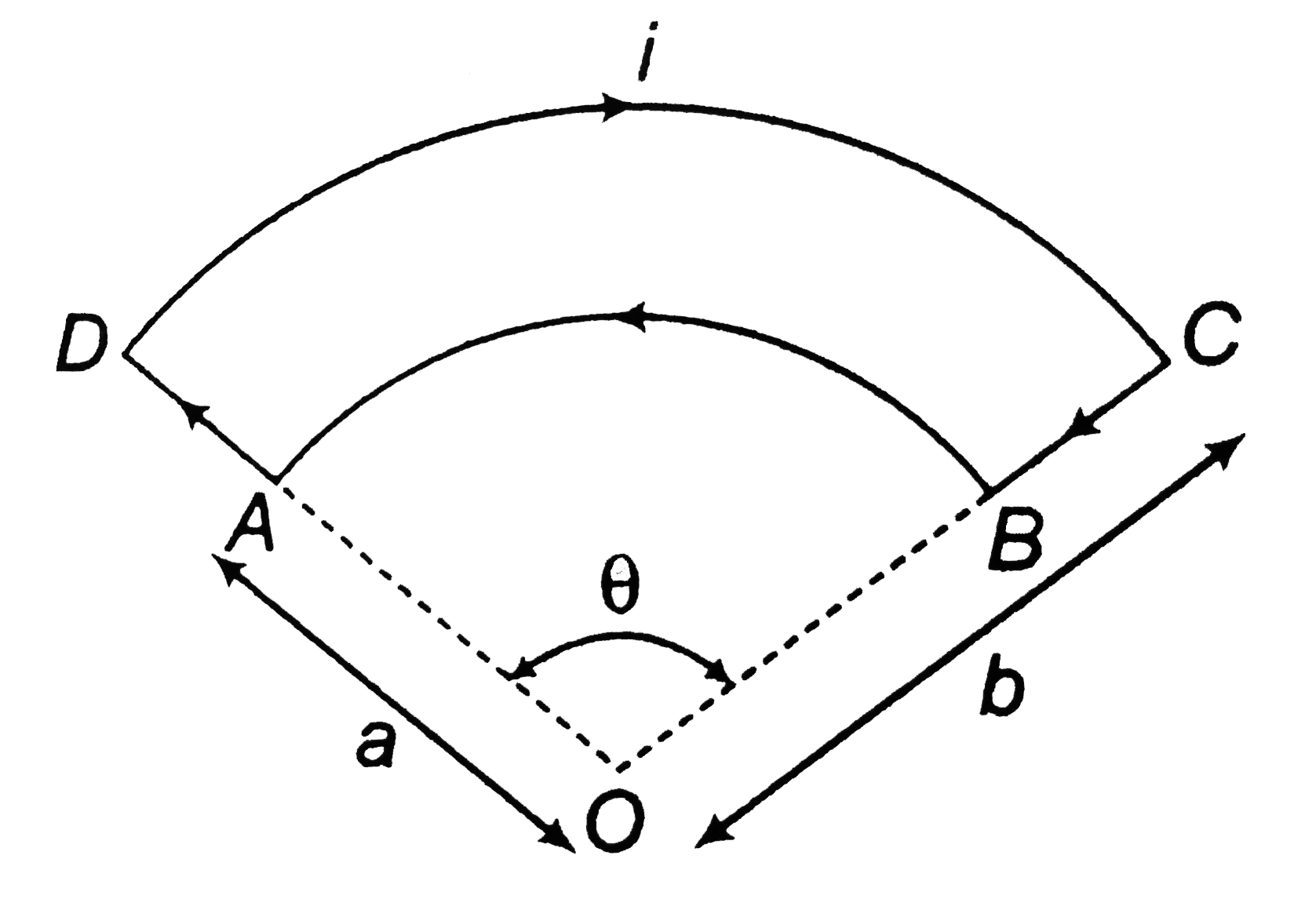
Magnetic field at point O due to wire CB and AD will be zero.
Magnetic field due to wire BA will be
B1=(θ2π)(μ0i2a)
Direction of field B1 is coming out of the plane of the figure.
Similarly, field at O due to DC will be
B2=(θ2π)(μ0i2b)
Direction of field B2 is going into the plane of the figure. The resultant field at O is
B=B1−B2=μ0θ(b−a)4πab
Similar Questions
Figure shows a current loop having two circular arcs joined by two radial lines. Find the magnetic field B at the centre O.

View SolutionA current loop, having two circular arcs jo ined by two radial lines is shown in the figure. It carries a current of 10 A. The magnetic field at point O will be close to :
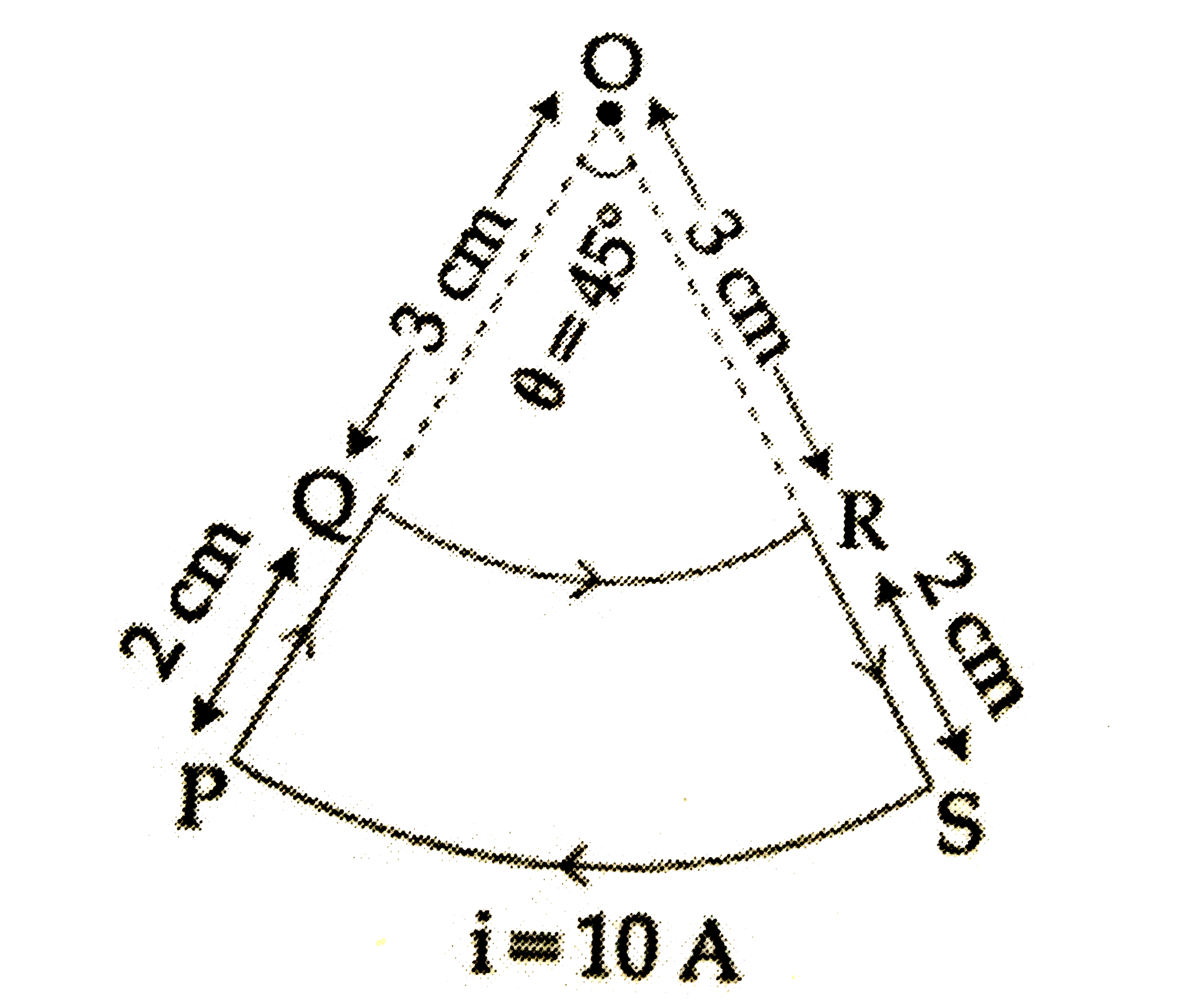
View Solution
Knowledge Check
A cell is connected between two points of a uniformly thick circular conductor and i1andi2 are the currents flowing in two parts of the circular conductor of radius a The magnetic field at the centre of the loop will be
AzeroBμ04π(I1−I2)Cμ02a(I1+I2)Dμ0a(I1+I2)A part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
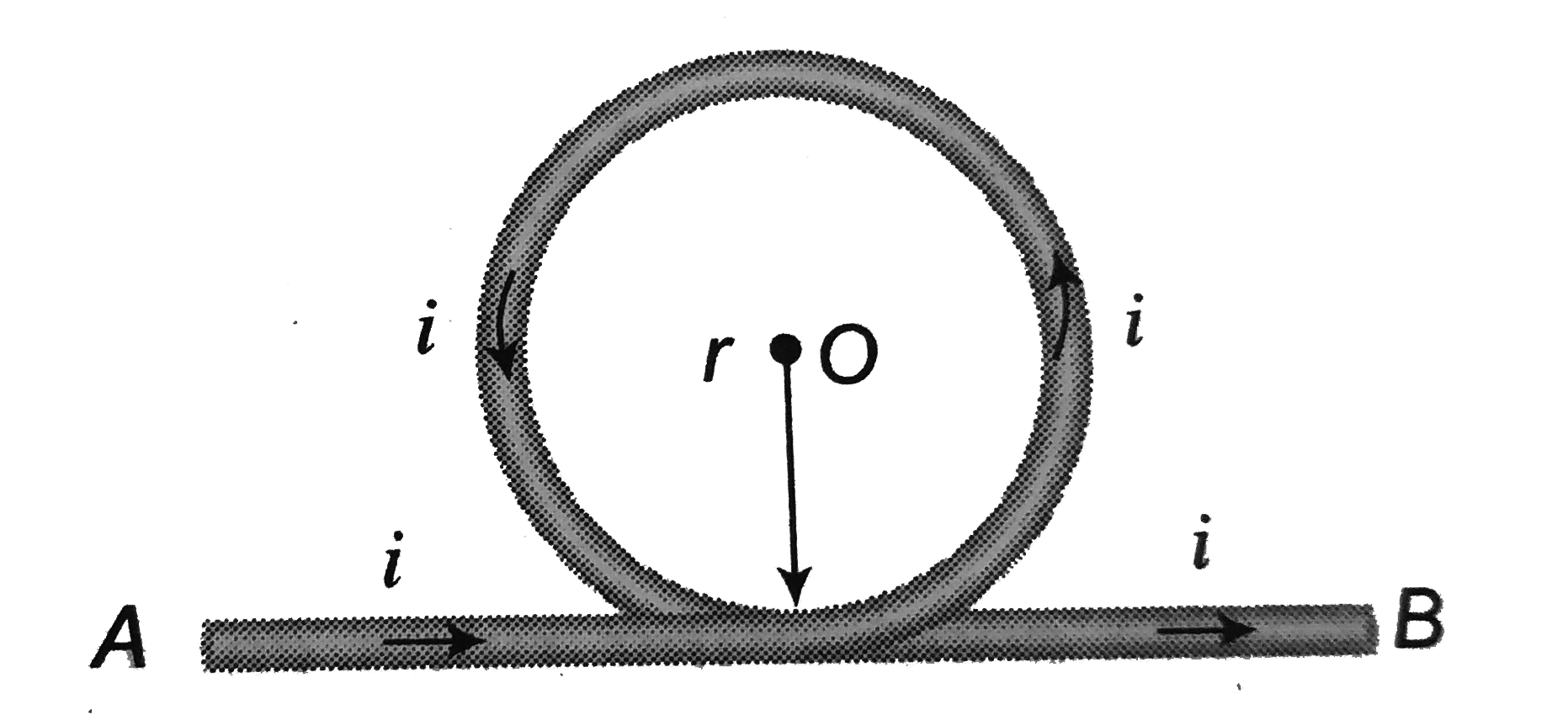 Aμ0i4rBμ0i2rCμ0i2πr(π+1)Dμ0i2πr(π−1)
Aμ0i4rBμ0i2rCμ0i2πr(π+1)Dμ0i2πr(π−1)Consider the circular loop having current I and with central point O. the magnetic field at the central point O is
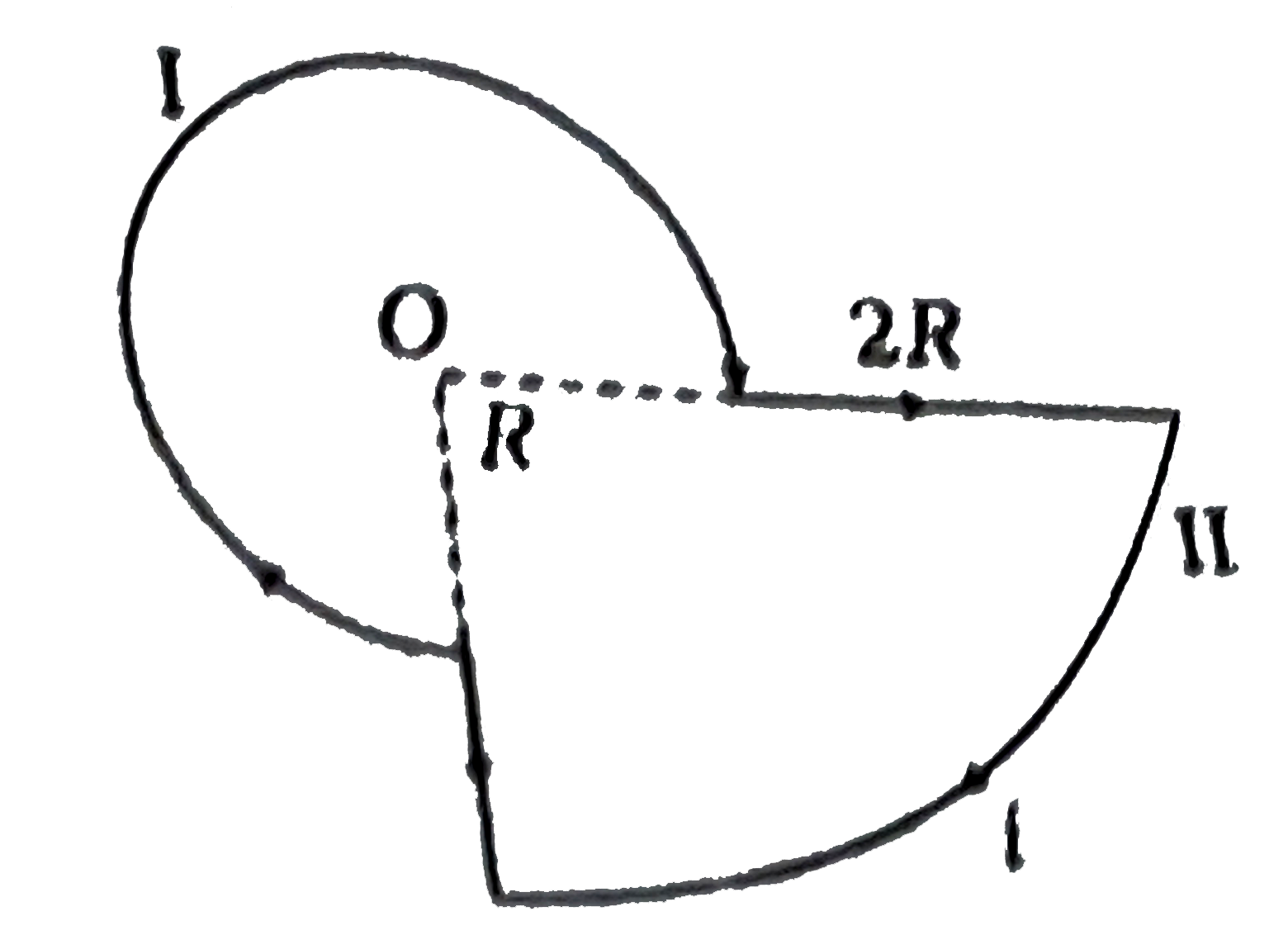 A2μ0i3πR acting downwardB5μ0i12R acting downwardC6μ0i11R acting downwardD3μ0i7R acting downward
A2μ0i3πR acting downwardB5μ0i12R acting downwardC6μ0i11R acting downwardD3μ0i7R acting downward
A current loop, having two circular arcs jo ined by two radial lines is shown in the figure. It carries a current of 10 A. The magnetic field at point O will be close to :
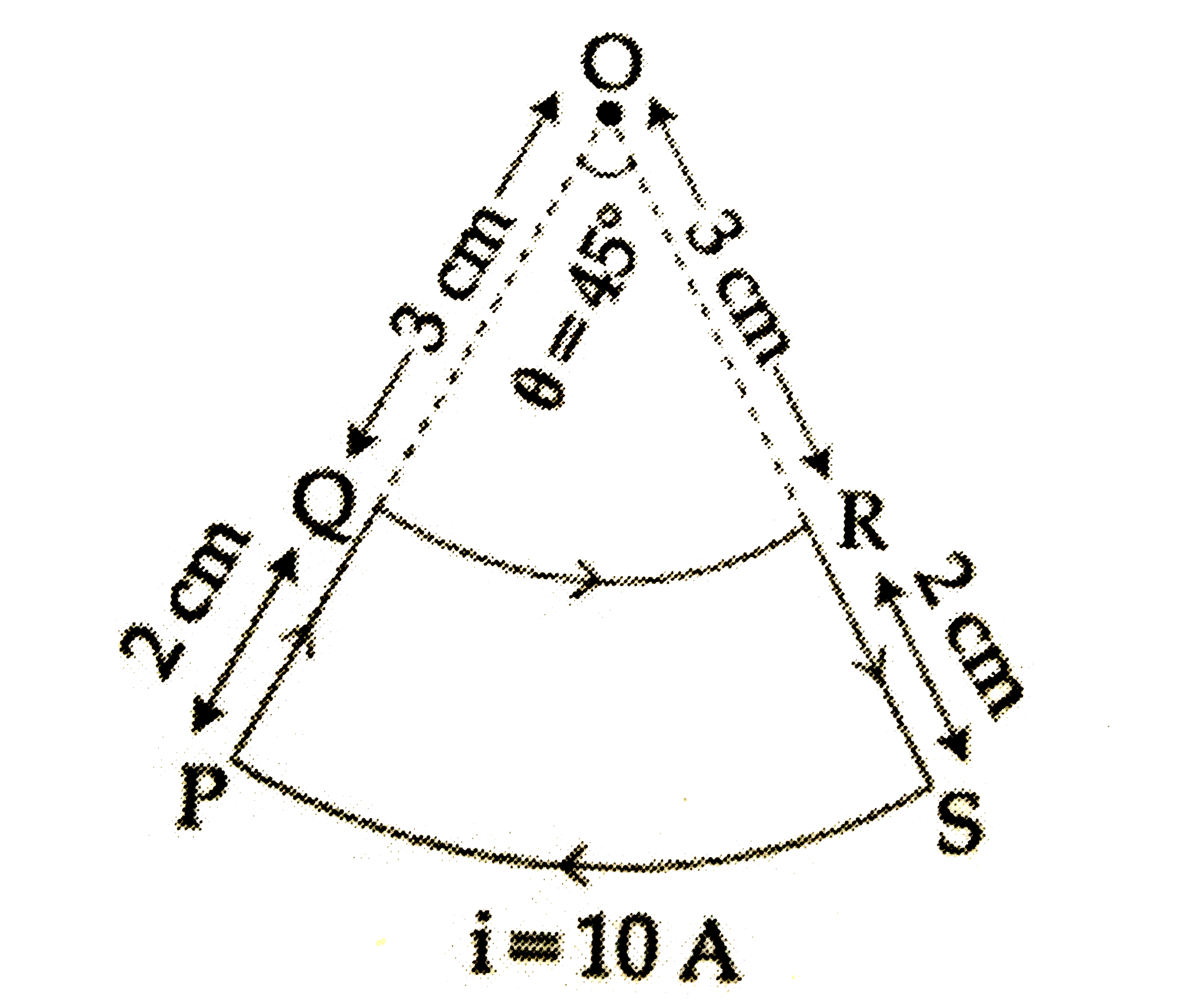
View SolutionUsing Biot-Savart’s law, derive an expression for magnetic field at any point on axial line of a current carrying circular loop. Hence, find magnitude of magnetic field intensity at the centre of circular coil.
View SolutionUsing Biot - Savart's law, derive an expression for magnetic field at any point on axial line of a current carrying circular loop. Hence, find magnitude of magnetic field intensity at the centre of circular coil.
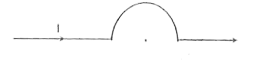
View SolutionAn infinitely long straight conductor is bent into the shape as shown in figure. It carries the current I and radius of the circular loop is a, then the magnetic field at the centre of the loop is ______
View SolutionA conducting circular loop of radius a is connected to two long, straight wires . The straight wires carry a current I as shown in figure . Find the magnetic field B at the centre of the loop.

View Solution
