A charged particle carrying charge q=1μc moves in uniform magnetic with velocity v1=106m/s at angle 45∘ with x-axis in the xy-plane and experiences a force F1=5√2mN along the negative z-axis. When te same particle moves with velocity v2=106m/s along the z-axis it experiences a force F2 in y-direction. Find
a. the magnitude and direction of the magnetic field
b. the magnetic of the force F2.
F2 is in y-direction when velocity is along z-axis. Therfore, magnetic field should be along x-axis. So let,
B=B0ˆi
a. Given, v1=106√2ˆi+106√2ˆj
and F1=−5√2×10−3ˆk
From the equation F=q(v×B)
We have (−5√2×10−3)ˆk=(10−6)[(106√2ˆi+106√2ˆj)×(B0ˆi)]
=−B0√2ˆk
∴B0√2=5√2×10−3
or B0=10−2T
Therefore, the magnetic field is
B=(10−2ˆi)T
b. F2=B0qv2sin90∘
As the angle between B and v in this case is 90∘
∴F2=(10−2)(10−6)(106)
=10−2N
Similar Questions
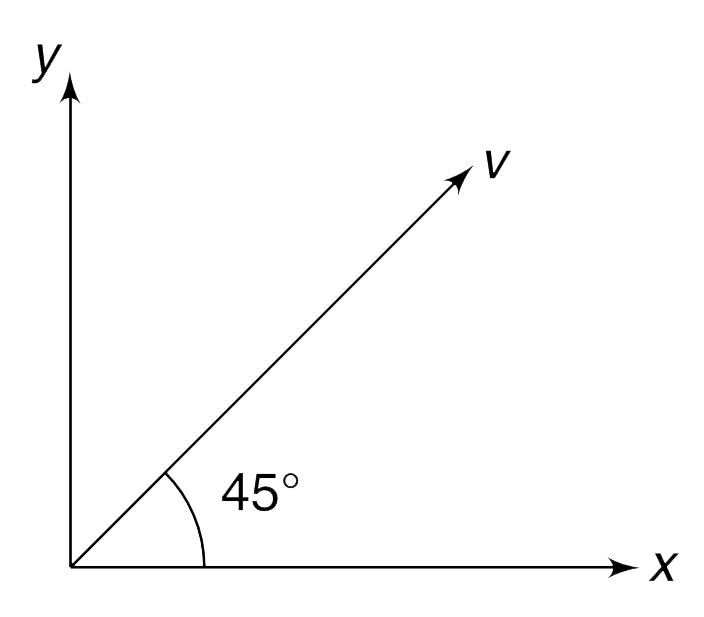
A particle having charge q=10μC is moving with a velocity of V=106m/sin a direction making an angle of 45° with positive x axis in the xy plane (see figure). It expe- riences a magnetic force along negative z direction. When the same particle is projected with a velocity v'=106m/sin positive z direction, it experiences a magnetic force of 10 mN along X direction. Find the direction and magnitude of the magnetic field in the region.
View SolutionA beam of α-particle projected along +x - axis, experiences a force due to a magnetic field along the +y-axis. What is the direction of the magnetic field?
View Solution
Knowledge Check
A charged particle carrying charge q=10μC moves with velocity v1=106,s−1 at angle 45∘ with x-axis in the xy plane and experience a force F1=5√2mN along the negative z-axis. When the same particle moves with velocity v2=106ms−1 along the z-axis, it experiences a force F2 in y-direction.
Find the magnetic field →B.A(10−3T)(ˆi+ˆj)B(2×10−3T)ˆiC(10−3T)ˆiD(2×10−3T)(ˆi+ˆj)A charged particle carrying charge q=10μC moves with velocity v1=106,s−1 at angle 45∘ with x-axis in the xy plane and experience a force F1=5√2mN along the negative z-axis. When the same particle moves with velocity v2=106ms−1 along the z-axis, it experiences a force F2 in y-direction.
Find the magnitude of the force F2.A10−2NB10−3NC10−4ND10−5NThe force acting on a particle of charge q moving in a uniform magnets field with velocity v is
Aparallel to both →v and →BBperpendicular to both →v and →BCparallel to →v and perpendicular to →BDperpendicular to →v and parallel to →B
A beam of α particles projected along + x-axis, experiences a force due to a magnetic field along the +y-axis figure. What is the direction of magnetic field.
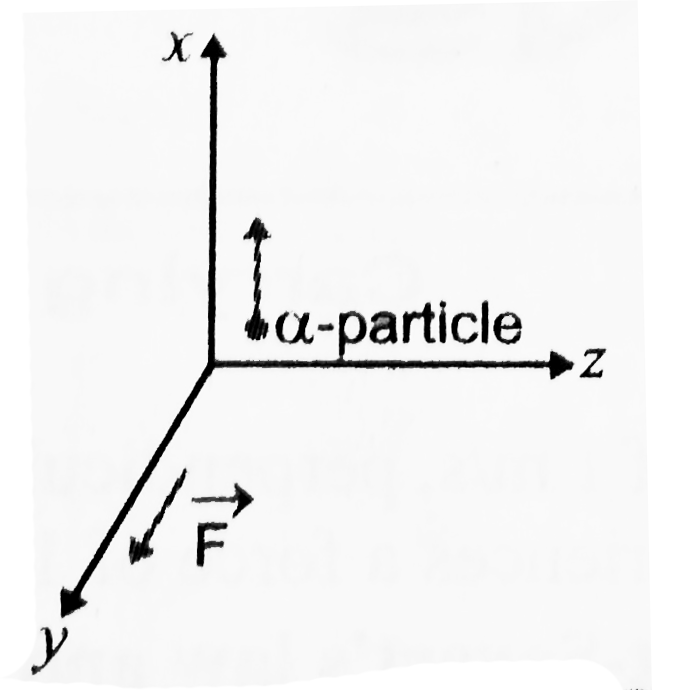
View SolutionWhen a charge of 1C moving with velocity 1 m/s normal to a magnetic field experiences a force 1N, then the magnitude of them magnetic field is.
View SolutionA charge q is moving with a velocity v1=1ˆi m/s at a point in a magentic field and experiences a force F=q[−ˆj+1ˆk] N. If the charge is moving with a voloctiy v2=2ˆj m/s at the same point then it experiences a force F2=q(1ˆi−1ˆk) N. The magnetic induction B at that point is
View SolutionIf particle of charge 10−12 coulomb moving along the ˆx - direction with a velocity 105m/s experiences a force of 10−10 newton in ˆy - direction due to magnetic field, then the minimum magnetic field is
View SolutionIf a particle of charge 10−12 coulomb moving along the ˆx-direction with a velocity 105m/s experiences a force of 10−10 newton in ˆy-direction due to magnetic field. Then the minimum magnetic field is
View Solution

