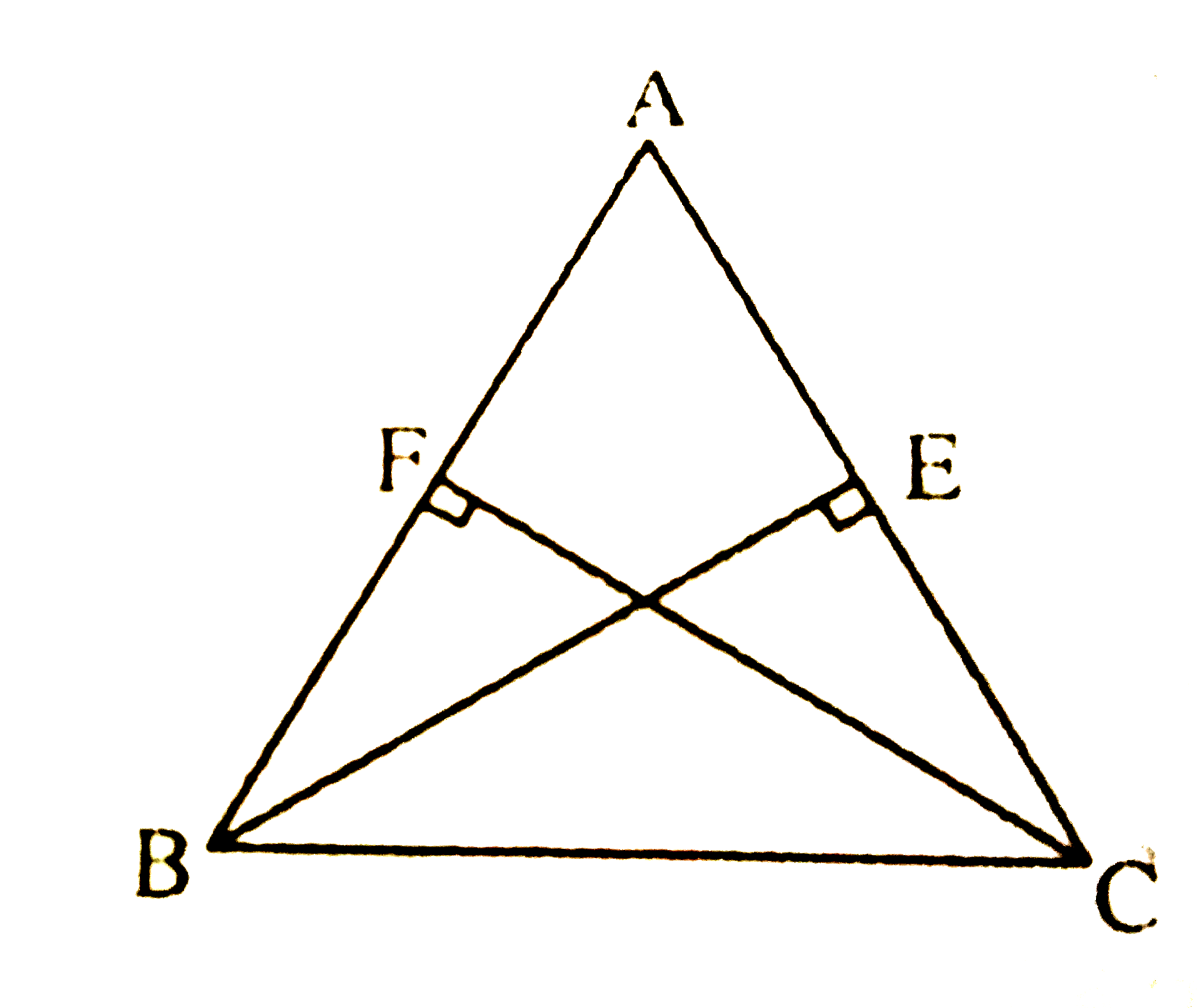
BE और CF एक त्रिभुज ABC के दो बराबर शीर्षलम्ब हैं | RHS सर्वांगसमता नियम का प्रयोग करके सिद्ध कीजिए कि ΔABC एक समद्विबाहु त्रिभुज है |
Video Solution
Text Solution
दिया है : ABC एक त्रिभुज है जिसमें तथा BE⊥AC तथा CF⊥AB तथा BE=CF
सिद्ध करना है कि ΔABC समद्विबाहु है अर्थात AB = AC.
प्रमाण : ΔBEC तथा ΔCFB में,
∠BEC=∠CFB=90∘
BC=BC [उभयनिष्ठ]
तथा BE=CF [दिया है]
अत: ΔBEC≅ΔCFB [RHS सर्वांगसमता नियम से]
∴ ∠ECB=∠FBC
⇒ ∠C=∠B
⇒ AB=AC
|
Similar Questions
दिखाइए कि निम्नलिखित बिंदुओं के समूह एक समद्विबाहु त्रिभुज के शीर्ष हैं :
(1,1), (-1,-1) और (−√3,√3)
View Solutionदिखाइए कि निम्नलिखित बिंदुओं के समूह एक समद्विबाहु त्रिभुज के शीर्ष हैं :
(0,0), (5,5√3) और (−5,5√3)
View Solutionत्रिभुज के शीर्षलम्ब
View Solutionएक त्रिभुज की दो भुजाओं की मापों का योग
View Solutionएक त्रिभुज का क्षेत्रफल
View Solutionयदि दो समकोण त्रिभुजों में से एक त्रिभुज की एक भुजा और एक न्यूनकोण दूसरे त्रिभुज की एक भुजा और तदनुरूपी कोण के बराबर हो, तो दोनों त्रिभुज परस्पर क्या होंगे ?
View SolutionRevision |त्रिभुज का शीर्षलम्ब #!#त्रिभुज का बाह्य कोण
View SolutionRevision |दो विशेष त्रिभुज : समबाहु तथा समद्विबाहु #!#एक त्रिभुज की दो भुजाओं की मापों का योग
View Solution