सिद्ध करें कि दो समरूप त्रिभुजों की परिमाप उनकी भुजाओं के समानुपाती होती है ।
Video Solution
Text Solution
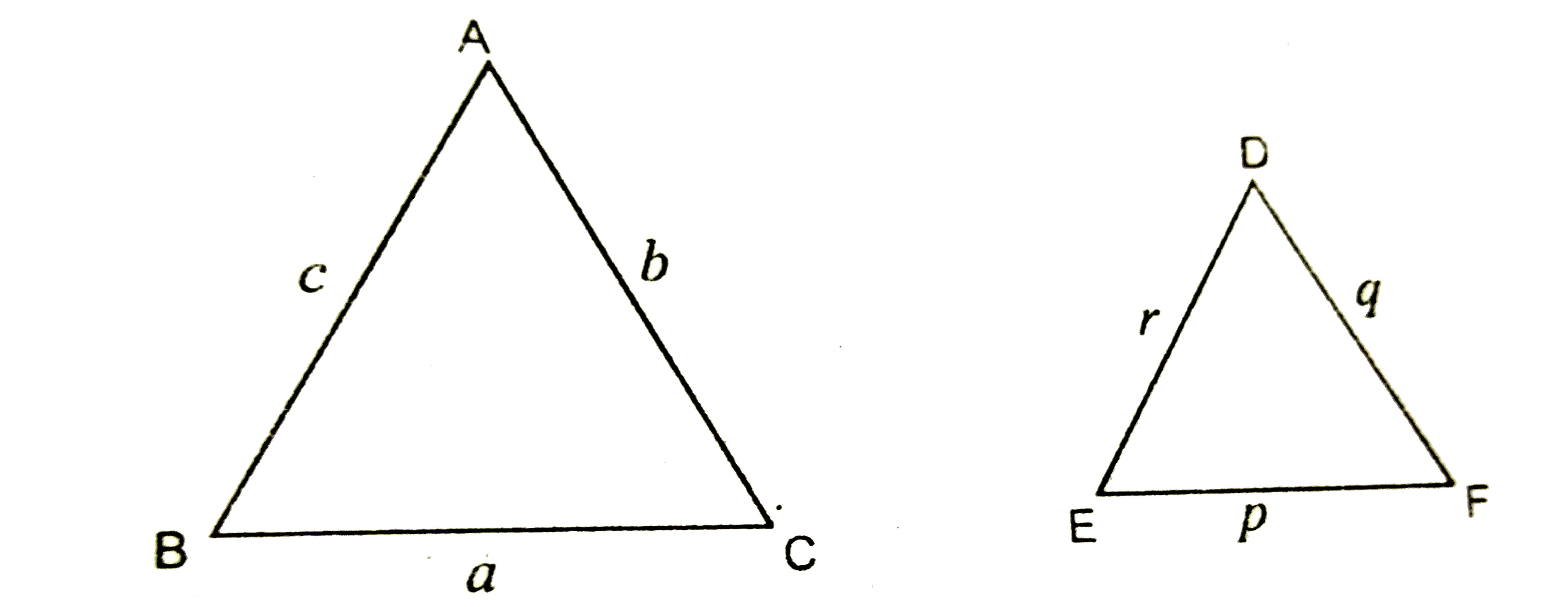
दिया है : ΔABC~ΔDEF
सिद्ध करना है : ΔABCका परिमापΔDEFका परिमाप=ABDE=BCEF=ACDF
उपपत्ति माना कि BC=a,AC=b,AB=c,EF=p,DF=q,DE=r
∵ΔABC~ΔDEF (दिया हुआ है)
अतः उनकी संगत भुजाएँ समानुपाती होंगी ।
∴BCEF=ACDF=ABDE=k (मान लिया)
या ap=bq=cr=k
∴a=pk,b=qk,c=rk
अब ΔABCका परिमापΔDEFका परिमाप=BC+AC+ABEF+DF+DE
=a+b+cp+q+r=pk+qk+rkP+q+r
=k(p+q+r)P+q+r=k
(i) और (iii) से हम पाते है कि,
ΔABCका परिमापΔDEFका परिमाप=ABDE=BCEF=ACDF
|
Similar Questions
त्रिभुज|त्रिभुजों के प्रकार|सर्वांगसम आकृतियाँ|समरूप आकृतियाँ |सारांश
View Solutionबच्चों को कहानी सुनाने की उपयोगिता सिद्ध होती है:
View Solutionसमरूप आकृतियाँ |NCERT प्रश्नावली |त्रिभुजों की समरूपता |सारांश
View SolutionThe perimeters of two similar triangles ABC and PQR are 78 cm and 46.8 cm, respectively. If PQ=11.7, then the length of AB is: दो समरूप त्रिभुजों ABC और PQR के परिमाप क्रमशः 78 सेमी और 46.8 सेमी है। यदि PQ=11.7, तो AB की लंबाई है:
View Solutionत्रिभुजों की समरूपता के लिए कसौटियाँ |समरूप त्रिभुजों का क्षेत्रफल|प्रश्न|सारांश
View Solutionसमरूप त्रिभुजों के क्षेत्रफल|NCERT प्रश्नावली |सारांश
View Solutionसमरूप त्रिभुजों के क्षेत्रफल|NCERT प्रश्नावली |सारांश
View Solutionसमरूप त्रिभुजों का क्षेत्रफल
View Solution