ΔABC में रेखाखण्ड XY∣∣AC है तथा यह AB को X तथा AC को Y पर प्रतिच्छेद करती है और ΔABC को दो समान क्षेत्रफल वाले भाग में विभाजित करती है तो सिद्ध करें कि AXAB=2−√22
एक ΔABC है जिसमे XY∣∣BC इस प्रकार है कि क्षे०(ΔAXY) = क्षे०( समलंब BXYC) सिद्ध करना है : BXAB=2−√22
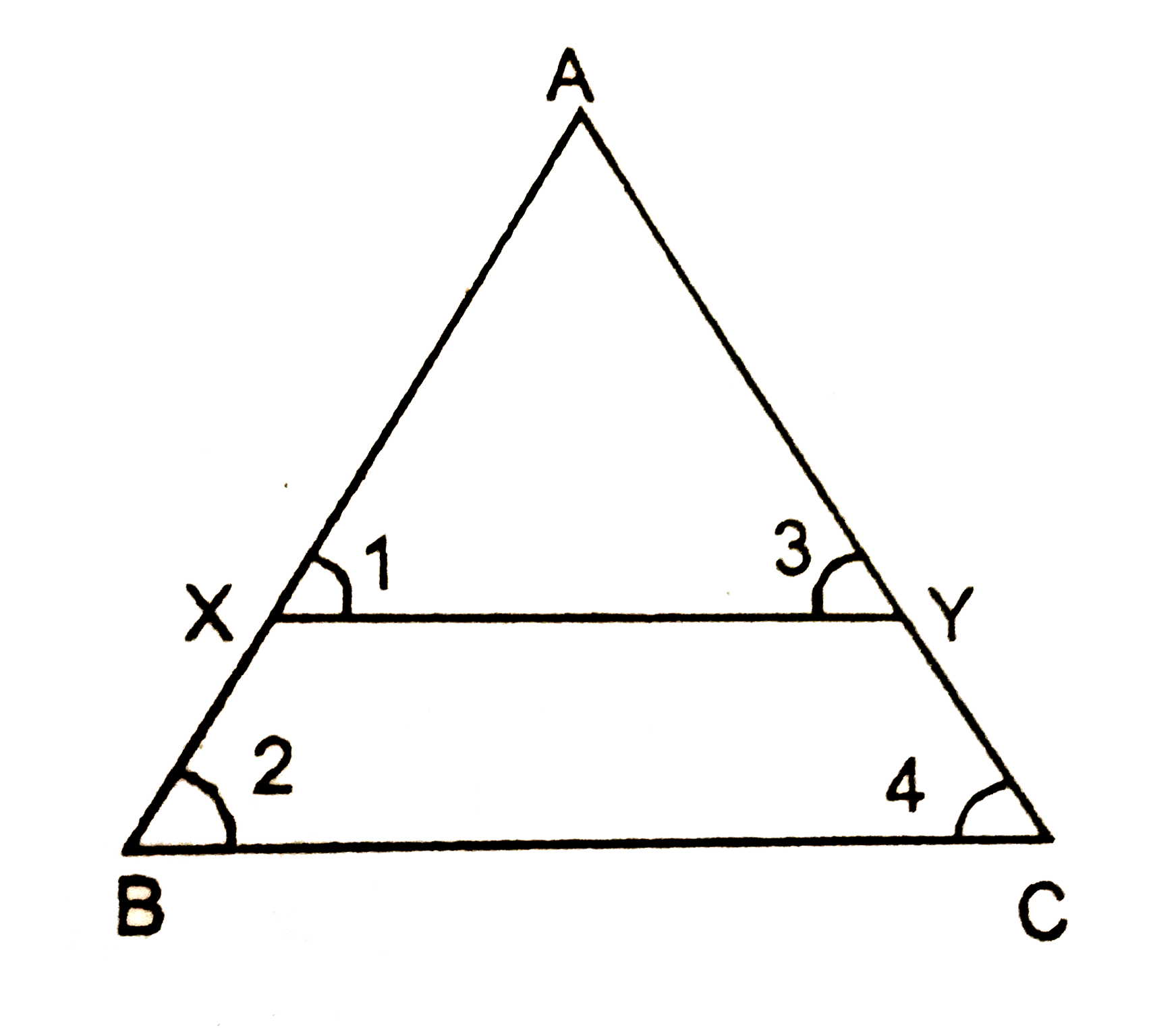
उपपत्ति (प्रमाण) : ΔABC में XY,∣∣BC (दिया है)
अब ΔAXY और ΔABC में,
∠1=∠2
और ∠3=∠4
∴ΔABC~ΔAXY
therefore ("क्षे०"(Delta))/("क्षे०"(DeltaAXY))=(AB^2)/(AX^2)
किन्तु क्षे०(ΔABC)=क्षे०(ΔAXY)+क्षे० (समलंब BXYC)
∴ (i) से हम पाते है कि
क्षे०(ΔAXY)+क्षे०(समलम्बBXYC)क्षे०(ΔAXY)=AB2AX2
∴ (ii) से , क्षे०(ΔAXY)+क्षे०(ΔAXY)क्षे०(ΔAXY)=AB2AX2
⇒2=AB2AX2⇒ABAX=√2
अब, AX=AB−BX
(iii) और (iv) से हम पाते है , AB=√2AX=√2(AB−BX)
⇒√2BX=(√2−1)AB
⇒BXAB=√2−1√2=(√2−1√2)√2√2=2−√22
अतः BXAB=2−√22 (प्रमाणित)
समान प्रश्न
A circle is inscribed in triangle ABC , touching AB at P, BC at Q and AC at R. If AR=5 cm, RC= 6 cm and AB=12 cm, then perimeter of triangle ABC is: एक वृत्त किसी त्रिभुज ABC में समाहित है जो AB को P पर, BC को Q पर तथा AC को R पर स्पर्श करता है | यदि AR =5 सेमी और AB = 12 सेमी है, तो त्रिभुज ABC का परिमाप ज्ञात करें |
View SolutionThe sides AB and AC of a triangle ABC are extended to P and Q respectively. If the bisectors of angle PBC and angle QCB intersect at O, and angle A=92^@ , then angle BOC is equal to: एक त्रिभुज ABC की भुजाओं AB और AC को क्रमशः P तथा Q तक बढ़ाया जाता है | यदि angle PBC तथा angle QCB के समद्विभाजक एक दूसरे को O पर काटते हैं तथा angle A=92^@ है, तो angle BOC किसके बराबर है ?
View SolutionIn triangle ABC , AD bisects angle A and intersects BC at D. If BC = a ,AC = b and AB = c, then BD = ? त्रिभुज ABC में, AD कोण A को समद्विभाजित करता है तथा BC को D पर काटता है | यदि BC = a, AC = b और AB = c है, तो BD = ?
View SolutionIn triangle ABC , D is a point on side AB, such that, BD = 2cm and DA = 3cm. E is a point on BC such that DE || AC and AC = 4 cm. Then (Area of triangle BDE ): (Area of trapezium ACED) is: त्रिभुज ABC में, D, भुजा AB पर स्थित ऐसा बिंदु है कि BD = 2 सेमी और DA =3 सेमी है | E, BC पर स्थित ऐसा बिंदु है कि DE || AC है और AC =4 सेमी है | तो त्रिभुज (BDE का क्षेत्रफल ) : (समलम्ब ACED का क्षेत्रफल) ज्ञात करें |
View SolutionIt is given that triangle ABC ~ triangle PRQ and that Area ABC : Area PRQ = 16: 169. If AB = x, AC = y, BC = z (all in cm), then PQ is equal to: यह दिया गया है कि triangle ABC ~ triangle PRQ है तथा ABC का क्षेत्रफल : PRQ का क्षेत्रफल =16 :169 @ | यदि AB =x, AC =y, BC =z ( सभी सेमी में ) है, तो PQ का मान क्या होगा ?
View SolutionIn triangle ABC ,AD bisects angle A which meets BC at D. If BC = a, AC = b and AB = c, then DC = ? त्रिभुज ABC में, AD कोण A को द्विभाजित करता है जो BC से D पर मिलता है | यदि BC = a, AC = bऔर AB = c है, तो DC = ?
View SolutionIn triangle ABC, D and E are two points on the sides AB and AC respectively so that DE || BC and AD/BD =3/4 .The ratio of the area of △ABC to the area of trapezium DECB is :
त्रिभुज ABC में,D और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु है कि DE ||BC है और AD/BD =3/4 है | त्रिभुज ABC के क्षेत्रफल तथा समलम्ब DECB के क्षेत्रफल में अनुपात ज्ञात करें |
View SolutionIn triangle ABC, D and E are two points on the sides AB and AC respectively so that DE || BC and AD/BD =5/6 .The ratio of the area of △ABC to the area of trapezium DECB is :
त्रिभुज ABC में,D और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु है कि DE ||BC है और AD/BD =5/6 है | त्रिभुज ABC के क्षेत्रफल तथा समलम्ब DECB के क्षेत्रफल के बीच अनुपात ज्ञात करें |
View Solution
