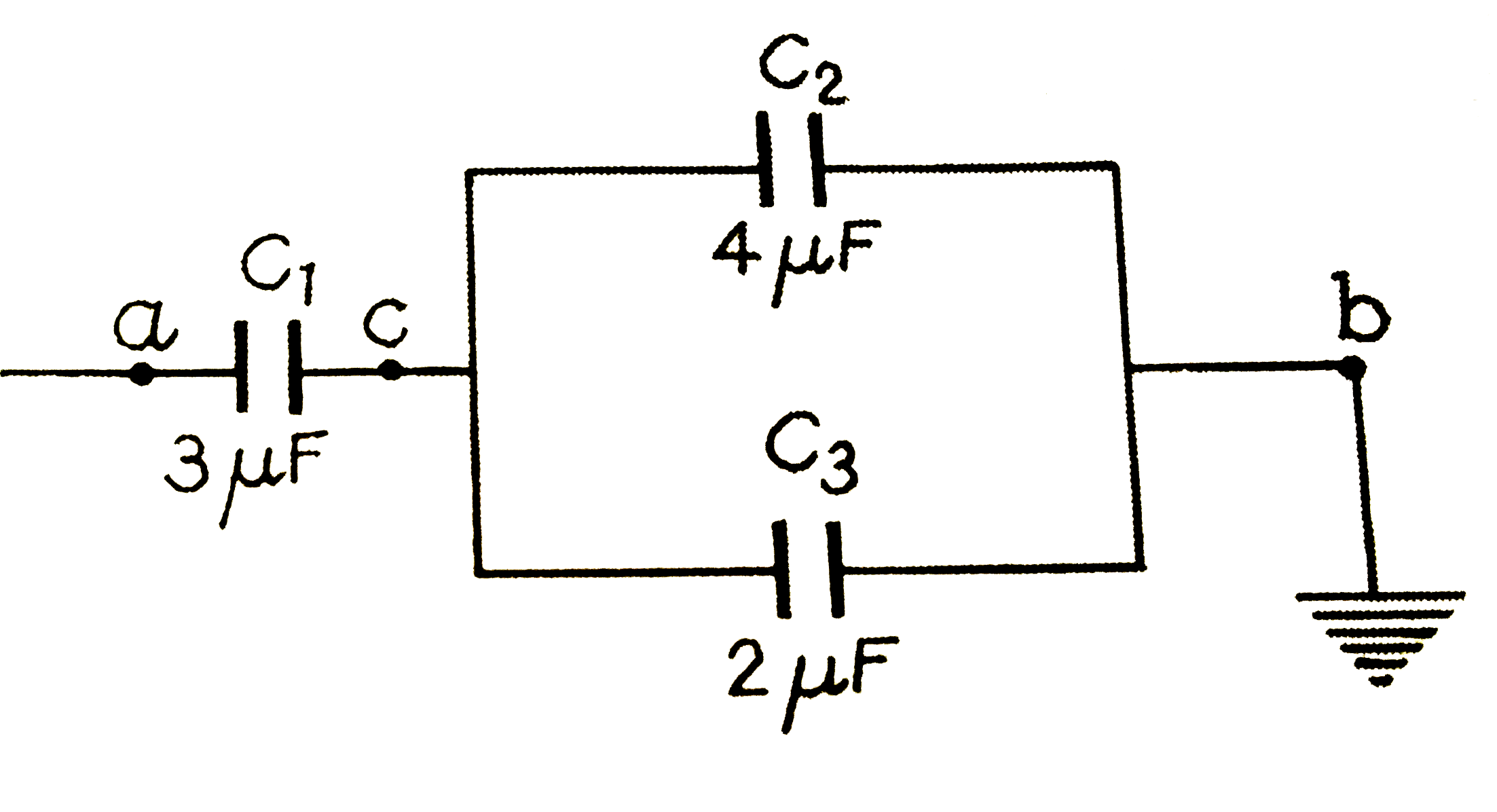
संलग्न चित्र में प्रदर्शित परिपथ में, यदि बिन्दु b को पृथ्वी से सम्बन्धित कर दिया जाये तथा बिन्दु a को + 1200 वोल्ट विभव पर रखा जाये तो प्रत्येक संधारित्र पर आवेश तथा बिन्दु c पर विभव की गणना कीजिए ।
A
400 वोल्ट और 0.8×10−3 कूलॉम
B
800 वोल्ट और 0.8×10−3 कूलॉम
C
800 वोल्ट और 0.82×10−3 कूलॉम
D
400 वोल्ट और 0.82×10−3 कूलॉम
Video Solution
Text Solution
The correct Answer is:A
संधारित्र C2 व C3 समान्तर - क्रम में जुड़े हैं । अतः इनकी तुल्य - धारिता
C'=C2+C3=4μF+2μF=6μF.
संधारित्र C1 तथा तुल्य - संधारित्र C' श्रेणीक्रम में जुड़े हैं । अतः यदि पुरे परिपथ की तुल्य - धारिता C है तो
C=C1×C'C1+C'=3μF×6μF3μF+6μF=2μF (माइक्रोफैरड)
बिंदुओं a व b के बीच विभवान्तर, Vab=1200 वोल्ट ।
∴ संधारित्रों के पूरे संयोग पर आवेश
q=CVab=(2×10−6फैरड)×(1200 वोल्ट)
=2.4×10−3 कूलॉम |
यही आवेश C1 पर होगा तथा इतना ही आवेश C2 व C3 दोनों पर मिलकर होगा ।
अतः q1=2.4×10−3 कूलॉम ।
अब Vac=q1C1=2.4×10−3कूलॉम3×10−6फैरड=800 वोल्ट |
∴Vac=Va−Vc
∴ बिन्दु C पर विभव Vc=Va−Vac
= 1200 वोल्ट - 800 वोल्ट
= 400 वोल्ट
अब Vcb=Vc−Vb=400 वोल्ट - 0 = 400 वोल्ट ।
∴ प्रत्येक संधारित्र पर आवेश
q2=C2Vcb=(4×10−6फैरड)×(400वोल्ट)
=1.6×10−3 कूलॉम |
तथा q3=C3Vcb=(2×10−6फैरड)×(400वोल्ट)
=0.8×10−3 कूलॉम |
|
Similar Questions
Board Special |विद्युत द्विध्रुव के कारण किसी बिन्दु पर विभव पर आँकिक प्रश्न
View Solutionतीन प्रतिरोधों 2Ω,4Ω,5Ω को श्रेणीक्रम में जोड़ा जाता है तथा इस संयोजन को 12 V वि.वा.बल एवं नगण्य आन्तरिक प्रतिरोध की एक बैटरी से जोड़ा गया है। इन प्रतिरोधों में विभव बिन्दु हैं
View SolutionRecap|एक बिन्दु आवेश के कारण विभव |आवेश के निकाय के कारण वेधयुत विभव |दो बिन्दुओ के बीच विभवांतर |Summary
View SolutionRecap|वैधुत द्विध्रुव के कारण किसी बिन्दु पर विभव |Question|OMR|Summary
View Solutionफलन की बिन्दु पर सततता
View Solutionमध्य बिन्दु प्रमेय पर प्रश्न
View Solutionफलन की बिन्दु पर सततता #!#अभ्यास प्रश्न
View Solutionएक बिन्दु से एक वृत्त पर स्पर्श रेखाओं की संख्या
View Solution

