प्रथम चतुर्थेाश में वृत्त x2+y2=4 एव रेखाओ x=0,x=2 से घिरे क्षेत्र का क्षेत्रफल है:
A
π
B
π2
C
π3
D
π4
वीडियो समाधान
लिखित उत्तर
वृत्त तथा रेखाओ x = 0 एव x =2 के द्वारा प्रथम चतुर्थेाश में घिरे क्षेत्रफल को आकृति में छायांकित द्वारा दर्शाया गया है।
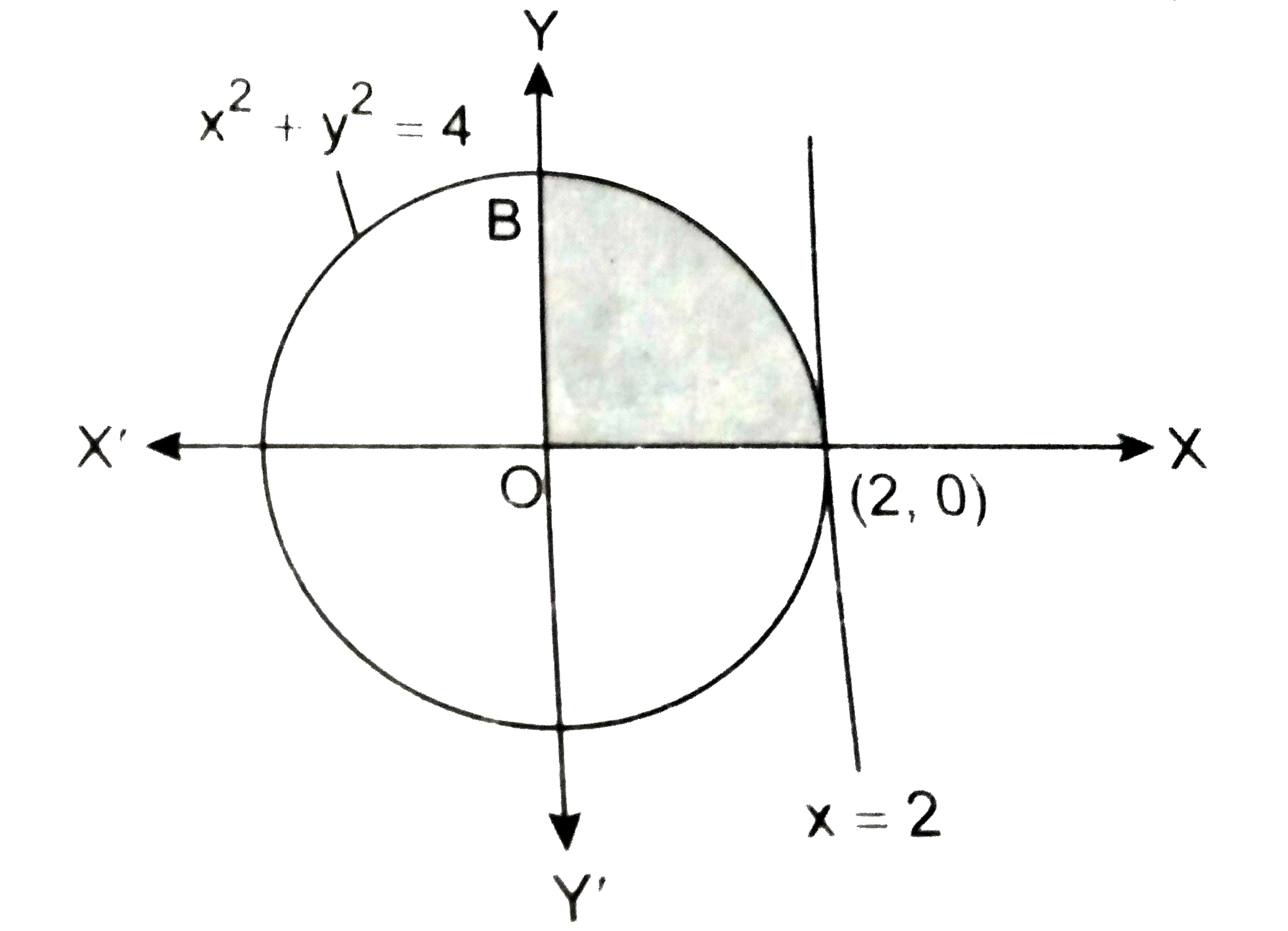
∴ अभीष्ट क्षेत्रफल =∫20ydx=∫20√4−x2dx
=[x2√4−x2+42sin−1(x2)]20
=0+2sin−1(1)−0
=2×π2=πवर्ग इकाई ।
|
समान प्रश्न
वृत्त x2+y2=16 तथा परवलय x2=6y से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solutionवृत्त x2+y2=9 तथा (x−3)2+y2=9 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solutiony2=16−x2 तथा y = 0, x = 0 से प्रथम चतुर्थांश में घिरे क्षेत्र का क्षेत्रफल (वर्ग इकाई में ) है-
View Solutionवक्र y=mx, x-अक्ष एवं कोटियों x=0 तथा x=4 से परिबद्ध क्षेत्र का क्षेत्रफल लिखिए।
View Solutionयदि वक्रो y=kx2 तथा x=ky2,(k>0) के बीच घिरे क्षेत्र का क्षेत्रफल 1 वर्ग इकाई है, तो k बराबर है
View Solutionपरवलय y=x2+2 तथा y=x+1,x=0 रेखाओ x=3 ओर द्वारा घिरे हुए क्षेत्र का क्षेत्रफल (वर्ग इकाइयो में) है
View Solutionवक्र y=ex,y=e−x तथा सरल रेखा x=1 के बीच घिरे क्षेत्र का क्षेत्रफल है।
View Solutionx=a ,x=b ,y=f(x) तथा x - अक्ष से घिरे क्षेत्र का क्षेत्रफल
View Solution

