सदिश विधि द्वारा सिद्ध कीजिए कि sin(α−β)=sinαcosβ−cosαsinβ
Video Solution
Text Solution
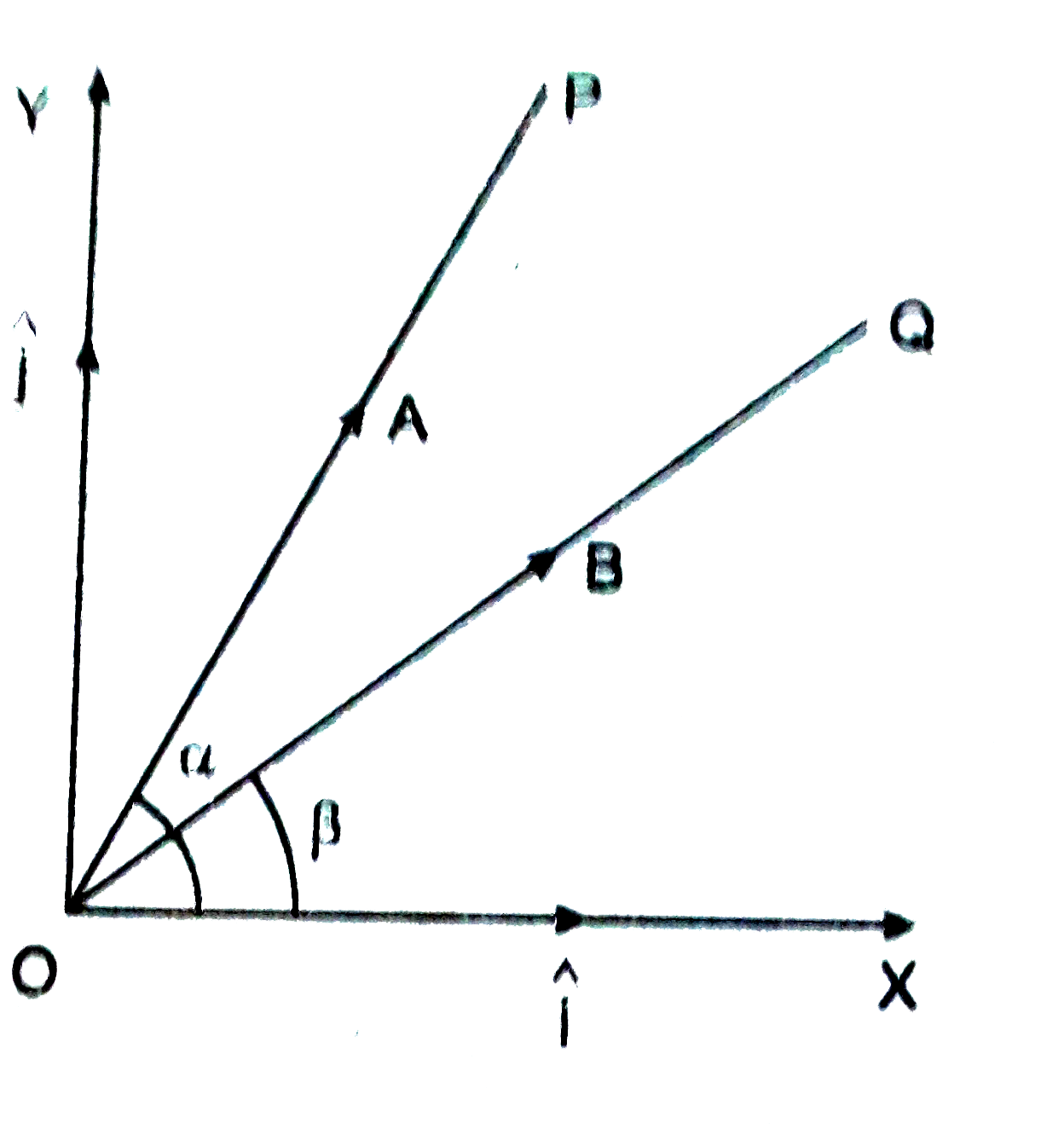
माना ˆi और ˆj क्रमश : OX और OY दिशा में एकांक सदिश है OP और OQ रेखाएँxy - समतल में स्थित है जो OX से क्रमश : α और β कोण बनती है
∴∠POQ=α−β
यदि OP दिशा में एकांक सदिश −−→OA है , तो
−−→OA=cosα.ˆi+sinα.ˆj
इसी प्रकार यदि OQ दिशा में एकांक सदिश −−→OB है तो
−−→OB=cosβ.ˆi+sinβ.ˆj
∴−−→OB×−−→OA=(cosβ.ˆi+sinβ.ˆj)×(cosα.ˆi+sinα.ˆj)
=∣∣∣(ˆi,ˆj,ˆk),cosβ,sinβ,0cosα,sinα,0∣∣∣
=(sinα.cosβ−cosαsinβ)ˆk .... (1)
सदिश गुणन की परिभाषा से
−−→OB×−−→OA=∣∣∣−−→OB∣∣∣∣∣∣−−→OA∣∣∣sin(α−β).ˆk
=1×1×sin(α−β).ˆk
=sin(α−β).ˆk
∴ समीकरण (1) और (2) से
sin(α−β).ˆk=(sinαcosβ−cosαsinβ).ˆk
⇒sin(α−β)=sinαcosβ−cosαsinβ
|
Similar Questions
यदि A=[cosαsinαsinαcosα] तथा B=[cosβsinβsinβcosβ] तो सिद्ध कीजिए कि AB=BA.
View SolutionEvaluate ⎡⎢⎣cosαcosβcosαsinβ−sinα−sinβcosβ0sinαcosβsinαsinβcosα⎤⎥⎦=0
View SolutionEvaluate ∣(cosαcosβ,cosαsinβ,−sinα),(−sinβ,cosβ,0),(sinαcosβ,sinαsinβ,cosα)|}=0
View SolutionEvaluate ∣(cosαcosβ,cosαsinβ,−sinα),(−sinβ,cosβ,0),(sinαcosβ,sinαsinβ,cosα)|}=1
View SolutionEvaluate ⎡⎢⎣cosαcosβcosαsinβ−sinα−sinβcosβ0sinαcosβsinαsinβcosα⎤⎥⎦=0
View SolutionIf Δ=∣∣ ∣ ∣∣sinαcosαsinα+cosβsinβcosαsinβ+cosβsinγcosαsinγ+cosβ∣∣ ∣ ∣∣ then Δ equals
View Solution(i) sin(α+β)=sinαcosβ+cosαsinβ)
(ii) sin(α−β)=sinαcosβ−cosαsinβ
Proof
View SolutionEvaluate ∣∣ ∣ ∣∣cosαcosβcosαsinβ−sinα−sinβcosβ0sinαcosβsinαsinβcosα∣∣ ∣ ∣∣
View Solution
