E व F क्रमशः समतल चतुर्भुज ABCD की असमान्तर भुजाओं के मध्य बिन्दु है। सिद्ध कीजिए की
(i) EF∣∣AB
(ii)EF=12(AB+CD)
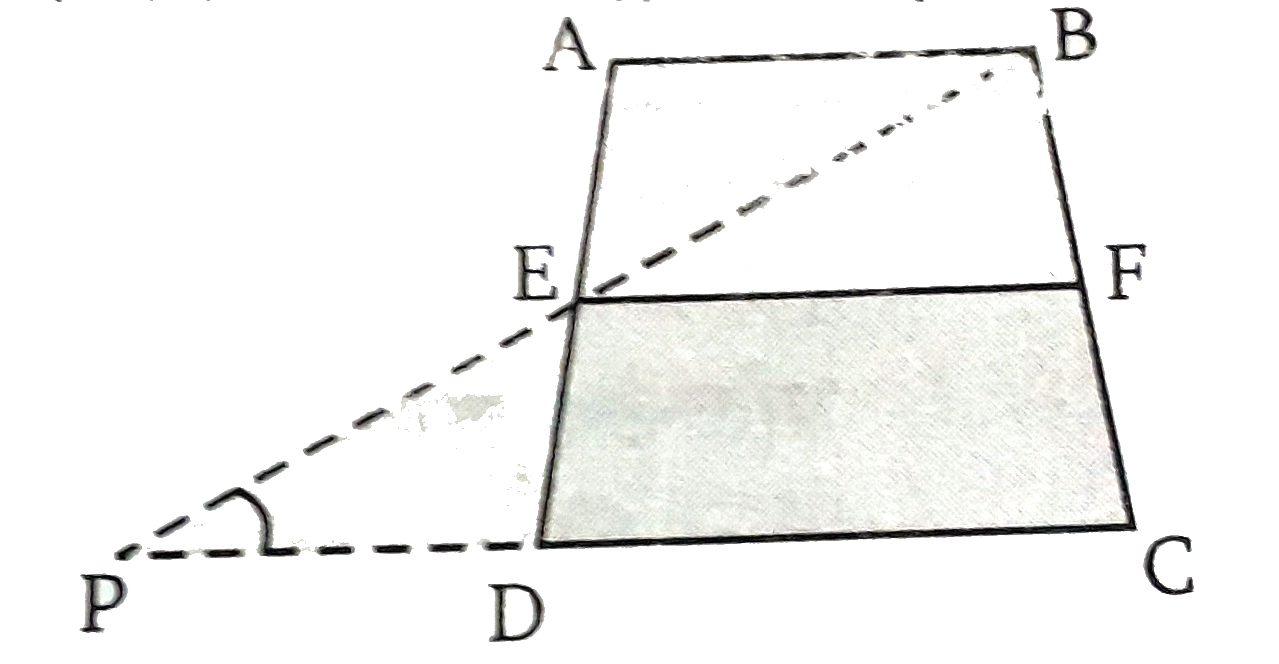
B व E को मिलाये तथा इसे इतना बढ़ाये की यह बिन्दु P पर CD से मिले
त्रिभुज AEB व DEP में,
AE=ED<br>[∴E,AD का मध्य बिन्दु है]
∠ABE=∠EPD (एकान्तर कोण)
[ ∴AB∣∣PC व तिर्यक रेखा BP,B व P पर इनसे मिलती है।]
∠AEB=∠PED
∴ΔAEB≅ΔDEP
[शीर्षाभिमुख कोण]
⇒BE=PE
[CPCT] ....(1)
व AB=DP
[CPCT] ....(2)
अब ΔBPC में E व F क्रमशः BP व BC के मध्य बिन्दु है।
∴EF∣∣PC व EF=12PC
अथार्त EF∣∣AB व EF=12(PD+DC)
=12(AB+DC)
[ समीकरण (2) से]
अतः EF∣∣AB व EF=12(AB+DC)
Similar Questions
The inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionIn the given figure, PQRS is a parallelogram. A and B are the mid-point of ¯¯¯¯¯¯PQ and ¯¯¯¯¯SR respectively. If PS=BR, then the quadrilateral ADBC is a…………………… ,
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E05_020_Q01.png" width="80%"gt
View SolutionIn the figure (not to scale) AB = AC and BD = CD. Find ∠ADB
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C15_E05_003_Q01.png" width="80%"gt
View SolutionMatch the followings (column I with column II)
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C03_E01_011_Q01.png" width="80%"gt
View SolutionMatch column I with column II
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C16_E01_002_Q01.png" width="80%"gt
View SolutionMatch column I with column II:
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C18_E01_003_Q01.png" width="80%"gt
View Solution
