संलग्न चित्र में एक समांतर चतुर्भुज ABCD है तथा BC पर कोई बिंदु P है तो सिद्ध कीजिए कि:
(ΔABP) का क्षे0 +(ΔDPC) का क्षे0 =(ΔPDA) का क्षे0
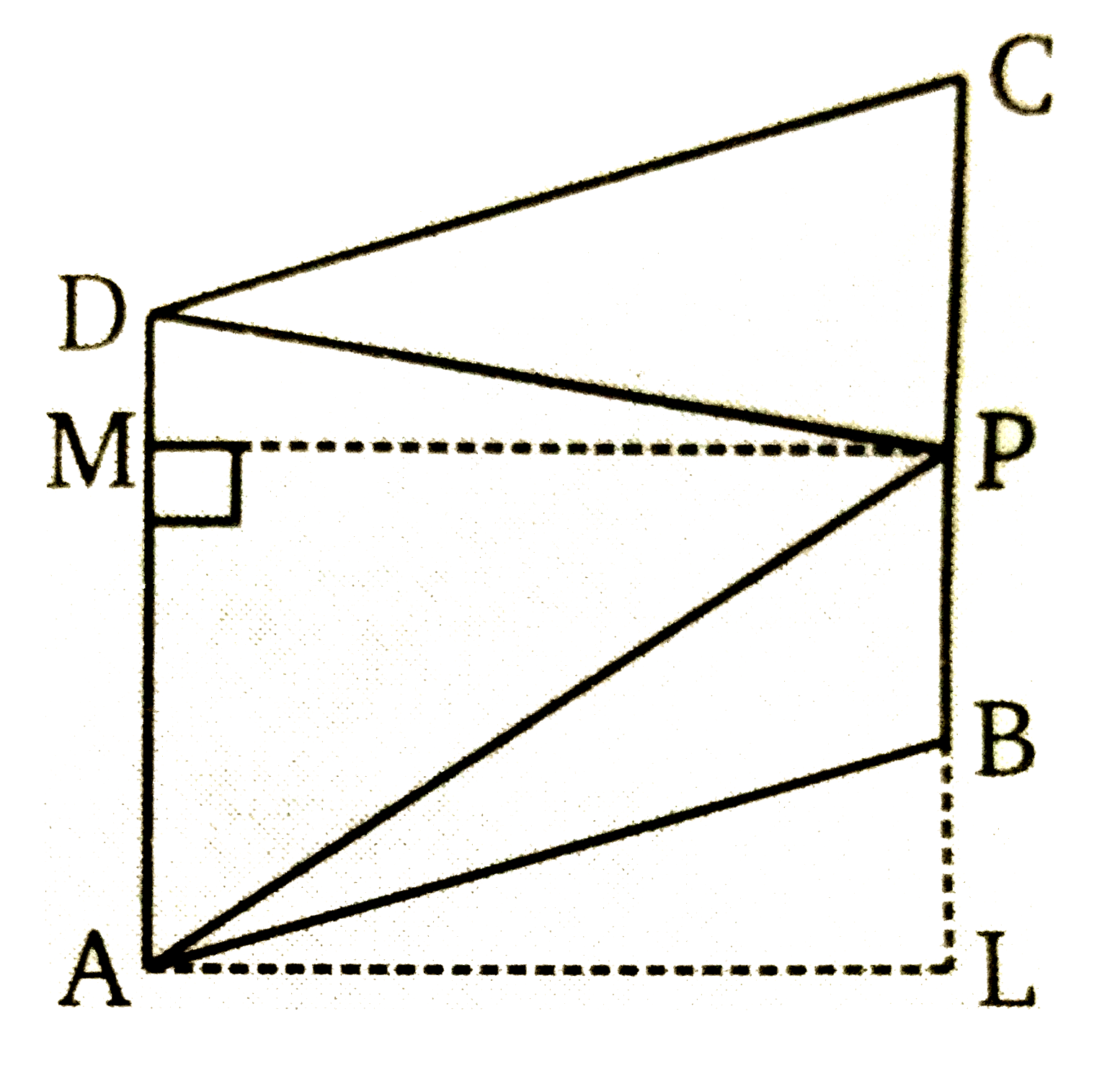
चित्र में दिखाये अनुसार AL⊥BC तथा PM⊥AD खींची।
अब चूंकि BC∣∣AD इसलिए इनके बीच की दूरी भी समान हैं।
इसलिए AL=PM
अब (ΔABP) का क्षे0 +(ΔDPC) का क्षे0
=12×BP×AL+12×PC×AL
=12×AL×(BP+PC)=12×AL×BC
=12PM×AD=(ΔPDA) का क्षे0 (∵AL=PM तथा BC=AD)
Topper's Solved these Questions
- समांतर चतुर्भुज व त्रिभुज के क्षेत्रफलBook:BALAJI PUBLICATIONChapter:समांतर चतुर्भुज व त्रिभुज के क्षेत्रफलExercise:अति लघु उत्तरीय प्रश्न
Explore 5 Videos
- समांतर चतुर्भुज व त्रिभुज के क्षेत्रफलBook:BALAJI PUBLICATIONChapter:समांतर चतुर्भुज व त्रिभुज के क्षेत्रफलExercise:लघु उत्तरीय प्रश्न
Explore 16 Videos
- शेषफल प्रमेय तथा गुणनखण्ड प्रमेय Book:BALAJI PUBLICATIONChapter:शेषफल प्रमेय तथा गुणनखण्ड प्रमेय Exercise:स्वमूल्यांकन परिक्षण
Explore 20 Videos
- सांख्यिकीBook:BALAJI PUBLICATIONChapter:सांख्यिकीExercise:स्वमूल्यांकन परीक्षण
Explore 17 Videos
Similar Questions
एक समांतर चतुर्भुज के विकर्ण इसे कितने भागों में विभक्त करते हैं?
View Solutionचित्र (i) और (ii) में दिए गये समलम्ब चतुर्भुजों ABCD और PQRS का क्षेत्रफल ज्ञात कीजिए।

View Solutionx3+3x2+3x+1 को 5+2x से भाग करने पर शेषफल ज्ञात कीजिए।
View Solutionतीन सिक्के 30 बार उछाले गये। प्रत्येक बार आये चित् की संख्या निम्न प्रकार लिखी गयी :
0,1,2,2,1,2,3,1,3,0,1,3,1,1,2,2,0,1,2,1,3,0,0,1,1,2,3,2,2,0
उपरोक्त आँकड़ों के लिए एक बारंबारता बंटन सारणी तैयार कीजिए।
View SolutionHow many lines of symmetry does the above figure have ?
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionWhich inequations represent the shaded region in the given figure
View SolutionAt point P, the value of (dy)/(dx) is : ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R04_E01_025_Q01.png" width="80%"gt
View Solution