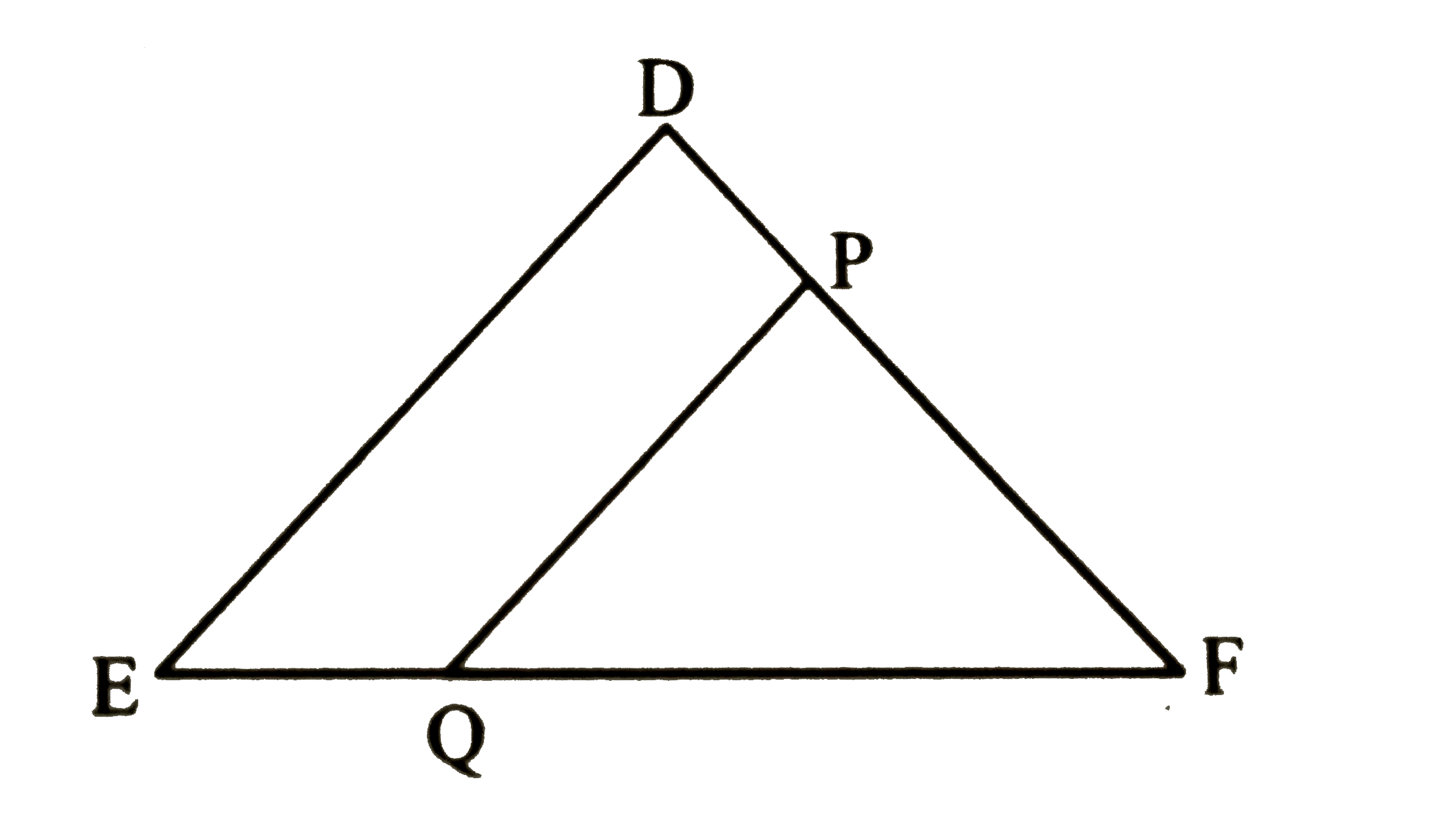
In the figure seg PQ∣∣ seg DE, A(ΔPQF)=20 units PF=2DP,then find A(□DPQE) by completing the following activity:
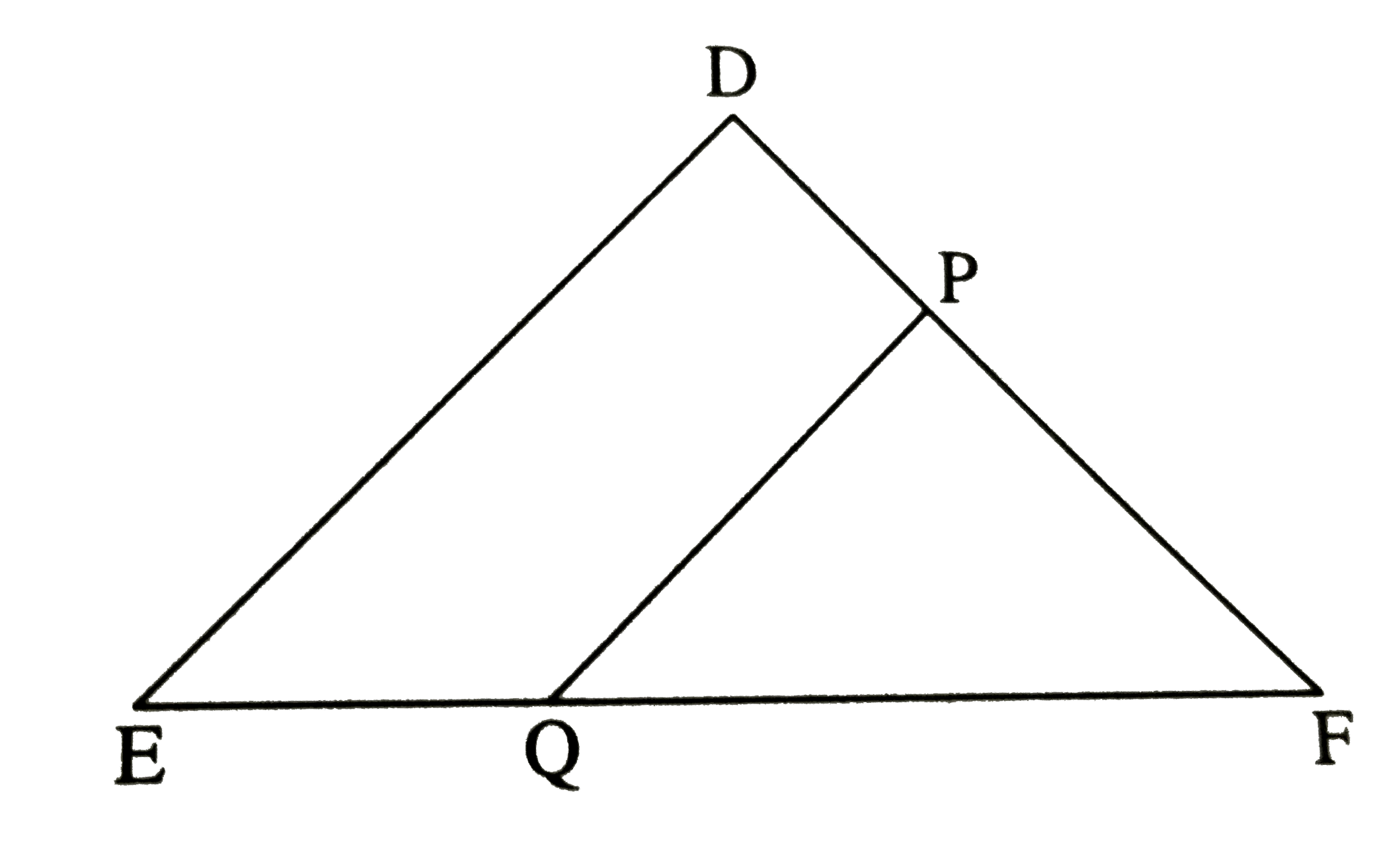
Activity: A(ΔPQF)=20 sq units, PF=2DP.
Let us assume DP=x
∴PF=2x
DF=DE+□=□+□=3x
In ΔFDE and ΔFPQ.
∠FDE≅∠□ ..........(Corresponding angles)
∠FED≅∠□ .....(Corresponding angles)
∴ΔFDE~ΔFPQ .....(AA test)
∴A(ΔFDE)A(ΔFPQ)=□□=(3x)2(2x)2=94
A(ΔFDE)=94A(ΔFPQ)=94×□=□
A(□DPQE)=A(ΔFDE)−A(ΔFPQ)
=□−□
=□
A(ΔPQF)=20 sq units, PF=2DP.
Let us assume DP=x
∴PF=2x
DF=DP+PF=x+2x=3x
In ΔFDE and ΔFPQ
∠Fde≅∠FPQ ……(Corresponding angles)
∠FED≅∠FQP …..(Corresponding angles)
∴ΔFDE~ΔFPQ ...(AA test)
∴A(ΔFDE)A(ΔFPQ)=DF2PF2=(3x2)(2x)2=94
A(ΔFDE)=94A(ΔFPQ)=94×20=45 sq units
A(□DPQE)=A(ΔFDE)−A(ΔFPQ)
=45−20
=25 sq units.
Topper's Solved these Questions
- SIMILARITYBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:SIMILARITYExercise:CHALLENGING QUESTIONS
Explore 8 Videos
- SIMILARITYBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:SIMILARITYExercise:MCQ TYPE
Explore 15 Videos
- SIMILARITYBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:SIMILARITYExercise:2.5 (4 mark each)
Explore 3 Videos
- QUADRATIC EQUATIONS Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:QUADRATIC EQUATIONS Exercise:ASSIGNEMENT 2.4
Explore 8 Videos
- STATISTICSBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:STATISTICSExercise:EXAMPLES FOR PRACTICE (MCQs)
Explore 35 Videos
Similar Questions
Knowledge Check
The square root of x4−2x2+1
A(x+1)(x−1)B(x+1)(x−2)Cx2+1Dnone of these
If ΔABC~ΔPQR and AB:PQ=2:3, then fill in the blanks:
A(ΔABC)A(ΔPQR)=(AB)2□=2232=□□
A(ΔABC)A(ΔPQR)=AB2PQ2=2232=49
View SolutionSolve the following equations by completing the square :
(x−1)(x−2)=20
View SolutionSolve the following equations by completing the square :
x2−2x=15
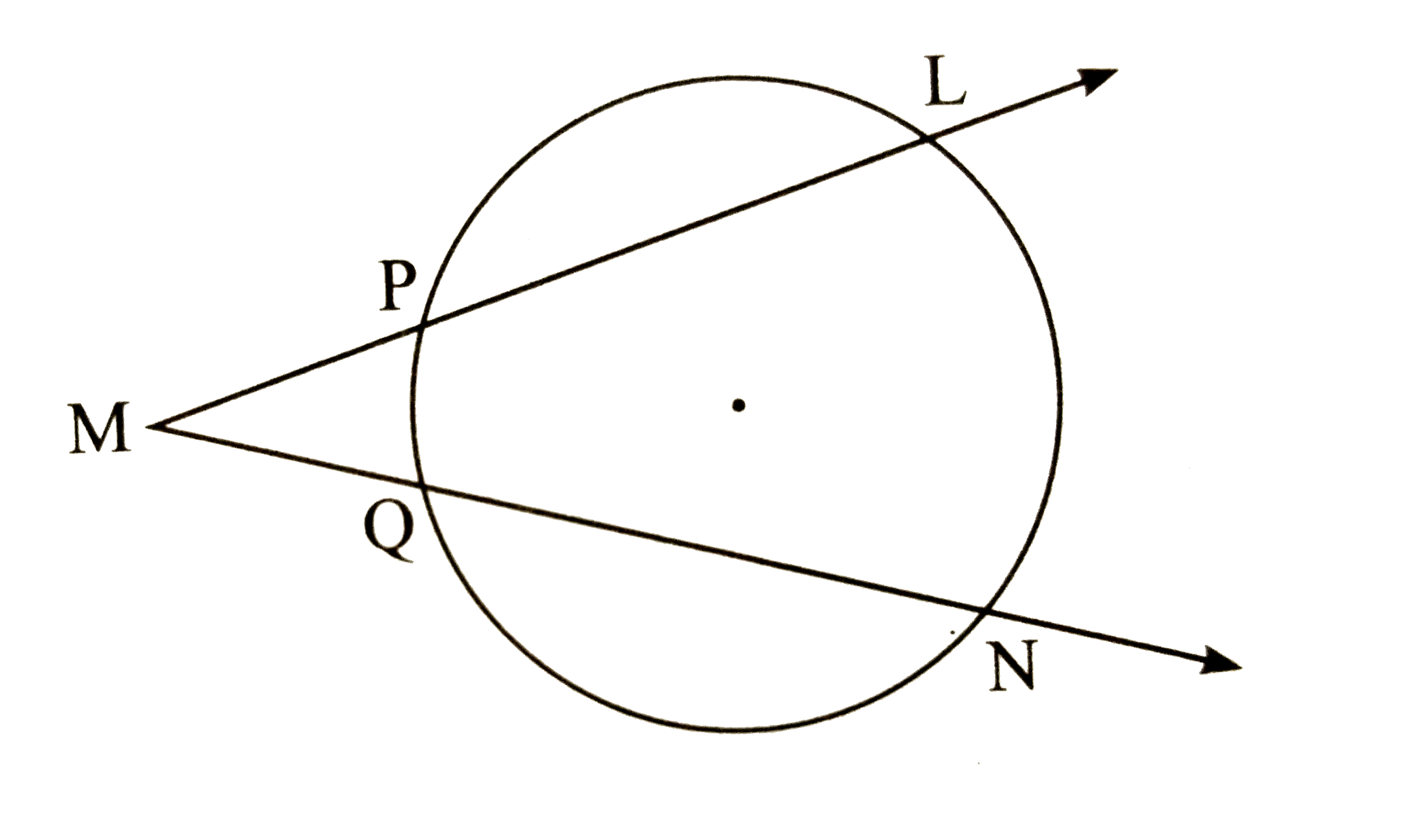
View SolutionIn the figure, m (arc LN ) =110∘, m ( ar PQ ) = 50∘ then complete the following activity to find ∠LMN
∠LMN=12[m(arcLN)=−□]
∴∠LMN=12[□−50∘]
∴_LMN=12×□
∴∠LMN=□
View SolutionComplete the following:
2x+y=8
x: 0, □, 3
y: □, 4, 2
(x,y): □, □, (3,2)
x−y=1
x: □, 2, □
y: -1, □, 4
(x,y): □, □, □
View SolutionIn the figure, ∠DFE=90∘, seg FG⊥ side DE, DG=8, FG=12 then complete the following activity to find the length of seg DE.
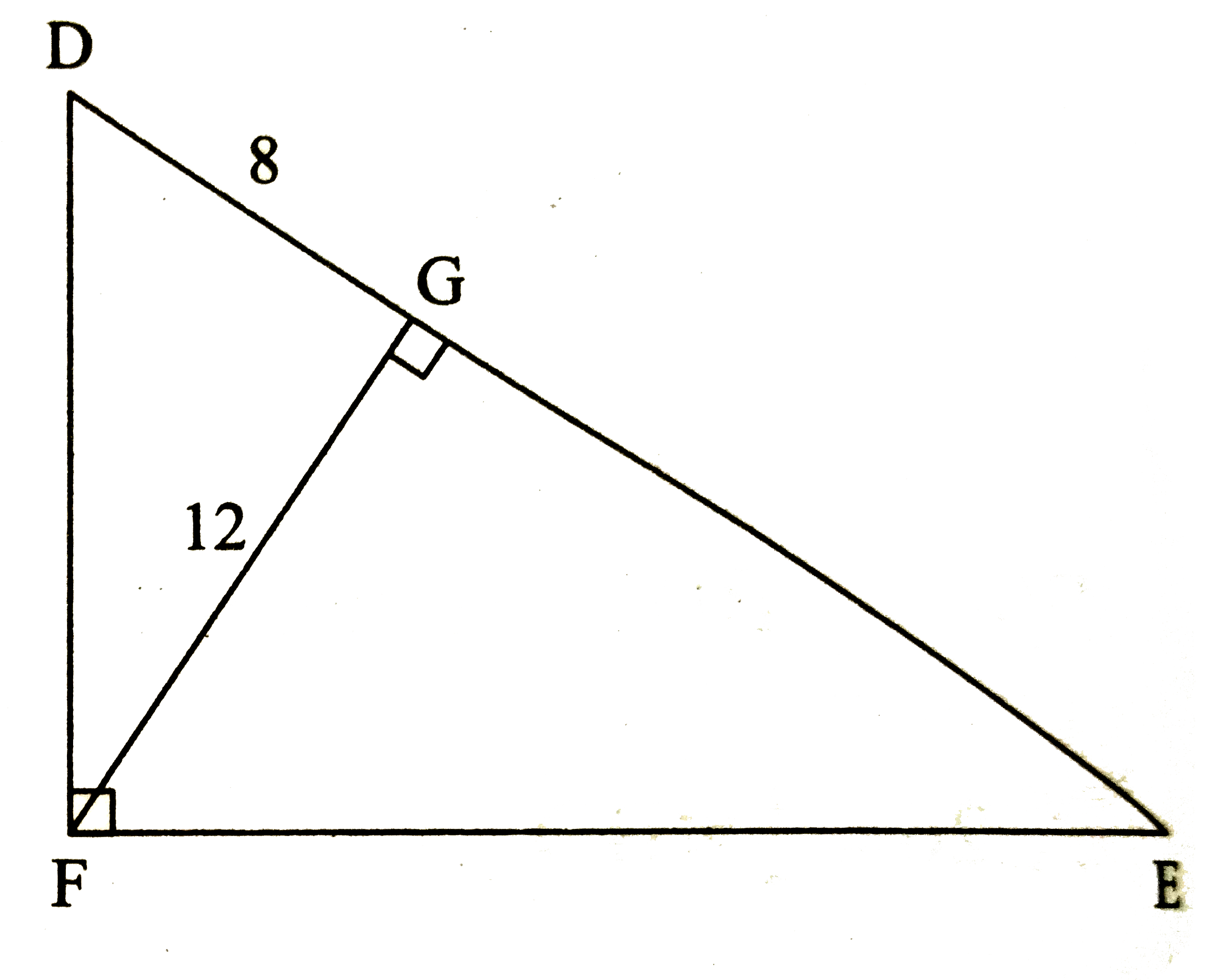
In ΔDFE, ∠DFE=90∘,
seg FG⊥ hypotenuse DE
∴ by theorem of geometric mean,
FG2=□×EG
∴122=□×EG
EG=12×12□
∴EG=□
DE=DG+GE=8+□=□
View SolutionIf sides of a square is (x+2y-z) units then the area of the square is.......
View Solution