In ΔABC seg MN∣∣ side AC. Seg MN divides ΔABC into two parts equal in area. Determine MBAB.
Video Solution
Text Solution
The correct Answer is:MBAB=√2−1√2
NA
|
Similar Questions
Knowledge Check
In ΔABC, D and E are points on AB and AC respectively such that DE||BC and DE divides the ΔABC into two parts of equal areas. Then ratio of AD and BD is
A1:1B1:√2−1C1:√2D1:√2+1In Figure the line segment XY is parallel to side AC of ΔABCand it divides the triangle into two parts of equal areas. Find the ratio AXAB.
A√2+1+√2B2−√2:2C1:√2D1:1In ΔABC, XY is parallel to BC and it divides the triangle into two equal areas (X lies on AB and Y lies on AC) then BX:AB equals
A√2:√2−1B1:1C2:1D√2−1:√2
In Figure the line segment XY is parallel to side AC of ΔABCand it divides the triangle into two parts of equal areas. Find the ratio AXAB.
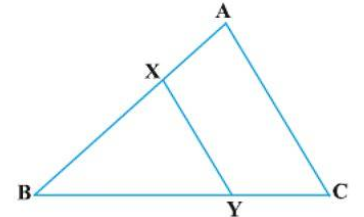
View SolutionIn ΔABC, PQ is a line segment which intersect AB on P and AC on Q so that PQ||BC and divides ΔABC in 2 equal parts of same area then find BPAB.
View SolutionIn ΔABC,AB=BC=k,AC=√2k, then ΔABC is a:
View SolutionIn ΔABC if AB is the greatest side then
View SolutionIn a ΔABC,AB=ACandAD⊥BC, then:
View Solution