AOB is a diameter of a circle with centre O and C is any point on the circle, joining A, C, B, C, and O, C, prove that
sin2∠BCO+sin2∠ACO=1Solution in Bengali
since AOB is a diameter and C is any point on the circle,
∴∠ACB is a semicircular angle.
∴∠ACB=90∘
∴ AB is a hypotenuse of the right-angled triangle ABC.
Again, since ∠ACB=90∘,∴∠BAC+∠CBA=90∘.
sin2∠BCO+sin2∠ACO.
=sin2∠BCO+sin2∠OAC [∵OC=OA.∴∠ACO=∠OAC]
=sin2∠BCO+sin2∠CAB
=sin2∠BCO+sin2(90∘−∠ABC)
sin2∠BCO+cos2∠ABC
=sin2∠BCO+cos2∠OBC
=sin2∠BCO+cos2∠BCO [OB=OC,∴∠OBC=∠BCO]=1
Hence sin2∠BCO+sin2∠ACO=1
Similar Questions
In the Figure, OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA=2OD.
View SolutionIf two chords AB and AC of a circle with centre O are such that the centre O lies on the bisector of ∠BAC, prove that AB=AC , i.e. the chords are equal.
View SolutionIn Figure, ˆAB≅ˆAC and O is the centre of the circle. Prove that OA is the perpendicular bisector of BC
View SolutionIn Figure, AB=CB and O is the centre of the circle. Prove that BO bisects ∠ABC.
View SolutionIn any triangle ABC, prove that: sin(B−C)sin(B+C)=b2−c2a2
View SolutionDraw a circle with centre O and any radius. Draw AC and BD two perpendicular diameters of the circle. Join AB, BC, CD and DA .
View SolutionIn the circle with centre O and A,B,C are the points on the circle, ∠AOB=60∘. Find ∠ACB
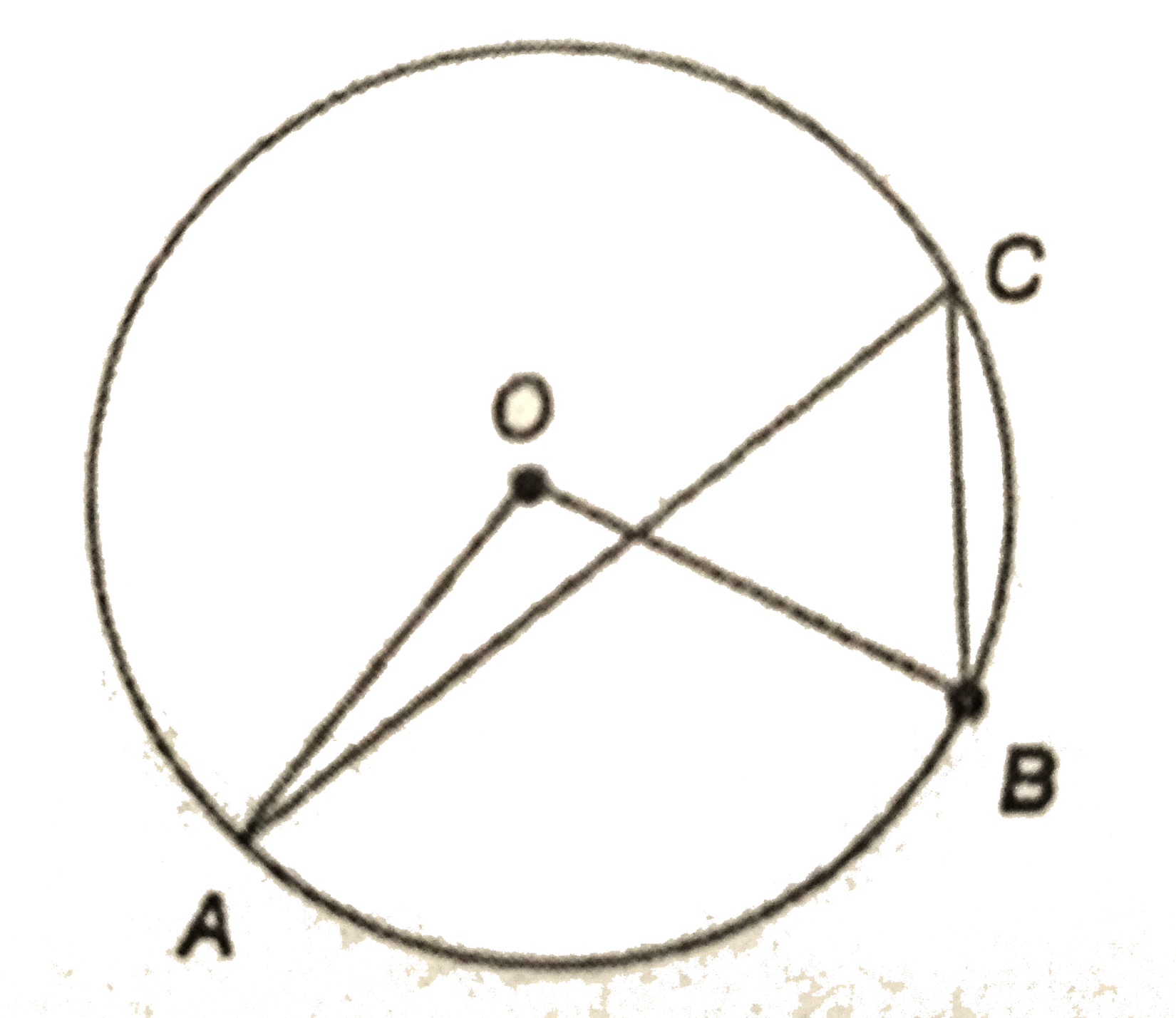
View SolutionAOB is diameter of a circle whose centre is O and C is any point on the circle. Join A and C , B and C and O and C. Show that (sin2∠BCO+sin2∠ACO)=1.
View Solution