Two particles A and B are thown vertically upward with velocity, vertically upward with velocity, 5ms−1 and 10ms−1 respectively (g=10 m s^(-2)), Find separation between them after 1s.
 .
.
Method -1: Position of A aftre 1 s
SaA=ut−12gt2
=5t−12×10×t2=5×1−5×12=5−5=0
i.e., the particle will return to ground at t=1s
SB=ut−12gt2=10×1−12×10×12=10−5=5m
Hence, separation between A and B, SB−SA=5m
Method-2: Relative velocity method:
→aBA=→vA=10−5=5ms−1
Hence, relative separation between particles
becuase→sBA(∈1s)=→vBA×t=5×1=5m
becuase Distance between A and B after 1s=5m.
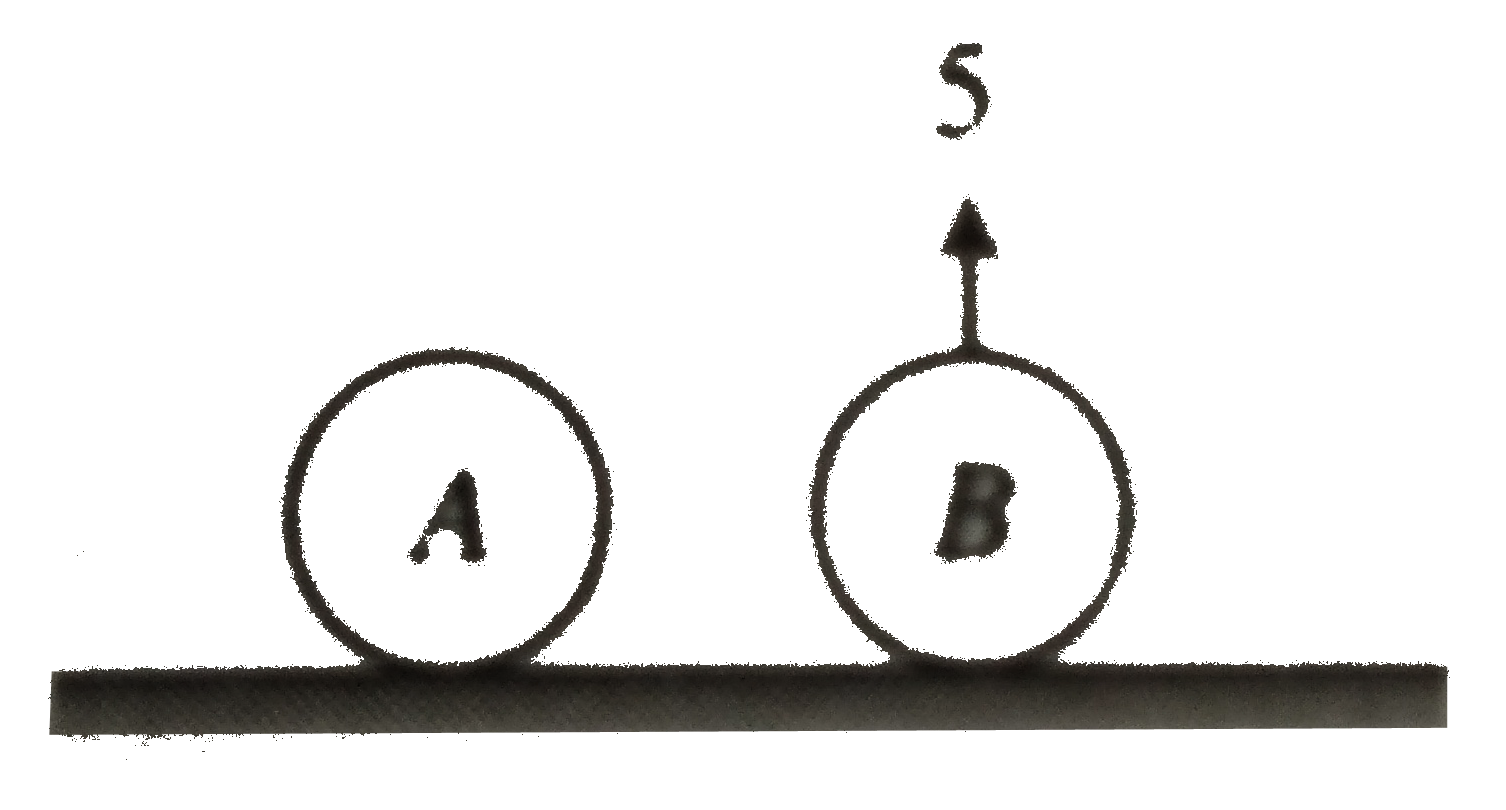 .
.
Similar Questions
Knowledge Check
If a ball is thrown vertically upwards with a velocity of 40m/s, then velocity of the ball after 2s will be (g=10m/s2)
A15m/sB20m/sC25m/sD28m/sFind the maximum height reached by a particle which is thrown vertically upwards with the velocity of 20m/s (take g=10m/s2).
A40 mB10 mC20 mDzeroA ball is thrown vertically upward with a velocity of 20 m/s . After 3s , the magnitude of its displacement is (take g = 10 m/s2)
A15 mB25 mC10 mD20 m
A particle is thrown vertically upward. Its velocity at half of the height is 10 m/s. Then the maximum height attained by it : -
(g=10m/s2)
View SolutionTwo particles projected vertically upward from points (0,0) and (1,0)m with uniform velocity 10m/s and vm/s respectively, as shown in the figure. It is found that they collide after time t in space. Time t is 15(√x−1). Calculate x
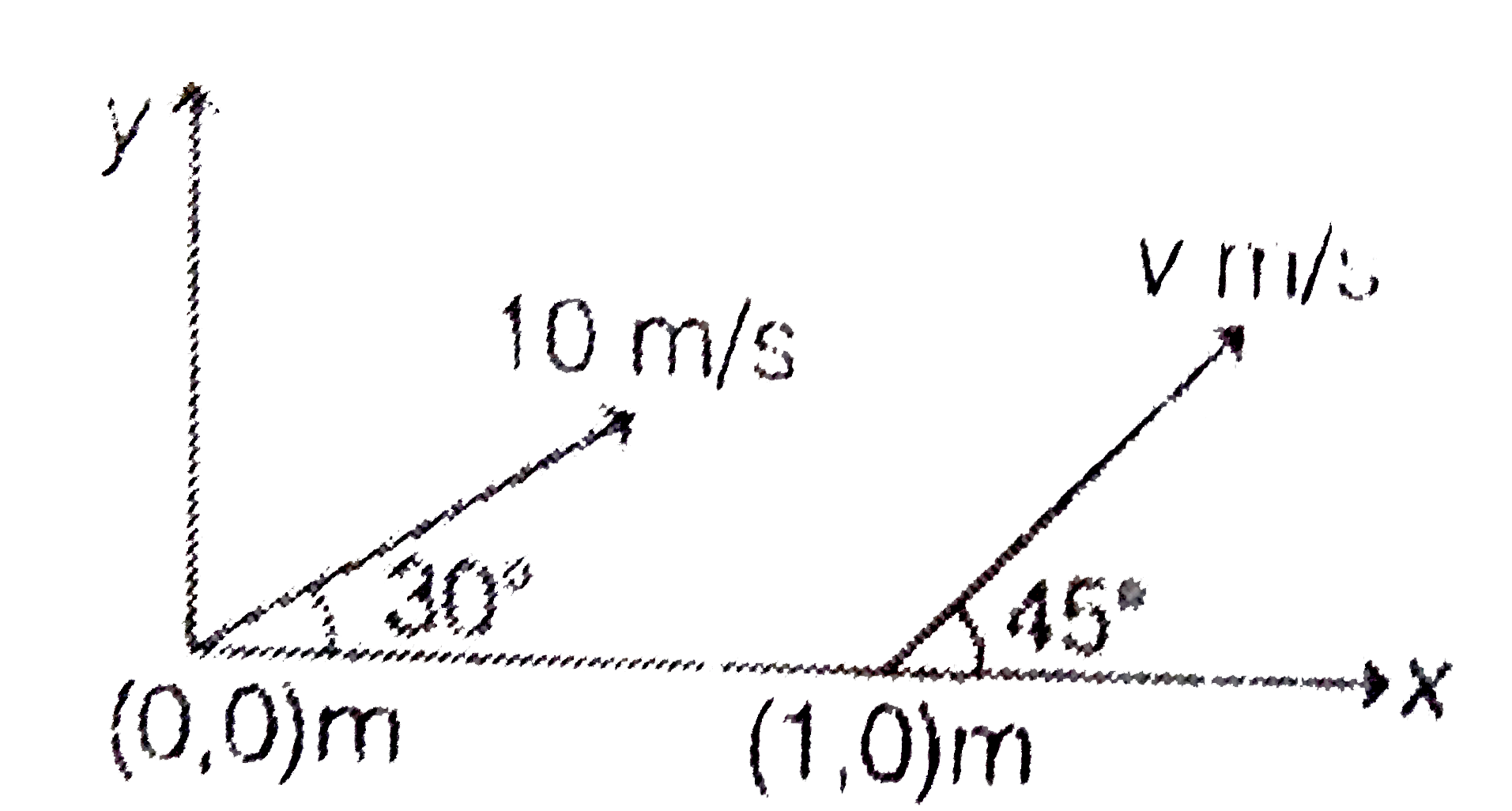
View SolutionA ball thrown vertically upwards with an initial velocity of 1.4m/s. The total displcement of the ball is
View SolutionTwo particles A and B are projected simultaneously in the direction shown in the figure with velocities VA=20m/s and VB=10m/s respectively. If they collide in air after 1/2 sec. then

View SolutionA stone of 200g is thrown vertically upward at a velocity of 60m/s. The kientic energy of the stone after 7s will be (g=10m/s2)
View Solution
