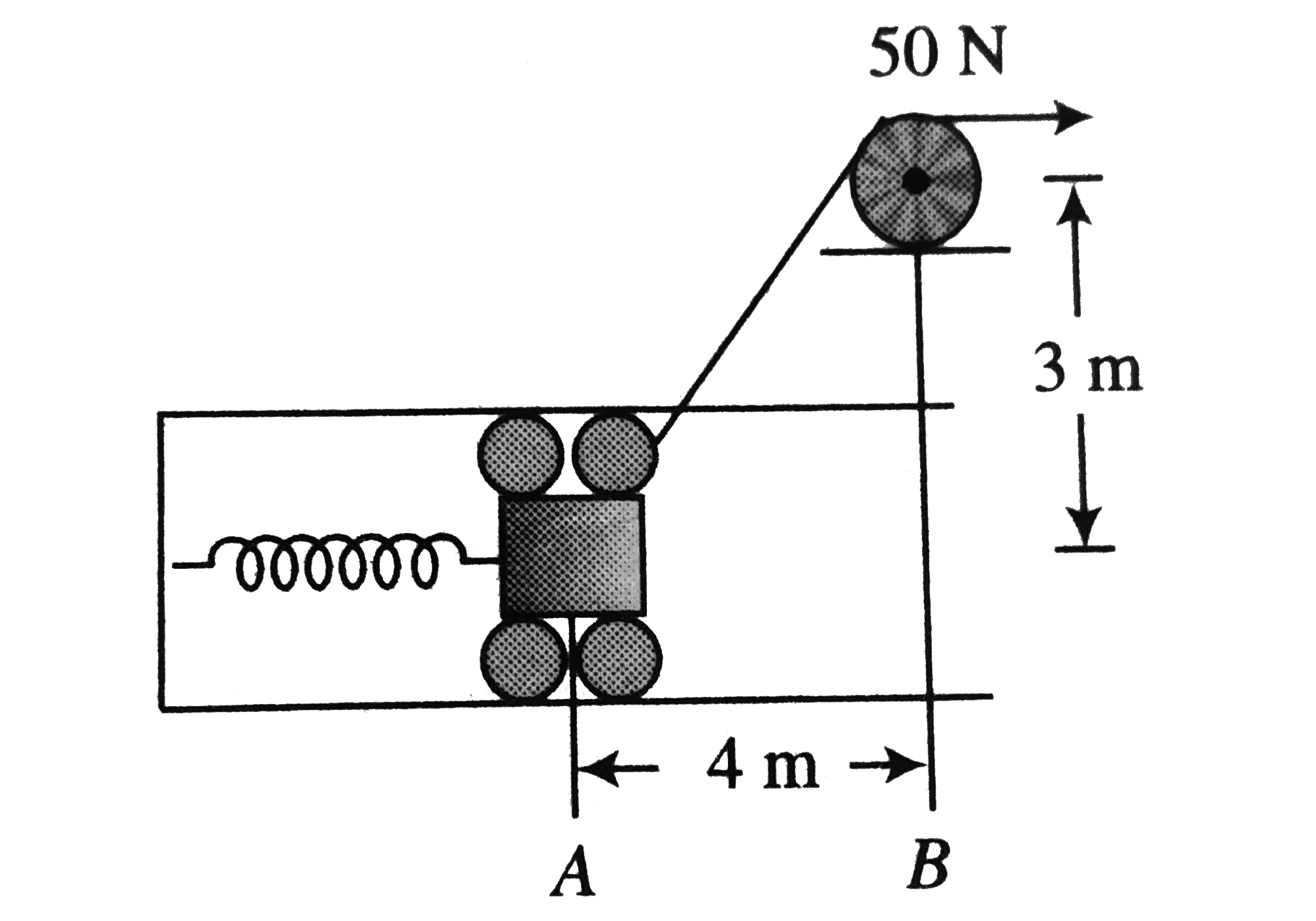
A 20−kg block attached to a spring of spring constant 5Nm−1 is released from rest at A. The spring at this instant is having an elongation of 1m. The block is allowed to move in smooth horizontal slot with the help of a constant force 50N in the rope as shown. The velocity of the block as it reaches B is (assume the rope to be light)
(a) 4ms−1
(b) 2ms−1
(c) 1ms−1
(d) 3ms−1
The correct Answer is:B
Consider the rope and the block as a system. From work-energy theorem, ΔK=Wnet
Here only two forces do not-zero work on the system: one is the spring force and the other is the constant force of 50N acting on the cable. Let v be the speed of the block when it reaches B, then
mv22−0=−[k×522−k×122]+work done by 50N force.
Horizontal displacement of the rope over pulley as the block moves from A to B is x=√42+32−3=2m, this is same as displacement of point of application of 50N force.
So, mv22=−[5×522−5×122]+50×2
=20×v22=40⇒v=2ms−1
Similar Questions
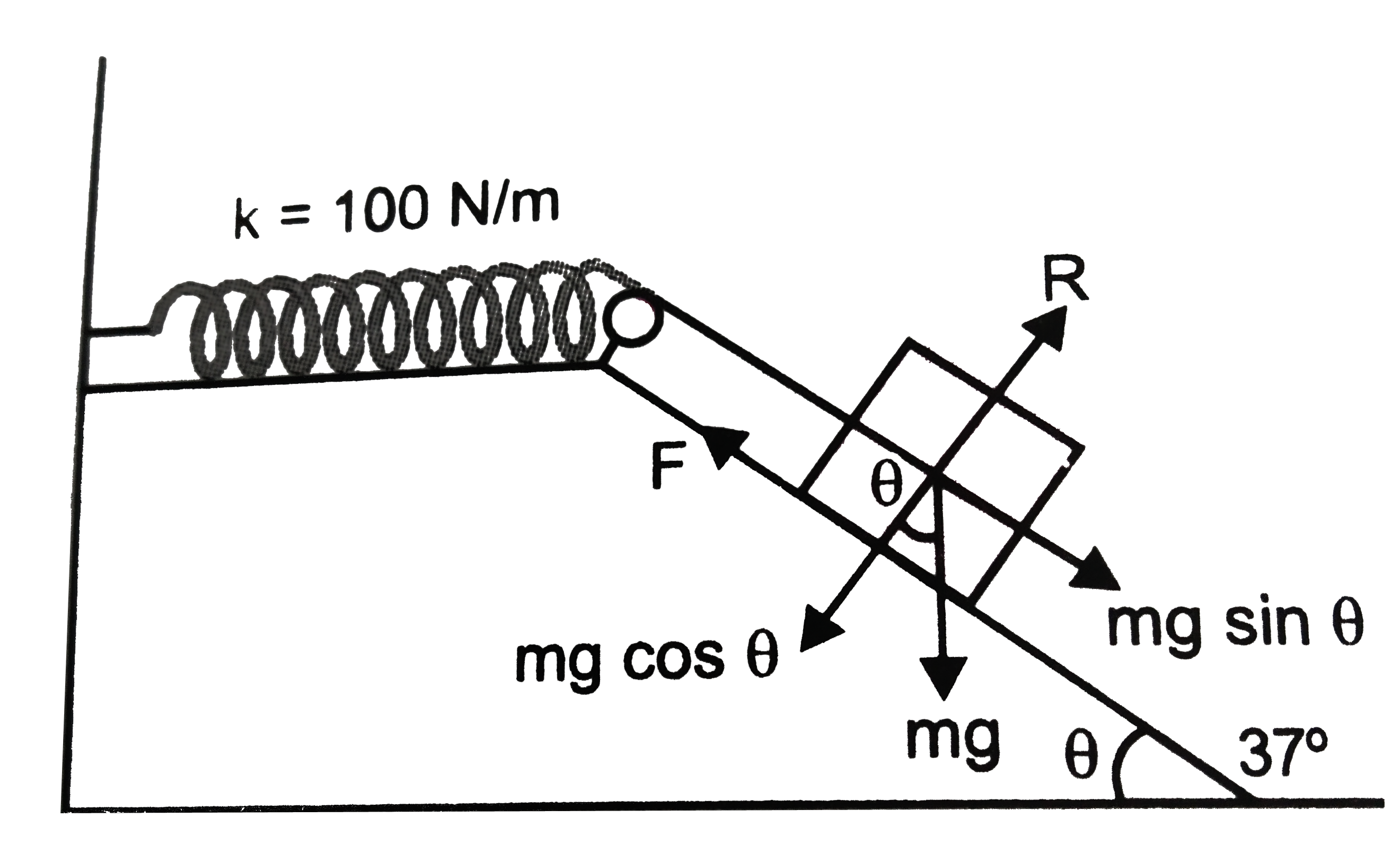
A 1kg block situated on a rough incline is connected to a spring of spring constant 100Nm−1 as shown in figure,. The block is released from rest with the spring in the unstretched position. The block moves 10cm down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has negligible mass and the pulley is frictionless.
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View Solution
Knowledge Check
A block is dragged on a smooth plane with the help of a rope which moves with a velocity v as shown in figure. The horizontal velocity of the block is :
 AvBvsinθCvsinθDvcosθ
AvBvsinθCvsinθDvcosθA 10 kg metal block is attached to a spring constant 1000Nm−1. A block is displaced from equilibrium position by 10 cm and released. The maximum acceleration of the block is
A10ms−2B100ms−2C200ms−2D0.1ms−2A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A block of mass 0.1 kg attached to a spring of spring constant 400 N/m is pulled rightward from x0=0 to x1=15 mm. Find the work done by spring force.
View SolutionA rope of mass 0.5kg is pulling a block of mass 10kg under the action of force of 31.5N If the block is resting on a smooth horizontal surface calculate the force of reaction exerted by the block on the rope .
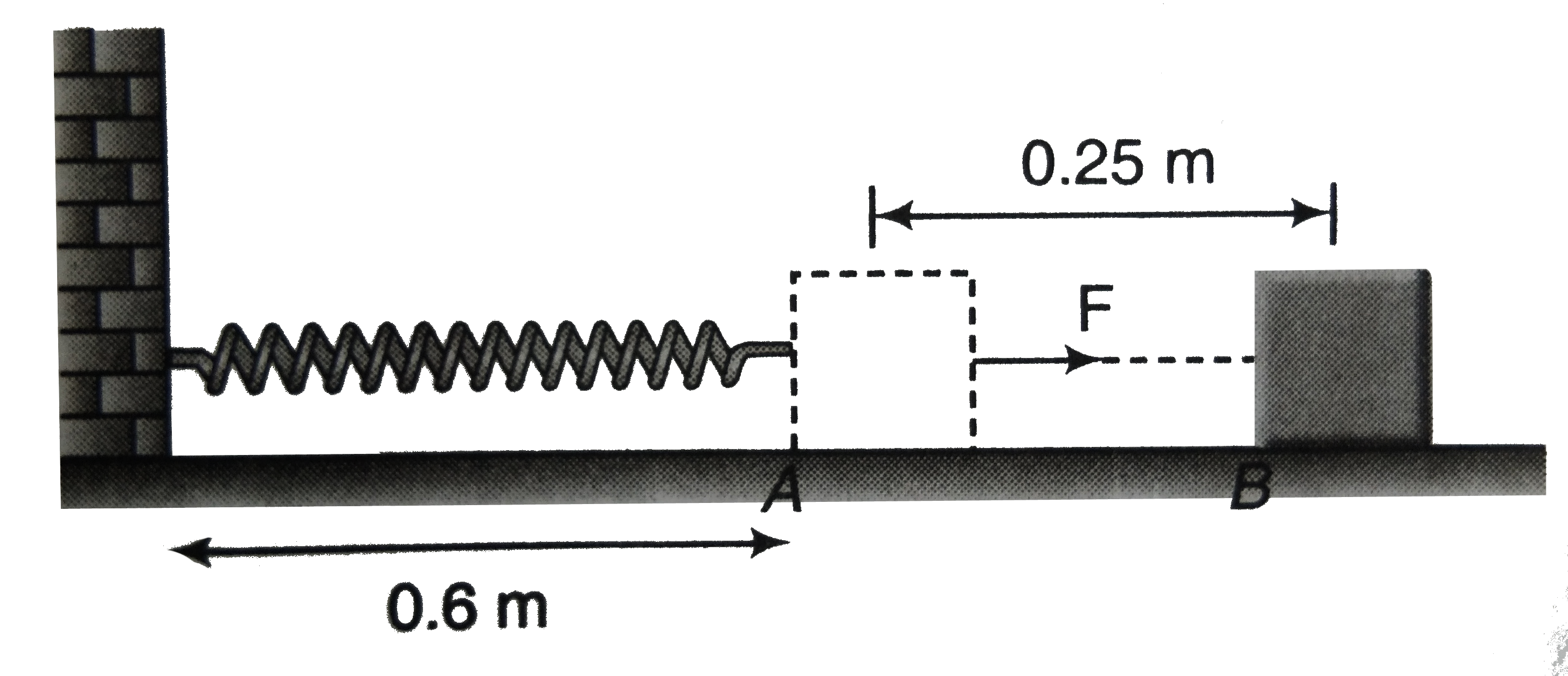
View SolutionA 0.500kg block is attached to a spring with length 0.60m and force constant k=40.0N/m. The mass of the spring is negligible. You pull the block to the right along the surgace with a constant horizontal force F=20.0N. (a) What is the block's speed when the block reaches point B,which is 0.25m to the right of right of point A? (b) What the block reaches point B, you let go off the block. In the subsequent motion, how close dies the block get to the wall where the lift end of the spring is attached? Neglect size of block and friction.
 .
.
View SolutionA block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.

View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10N/m.
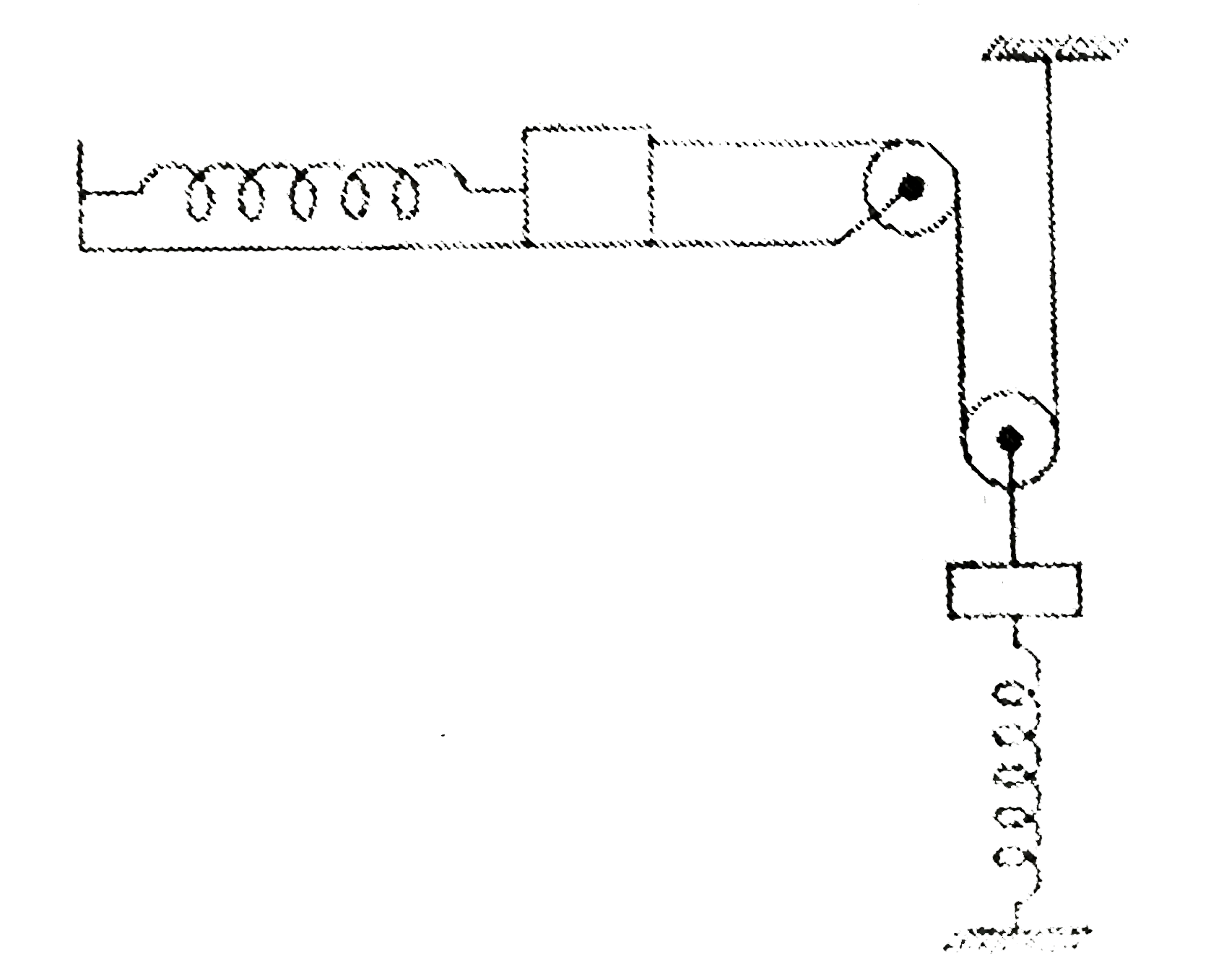
Extension of horizontal spring in equilibrium is
View Solution
