Two pulses having equal and opposite displacements
moving in oppositee directions overlap at t=t1 sec.
The resultant displacement of the wave at t=t1 sec is
twice the displacement of each pulse
half the displacement of each pulse
zero
Either (a) or (c )
The correct Answer is:c
To solve the problem of two pulses having equal and opposite displacements moving in opposite directions, we can follow these steps:
1. Understand the Pulses: We have two pulses that are equal in amplitude but have opposite displacements. Let's denote the amplitude of the first pulse as A (moving in the positive direction) and the second pulse as −A (moving in the negative direction).
2. Identify the Time of Overlap: The pulses overlap at t=t1 seconds. At this moment, we need to find the resultant displacement of the wave.
3. Apply the Principle of Superposition: According to the principle of superposition, when two waves overlap, the resultant displacement is the algebraic sum of the individual displacements.
yresultant=y1+y2
Here, y1=A (displacement of the first pulse) and y2=−A (displacement of the second pulse).
4. Calculate the Resultant Displacement: Substitute the values of y1 and y2 into the equation:
yresultant=A+(−A)=A−A=0
5. Conclusion: The resultant displacement of the wave at t=t1 seconds is 0.
Final Answer:
The resultant displacement of the wave at t=t1 seconds is 0.
---
The resultant displacement of the wave at t=t1 seconds is 0.
Similar Questions
Knowledge Check
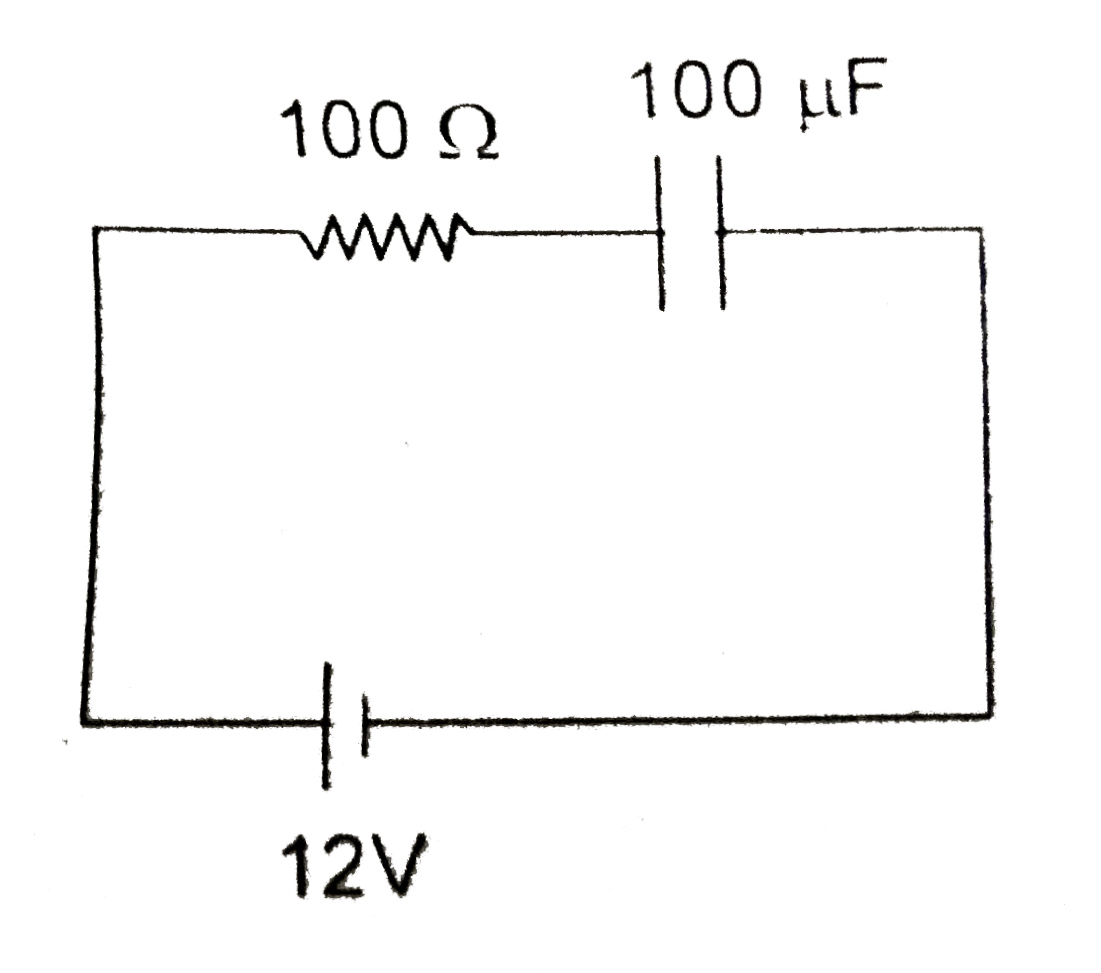
The value of displacement current at t=1 time constant isA120eB120e2C120 mADnone of theseThe relation 3t=√3x+6 describe the displacement of a particle in one direction where x is in metres and t in sec.
The displacement, when velocity is zero isA24 metresB12 metresC5 metresDzeroIn the above question, the displacement of particle at t = 1 sec and x = 4 cm is:
A4 cmB2cmC1cmDZero
The angular displacement of a particle is given by θ=t3+t2+t+1 then,the angular acceleration of the particle at t=2 sec is …….rad s^(-2)
View SolutionThe displacement is given by x=2t2+t+5 , the acceleration at t = 5 sec will be-
View SolutionIf the displacement of a particle is given by s=2t3−5t2+4t−3, then its displacement when acceleration is 14 ft/sec2, is
View SolutionA particle moves along a straight line such that its displacement at any time t is given by s=3t3+7t2+14t+5. The acceleration of the particle at t=1s is
View SolutionThe displacement of a particle in time t is given by s=2t2−3t+1. The acceleration is
View Solution
