Two blocks A and B of masses m and 2m, respectively are connected by a spring of force constant k. The masses are moving to the right with uniform velocity v each, the heavier mass leading the lighter one. The spring is in the natural length during this motion. Block B collides head on with a third block C of mass m, at rest, the collision being completely inelastic. Calculate the maximum compression of the spring.
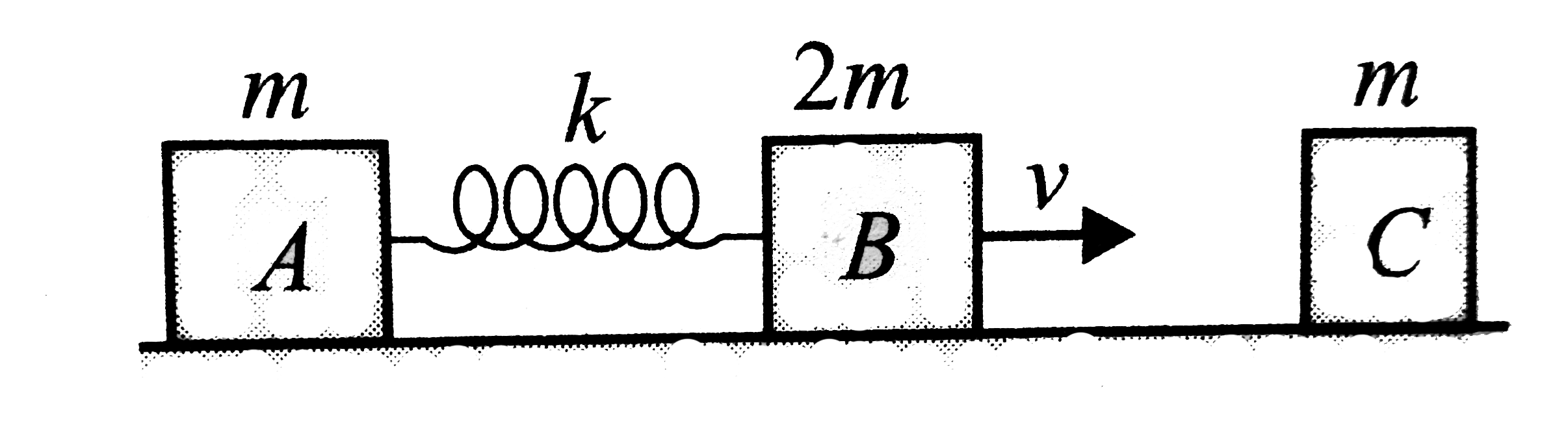
The correct Answer is:x=√mv212k
First considering an inelastic collision between B and C.
2mv(m+2m)vB
vB=23v velocity of (B and C)
Then velocity of centre of mass during maximum compression
vCM=3mv4m=34v

12mv24+123mv2(b+c)=124mv2CM+12kx2
Then substituting the value x=√mv212k
Similar Questions
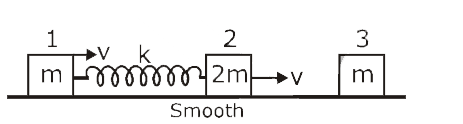
Two blocks 1 and 2 of masses m and 2m respectively are connected by a spring of force constant k. The masses are moving to the right with uniform velocity v each, the heavier mass, leading the lighter one. The spring is of natural length in the motion. Block 2 collides head on with a third block 3 of mass m, at rest, the collision being completely inelastic. Determine the velocity of blocks at the instant of maximum compression of the spring.
View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View Solution
Knowledge Check
Two block A and B of masses m and 2m respectively are connected by a spring of spring cosntant k. The masses are moving to the right with a uniform velocity v0 each, the heavier mass leading the lighter one. The spring is of natural length during this motion. Block B collides head on with a thrid block C of mass 2m. at rest, the collision being completely inelastic.
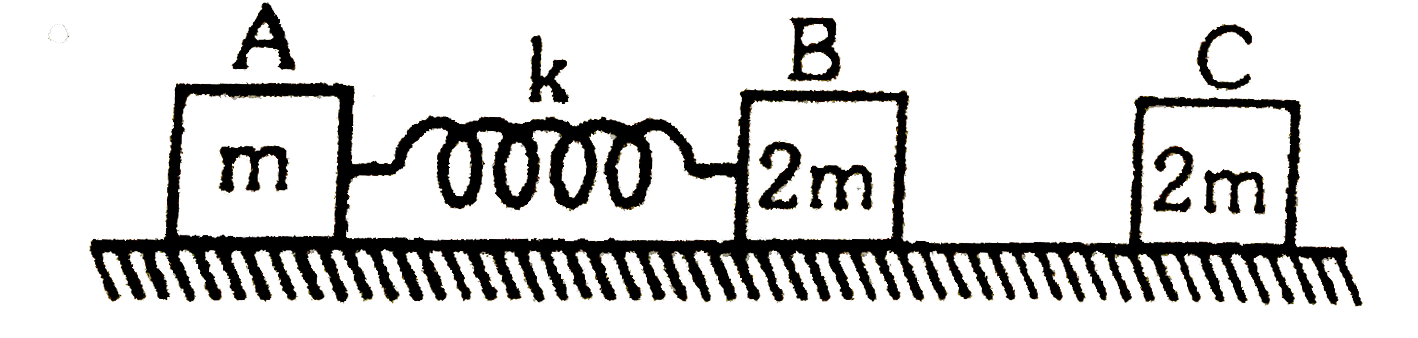
The maximum compression of the spring after collision is -A√mv2012kB√mv205kC√mv2010kDNone of theseTwo block A and B of masses m and 2m respectively are connected by a spring of spring cosntant k. The masses are moving to the right with a uniform velocity v0 each, the heavier mass leading the lighter one. The spring is of natural length during this motion. Block B collides head on with a thrid block C of mass 2m. at rest, the collision being completely inelastic.

The velocity of block B just after collision is -Av0Bv02C3v05D2v05Two block A and B of masses m and 2m respectively are connected by a spring of spring cosntant k. The masses are moving to the right with a uniform velocity v0 each, the heavier mass leading the lighter one. The spring is of natural length during this motion. Block B collides head on with a thrid block C of mass 2m. at rest, the collision being completely inelastic.
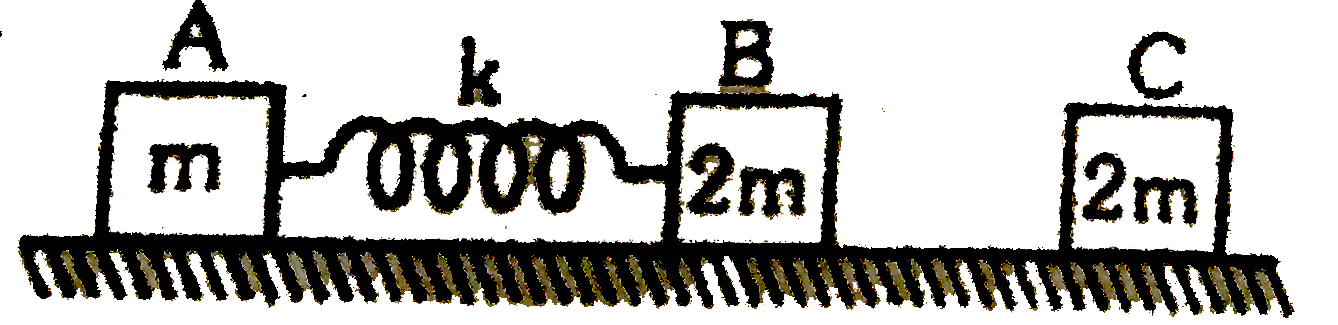
The velocity of centre of mass of system of block A, B, & C is -Av0B3v05C2v05Dv02
Two blocks A and B of masses m and 2m, respectively , are connected by a massless spring of force constant k and are placed on a smooth horizontal plane. The spring is stretched by an amount x and then released . The relative velocity of the blocks when the spring comes to its natural length is

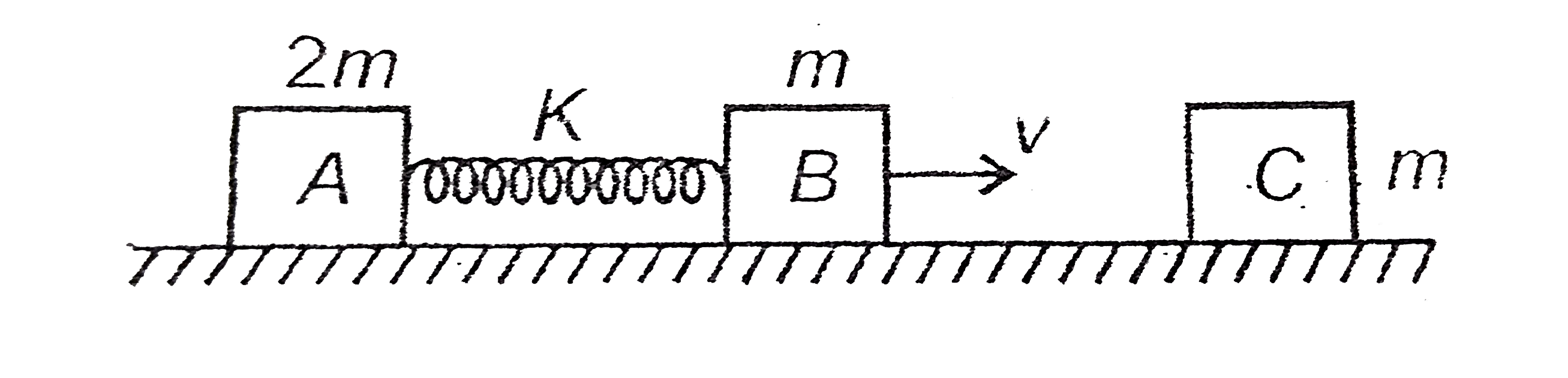
View SolutionTwo blocks A and B of mass 2m and m respectively are connected to a massless spring of force constant K as shown in figure A and B are moving on the horizontal frcitionless surface with velocity v to right with underformed spring. If B collides with C elastically, then maximum compression of the spring will be
View SolutionA ball of mass m moving with speed v0 strikes a block of mass 3m kept at rest. The collision is completely inelastic . If k is spring constant , the maximum compression of the spring is
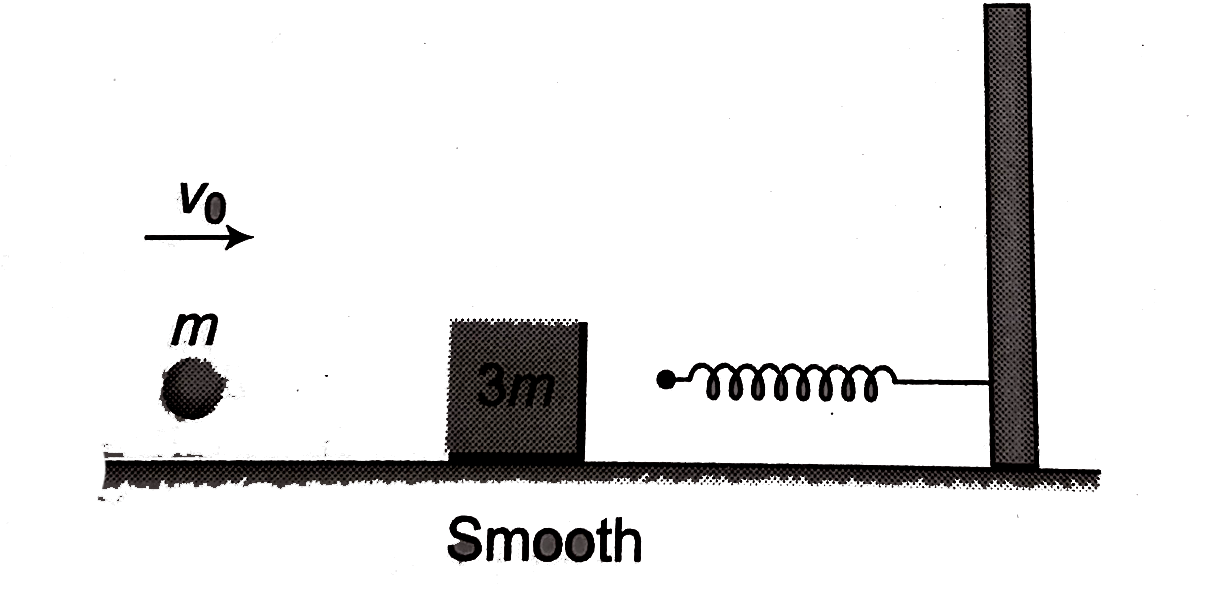
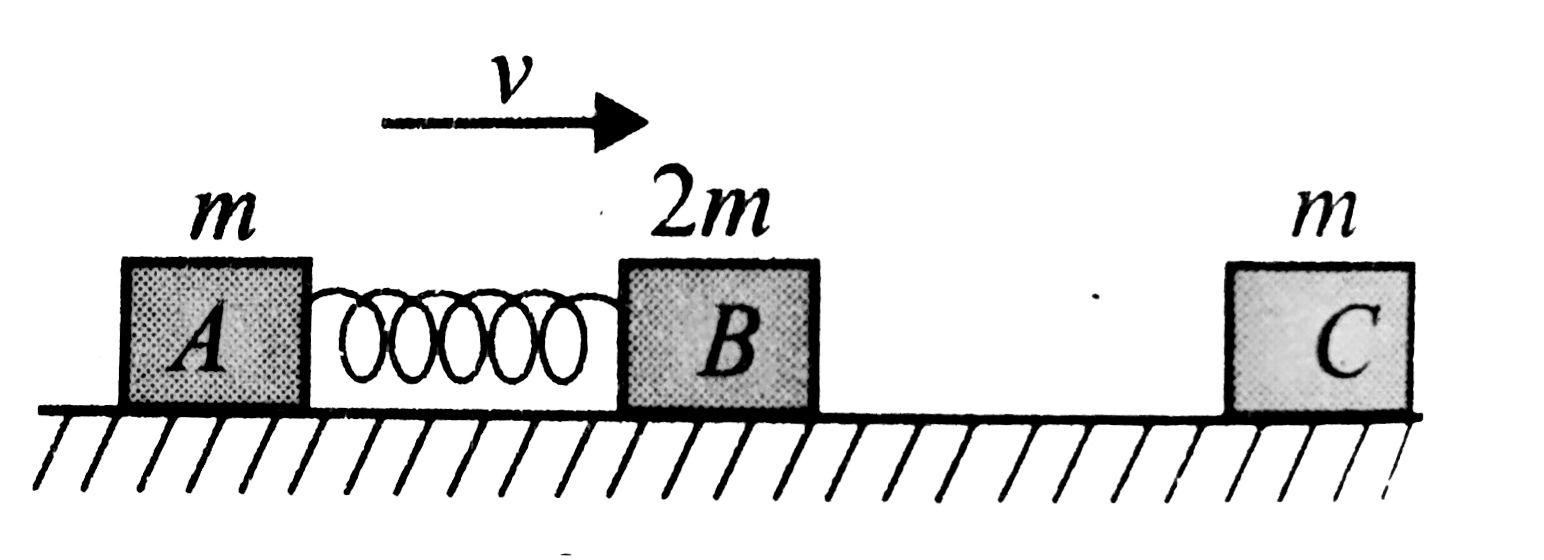
View SolutionTwo blocks A and B of masses in and 2m, respectively, are connected with the help of a spring having spring constant, k as shown in Fig. Initially, both the blocks arc moving with same velocity v on a smooth horizontal plane with the spring in its natural length. During their course of motion, block B makes an inelastic collision with block C of mass m which is initially at rest. The coefficient of restitution for the collision is 1/2. The maximum compression in the spring is
View Solution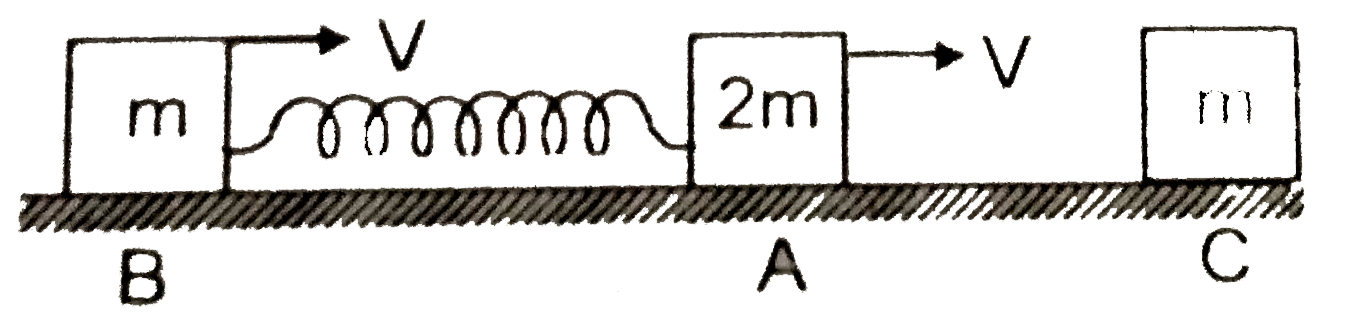
Two blocks A and B of mass 2 m and m respectively are connected to a massless spring of spring constant K. if A and B moving on the horizontal frictionless surface with velocity v to right. If A collides with C of mass m elastically and head on, then the maximum compressions of the spring will be
View Solution

