A horizontal frictionless rod is threaded through a bead of mass m. The length of the cart is L and the radius of the bead, r, is very small in comparison with L(r<<L). Initially at (t=0) the bead is at the right edge of the cart. The can is struck and as a result, it moves with velocity v0 towards right. When the bead collides with the cart's walls, the collisions are always completely elastic.
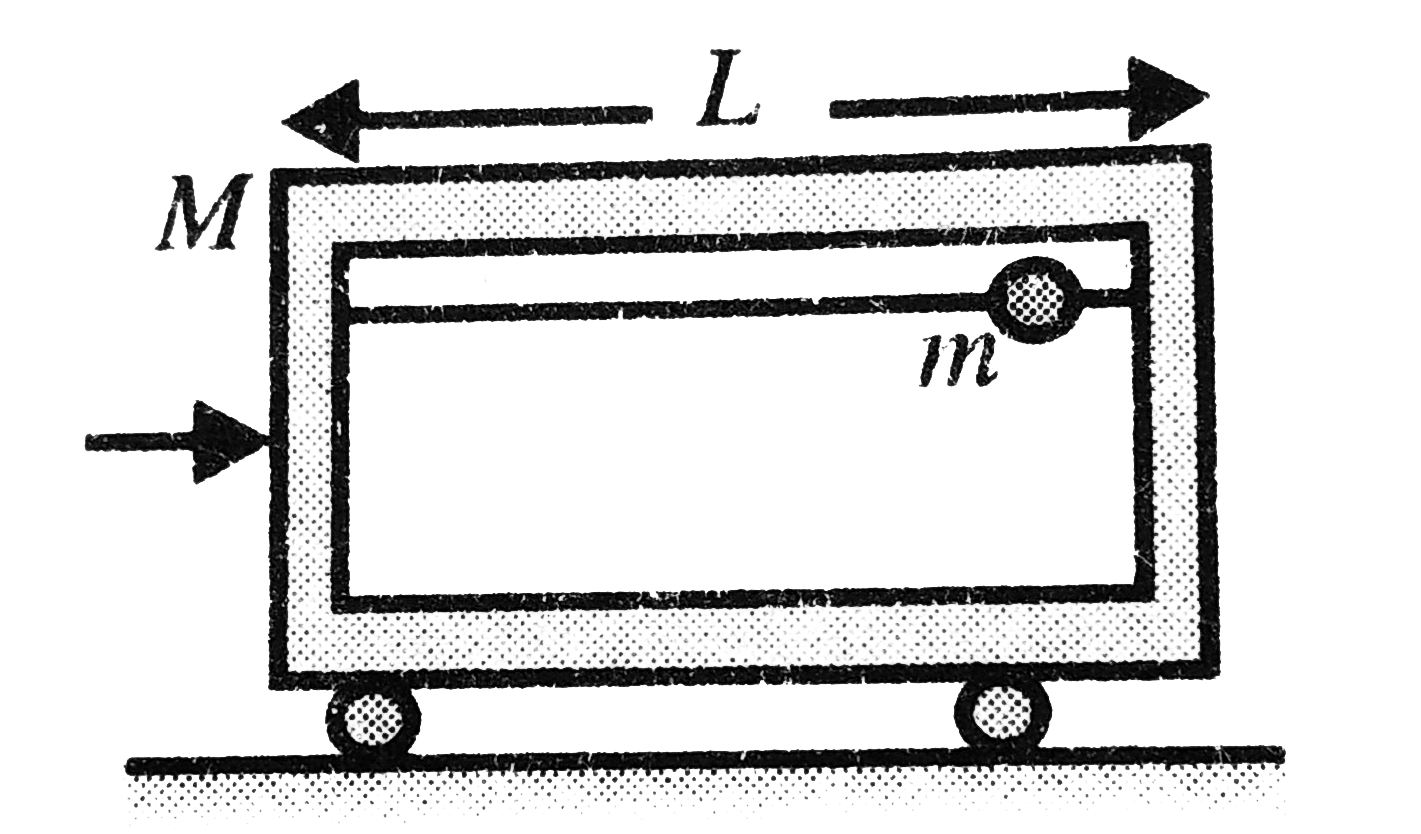
What is the velocity of the cart just after the first collision?
−mv0m+M
Mv0m+M
M−mM+mv0
2Mm+Mv0
The correct Answer is:C

Mv0=Mv1+mv2…………i
v2−v1v0=………..ii
Solve to get v1=M−mM+mv0
v2=2Mm+Mv0
Similar Questions
A thin insulating wire is stretched·along the diameter of an. insulated circular hoop of radius R. A small bead of mass m and charge-q is threaded onto the wire. Two small identical charges are tied to the hoop at points opposite to each other, so that the diameter passing through them is perpendicular to the thread as shown in figure. The bead is released at a point which.is located at a distance x0 from the centre of the hoop. Assume that x0<<R.
(a) What is the resultant force acting on the charged bead?
(b) Describe the motion of the bead after it is released X
(c) Use the assumption that xR<<1 to obtain an approximate equation of motion, and find the displacement and velocity of the bead as functions of time
(d) When will the velocity of the bead will bcome zero for the first time?

View SolutionA bead of mass 5 kg is free to slide on the horizontal rod AB. They are connected to two identical springs of natural length h ms. As shown. If initially bead was at O & M is vertically below L then, velocity of bead at point N will be :

View SolutionA bead of mass m moves on a rod without friction. Initially the bead is at the middle of the rod and the rod moves translationally in a vertical plane with an acceleration a0 in a direction forming angle θ with the horizontal as shown in the given figure. The acceleration of bead with respect to rod is
View SolutionA smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with an angular velocity ω0 about an axis perpendicular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......

View Solutionएक लम्बी क्षैतिज छड़ पर एक मोती पिरोया गया है, यह छड़ कि लम्बाई के अनुदिश फिसल सकता है और प्रारम्भ में यह छड़ के एक सिरे A से L दुरी पर है । छड़ को A के पारित नियत कोणीय त्वरण α से घुमाया जाता है । यदि छड़ एवं मोती के बीच घर्षण गुणांक μ है और गुरुत्व को नगण्य माना जाये तो कितने समय पश्चात मोती फिसलना प्रारम्भ कर देगा ?
View SolutionA horizontal frictionless rod is threaded through a bead of mass m . The length of the cart is L and the radius of the bead, r , is very small in comparison with L(r lt lt L) . Initially at ( t = 0 ) the bead is at the right edge of the cart. The can is struck and as a result, it moves with velocity v_(0) towards right. When the bead collides with the cart's walls, the collisions are always completely elastic. What is the velocity of the cart just after the first collision?
View SolutionA horizontal frictionless rod is threaded through a bead of mass m . The length of the cart is L and the radius of the bead, r , is very small in comparison with L(r lt lt L) . Initially at ( t = 0 ) the bead is at the right edge of the cart. The can is struck and as a result, it moves with velocity v_(0) towards right. When the bead collides with the cart's walls, the collisions are always completely elastic. Velocity of bead just after the first collision is
View SolutionA horizontal frictionless rod is threaded through a bead of mass m. The length of the cart is L and the radius of the bead, r, is very small in comparison with L(r<<L). Initially at (t=0) the bead is at the right edge of the cart. The can is struck and as a result, it moves with velocity v0 towards right. When the bead collides with the cart's walls, the collisions are always completely elastic.
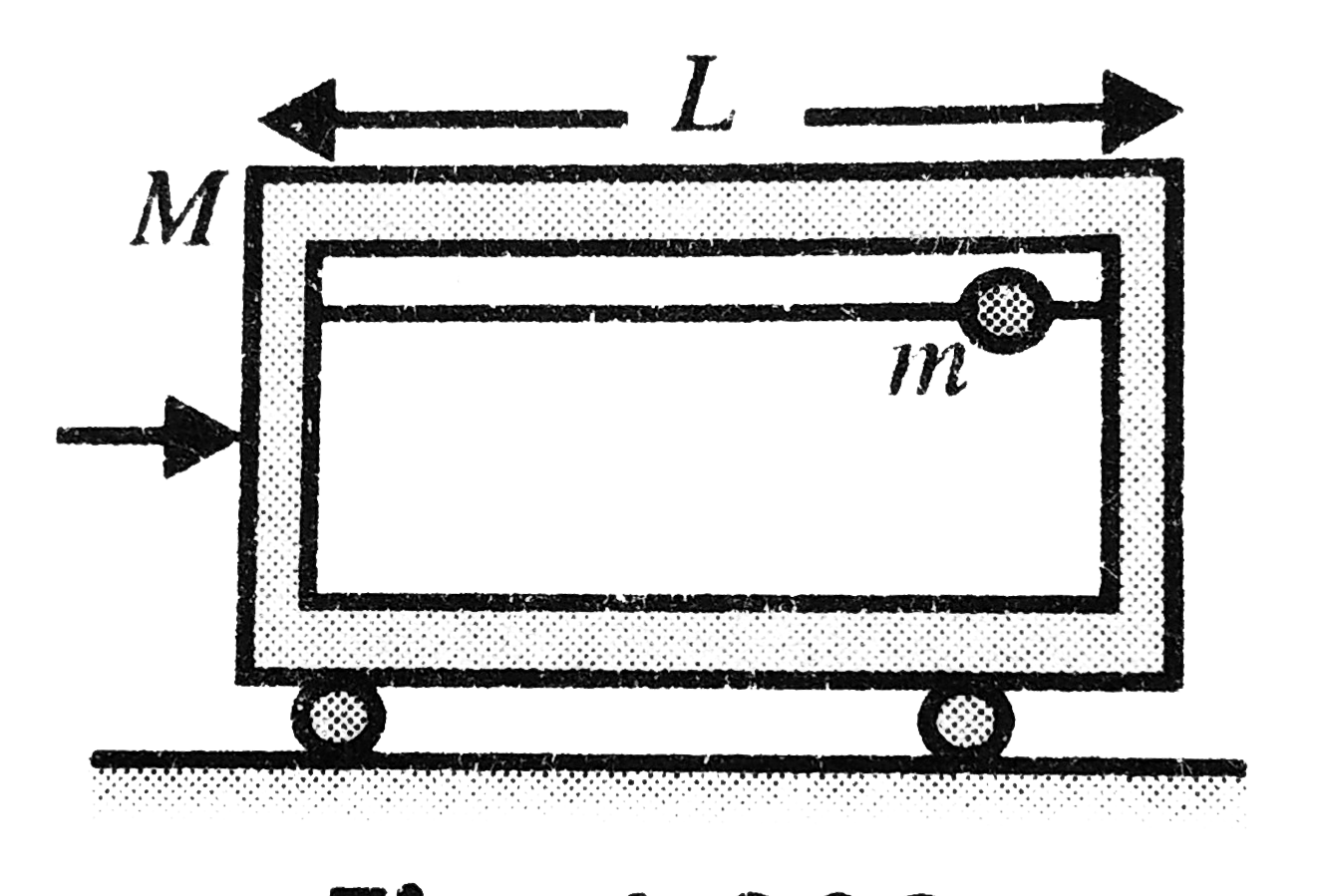
The first collision takes place at time ti and the second collision takes place at time t2. Find t2−t1
View Solution
