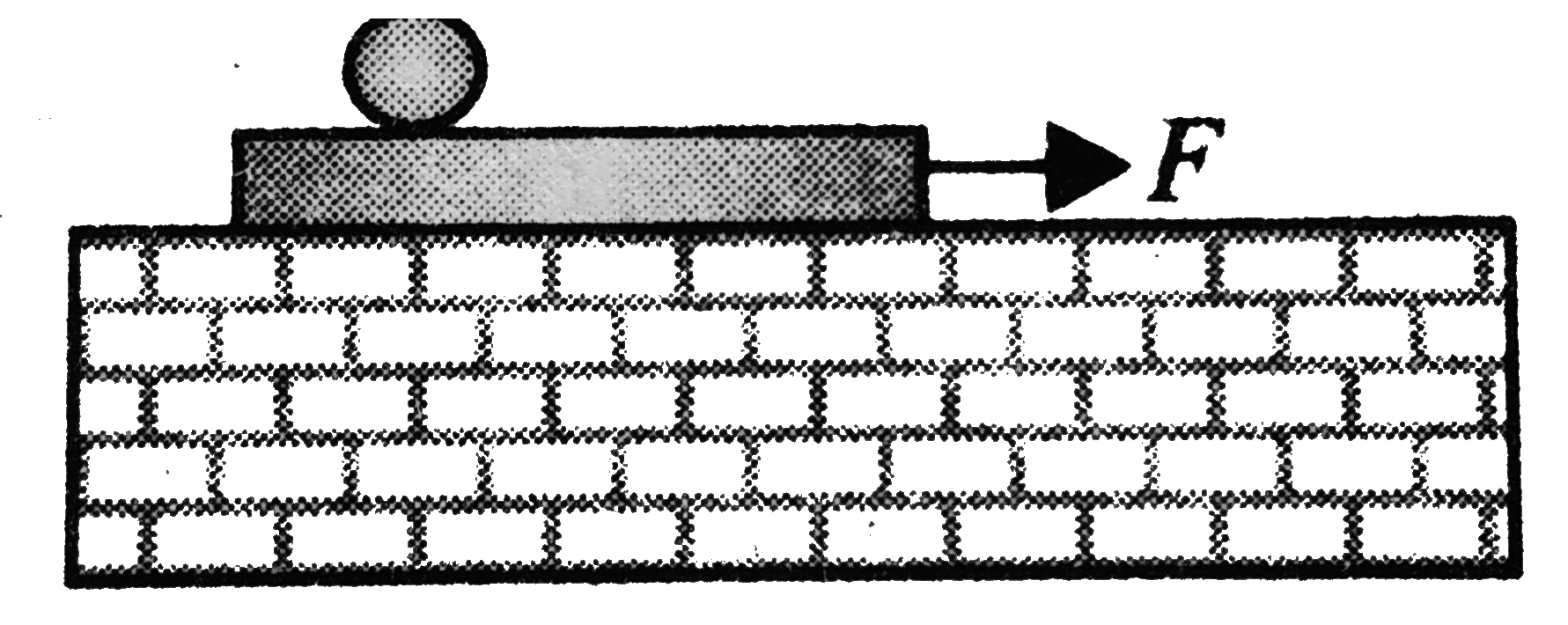
A plank of mass M, is placed on a smooth surface over which a cylinder of mas m(=M) annd radius R=1m is placed as shown in figure. Now the plane is pulled towards the right wilth an external force F(=2Mg). If the cyinder does not slip over the surfcace of the plank, find the linear acceleration of he plank and the cylinder and the angular acceleration of the cylinder. (Take g=10ms2)

Here we are give that cylinder does not sip over the plank surface, it is the case of pure rolling, we can se firction on cylinder in any direction. Here we choose towards the right. As friction is acting on the cylinder towards the right, it must be towards the left on the plank as shown in the force diagram of figure.
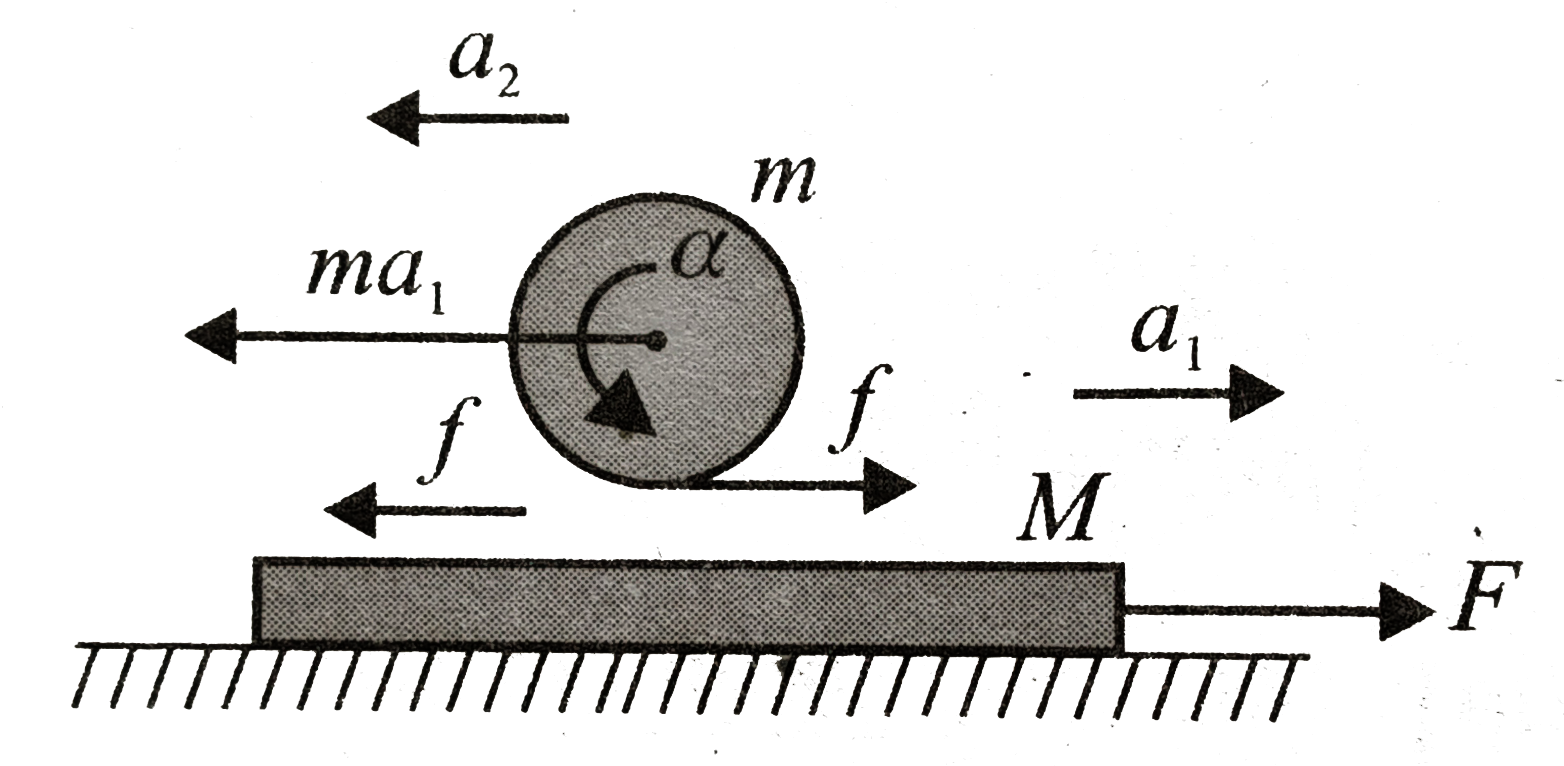
Let the plank move towards the right with an acceleration a1 the cylinder will experience a pseudoforce ma1 in the left direction, due to which it will roll towards the left with respect to the plank with an acceleration a2. As we have used pseudoforce, a2 must be with respect to the plank. Let it angular accelration during rolling be α, we have a2=Rα.
For tanslationa motion of the plank, we have
F−f=Ma1.............i
For translational motion of the cylinder with respect to the plank, we have
ma1−f=ma2 ........ii
For rotational motion of the cylinder with respect to the plank we have
fR=Iα
fR+(12mR2)(a2R)
or f=12ma2........iii
From eqn i and ii we get
ma1−12ma2=ma2
a1=32a2.........iv
Using eqn i, iii and iv we get
F−1q2ma2=32Ma2
a2=2F3M+m=10m/s2
From eqn iv a1=3F3M+m=15m/s2
As we have already discused that the value of a2 is relative to the plank, the net acceleration of the cylinder will be given as a1−a2.
Hence, the acceleration of the cylinder is
acylinder=a1−a2=15−10=5m/s2
The angular accelertionn of the cylinder is
α=a2R=10rad/s2
Similar Questions
A plank of mass M is placed on a smooth surface over which a cylinder of mass m and radius R is placed as shown in figure-5.63. Now the plank is pulled towards right with an external force F. If cylinder does not slip over the surface of plank find the linear acceleration of plank and cylinder and the angular acceleration of the cylinder.
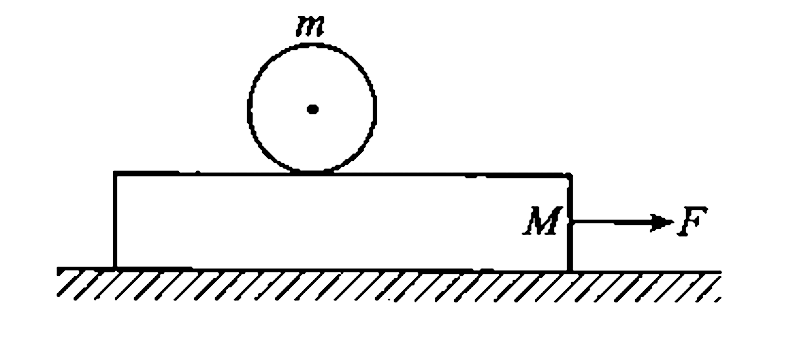
View SolutionA solid sphere of mass M and radius R is pulled by a force F as shown in figure . If the sphere does not slip over the surface , then frictional force acting on the sphere is

View Solution
Knowledge Check
In the figure shown, the plank is being pulled to the right with a constant speed v. If the cylinder does not slip then:
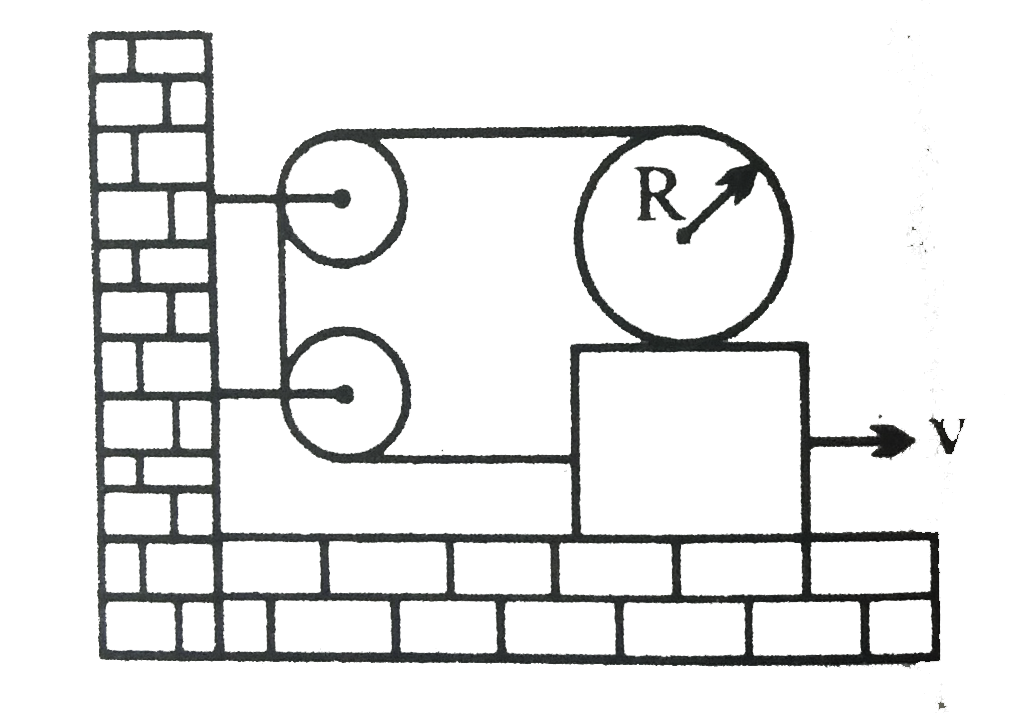 .Athe speed of the centre of mass of the cylinder is 2v.Bthe speed of the centre of mass of the cylinder is zero.Cthe angular velocity of the cylinder is v/R.Dthe angular velocity of the cylinder is zero.
.Athe speed of the centre of mass of the cylinder is 2v.Bthe speed of the centre of mass of the cylinder is zero.Cthe angular velocity of the cylinder is v/R.Dthe angular velocity of the cylinder is zero.A plank with a uniform sphere placed on it rests on a smooth horizontal plane. The plank is pulled to the right by a constant force F. It the sphere does not slip over the plank, then
 Aboth have the same accelerationBacceleration of the centre of sphere is less than that of the plankCwork done by friction acting on the sphere is equal to its total kinetic energyDtotal kinetic energy of the system is equal to work done by the force F
Aboth have the same accelerationBacceleration of the centre of sphere is less than that of the plankCwork done by friction acting on the sphere is equal to its total kinetic energyDtotal kinetic energy of the system is equal to work done by the force FA plank with a uniform sphere placed on it. Rests on a smooth horizontal plane. Plank is pulled to right by a constant force F. It the sphere does not slip over the plank.
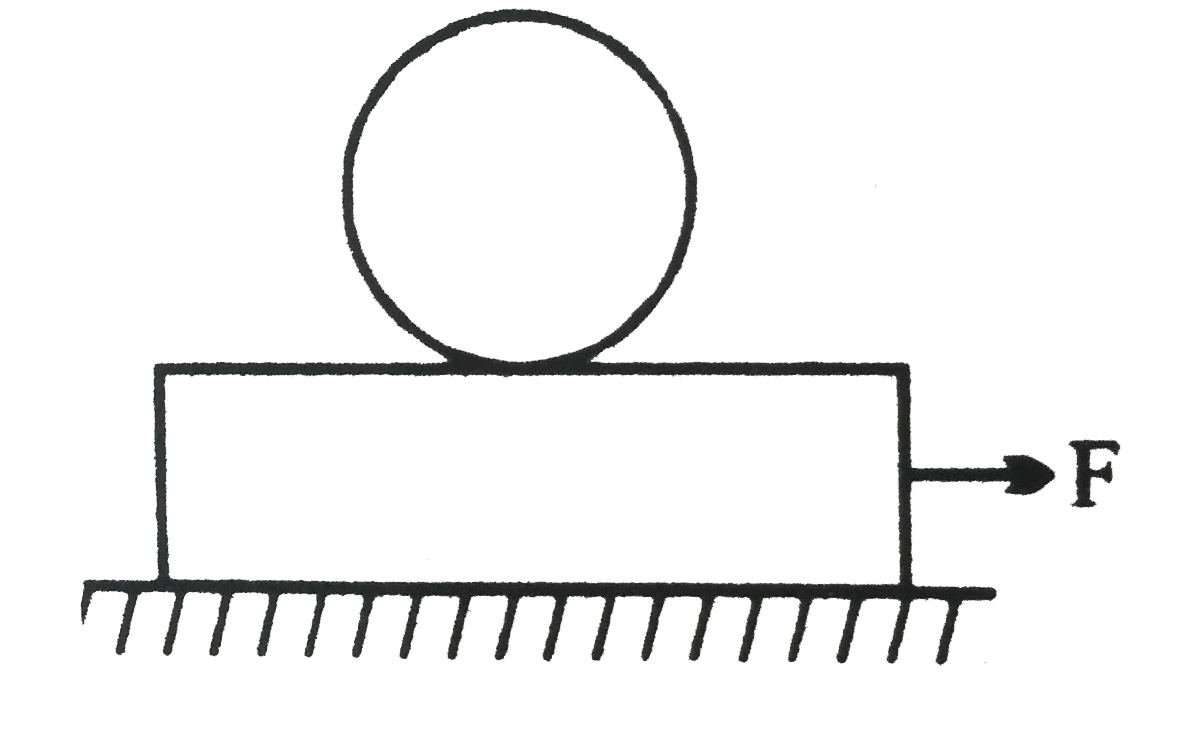 . Aacceleration of centre of sphere is less than that of the plankBacceleration of centre if sphere is grester than tha plank because friction acts rightward on the sphereCacceleration of the centre of sphere may be towards left.Dacceleration of the centre of sphere relative to plank may be greater than that of the plank relative to floor.
. Aacceleration of centre of sphere is less than that of the plankBacceleration of centre if sphere is grester than tha plank because friction acts rightward on the sphereCacceleration of the centre of sphere may be towards left.Dacceleration of the centre of sphere relative to plank may be greater than that of the plank relative to floor.
A sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionA plank of mass m is placed on a smooth surface. Now, a uniform solid sphere of equal mass m and radius R is placed on the plank as shown in the figure. A force F is applied at topmost point of the sphere at an angle of 45∘ to the horizontal. Surface between the plank and the sphere is extremely rough so that there is no slip between the plank and the sphere. The force of firction acting between the plank and the sphere is Fk√2. Find the value of k.
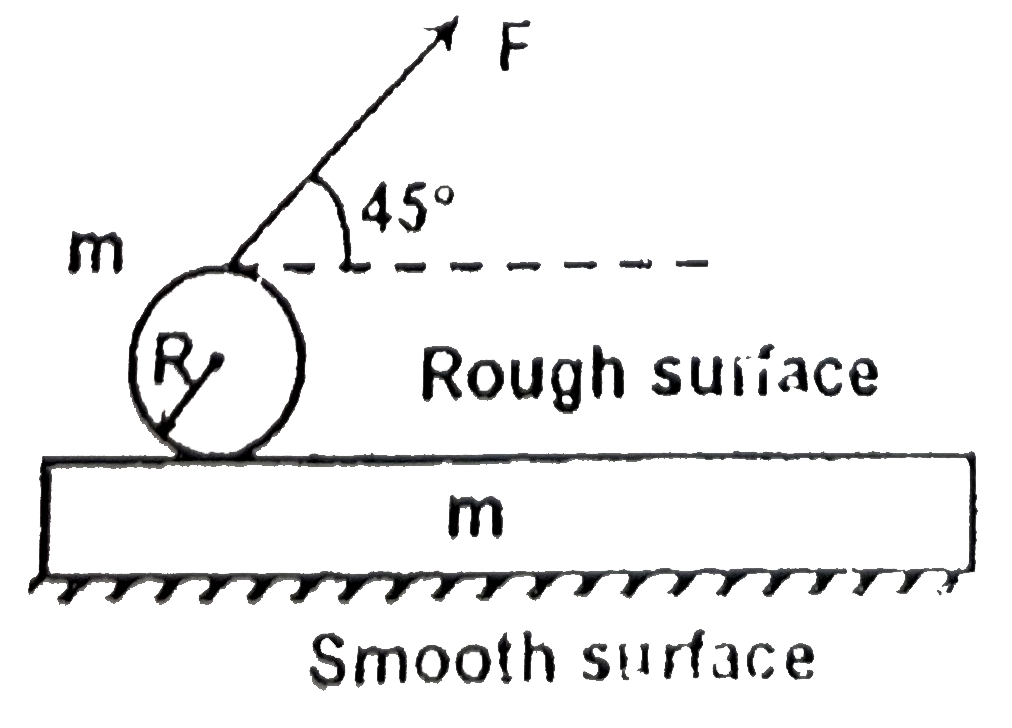
View SolutionA cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View SolutionA cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View SolutionA plank with a uniform sphere placed on it resting on a smooth horizontal plane. Plank is pulled to right by a constant force F. If sphere does not slip over the plank. Which of the following is incorrect?
View Solution
