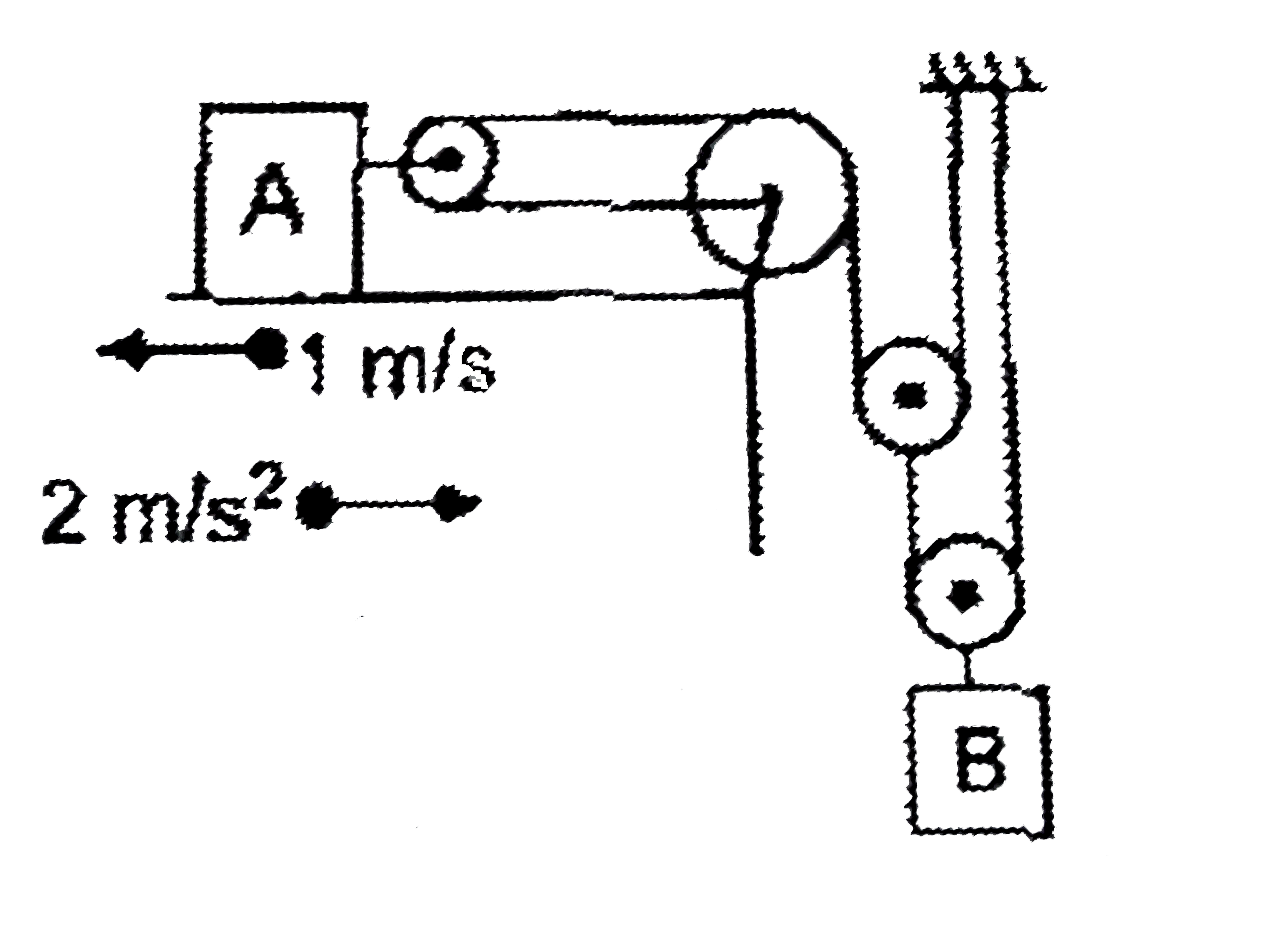
A wheel is rolling on a horizontal plane. At a certain instant it has a velocity v and acceleration a of CM as shown in figure . Acceleration of
A is vertically upwards
B may be vertically down-wards
C cannot be horizontal
some point on the rim may he horizontal leftwards
The correct Answer is:A, B, C, D
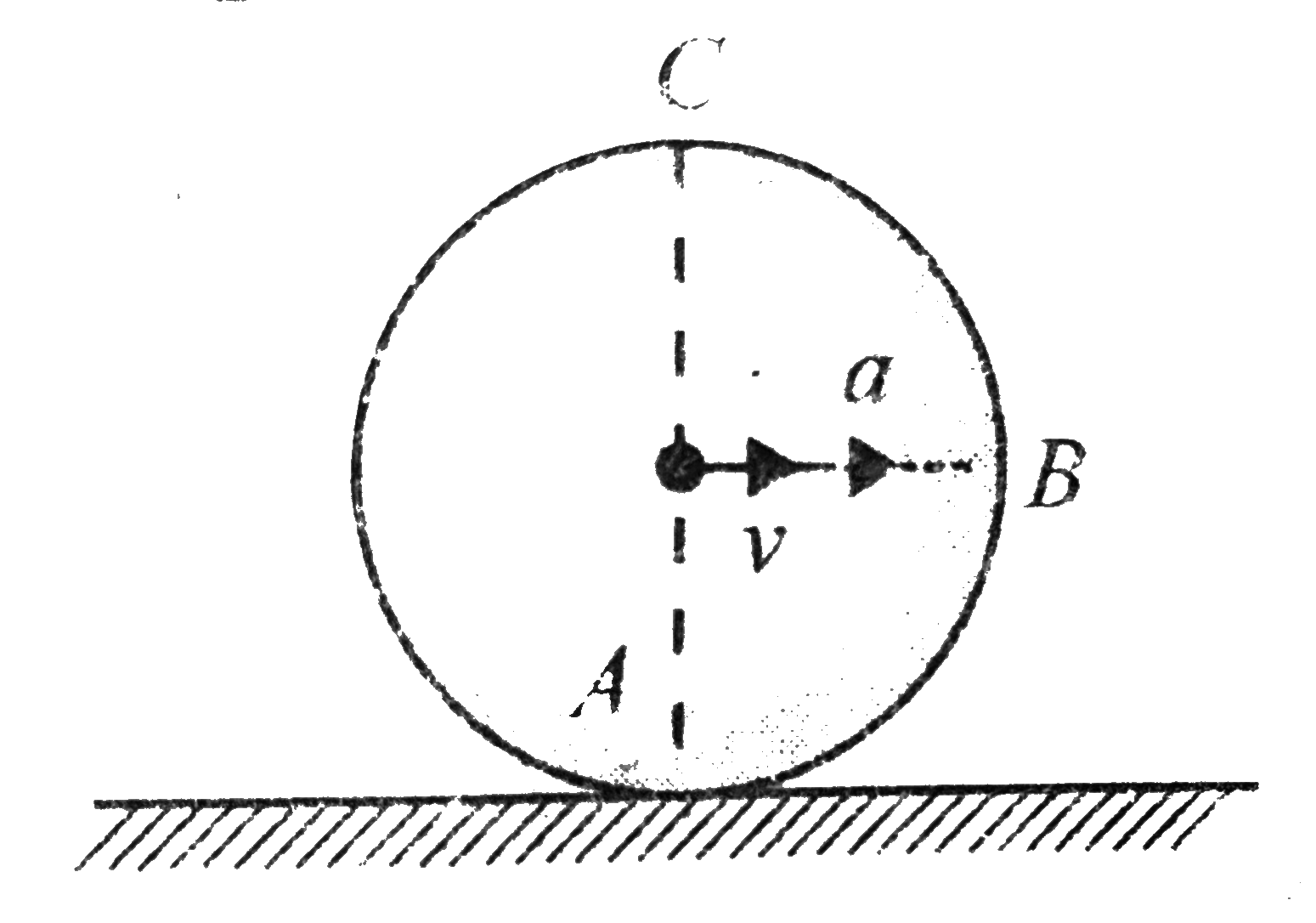
At A:
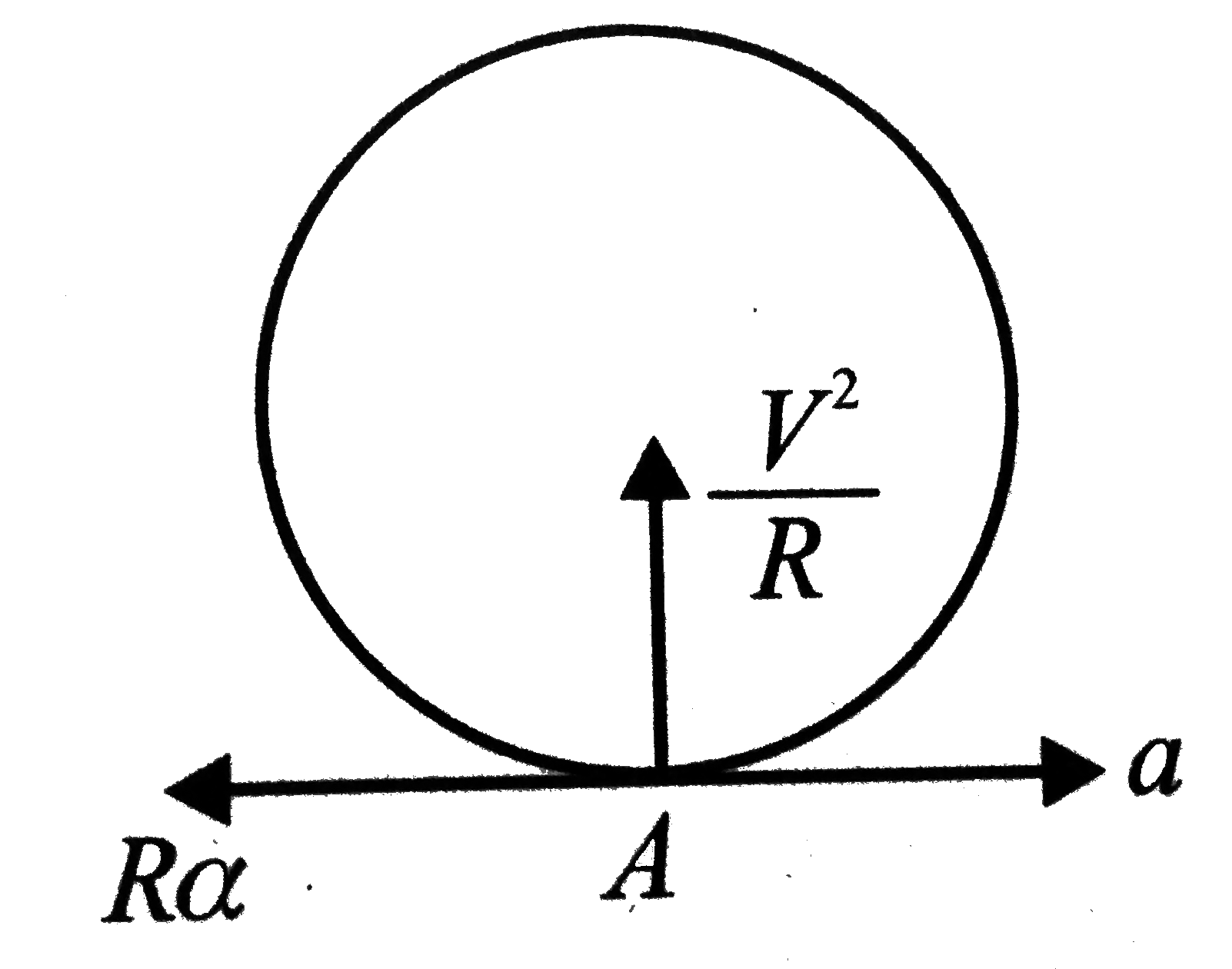
For a rollihng wheel a=Rα
Therefore option a correct. At B:
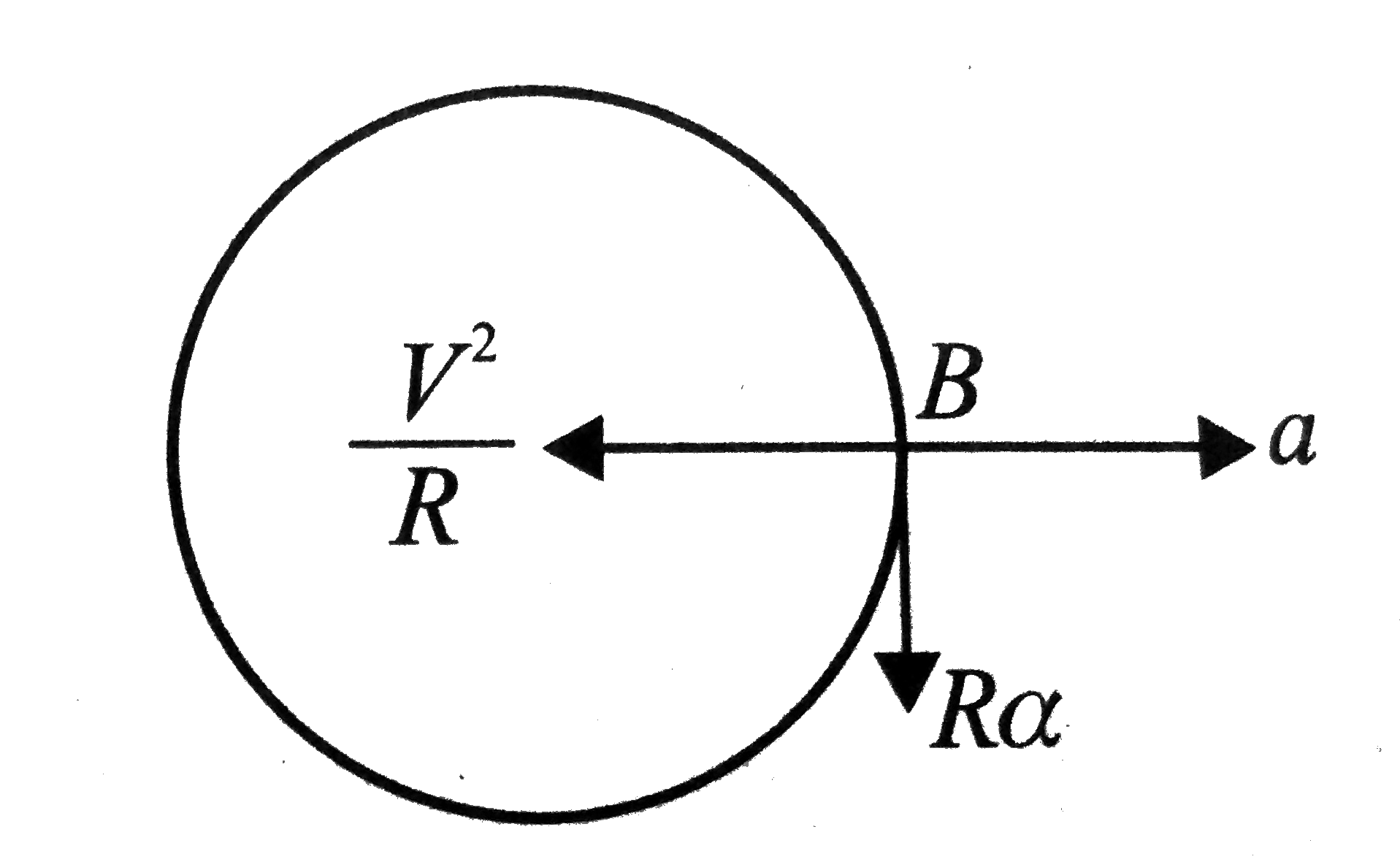
If(V2)r=a then aB may be vertically downwards Therefore, option b correct.
At C:
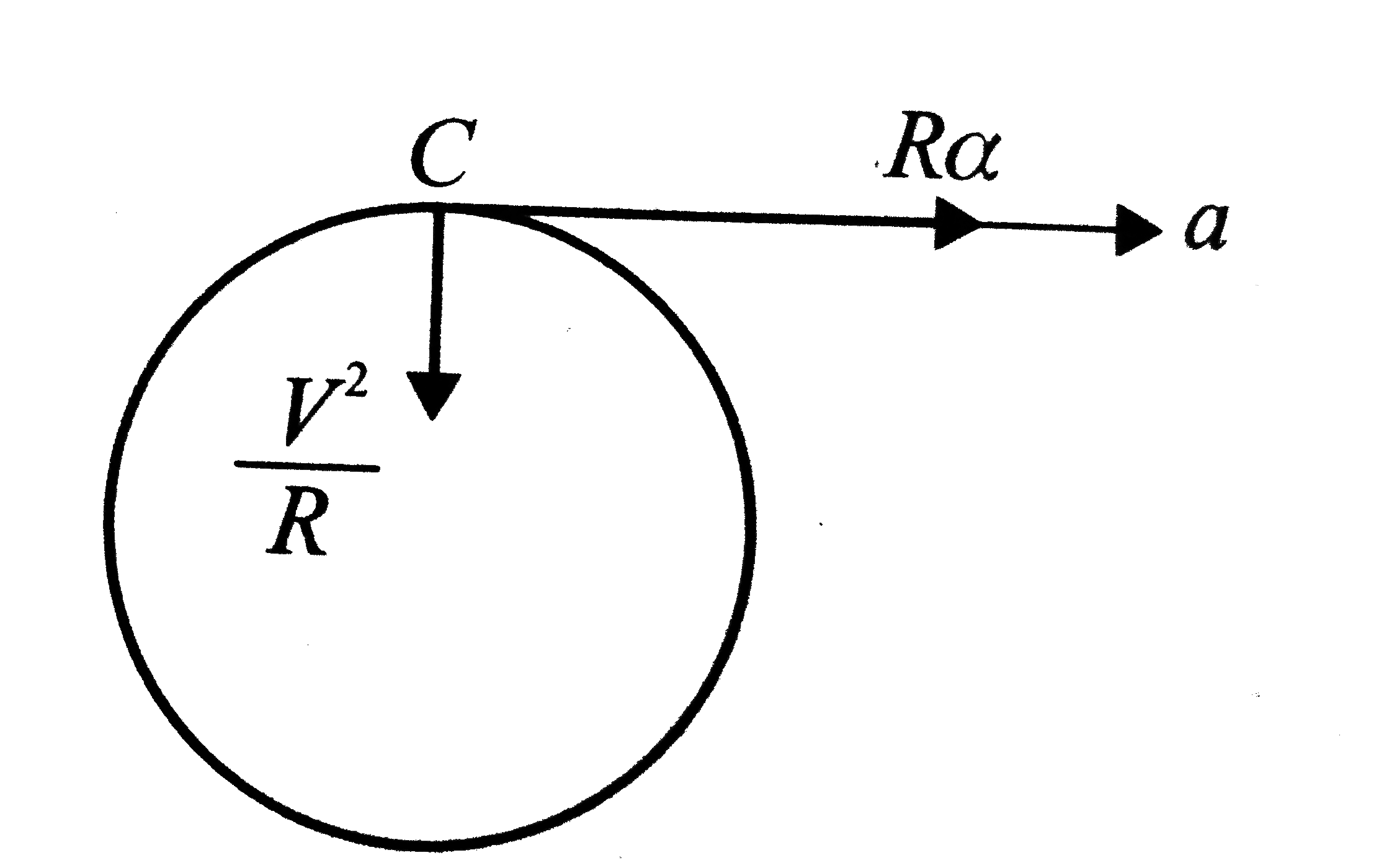
Therfore, option c is correct
Consider this correct

Therfore option d correct.
Similar Questions
Knowledge Check

A wheel is rolling without slipping on a horizontal plane with velocity v and acceleration a of centre of mass as shown in figure. Acceleration atAA is vertically upwardsBB may be vertically downwardsCC cannot be horizontalDA point on the rim may be horizontal leftwards.A disc having radius R is rolling without slipping on a horizontal (x−z) plane. Centre of the disc has a velocity v and acceleration a as shown.
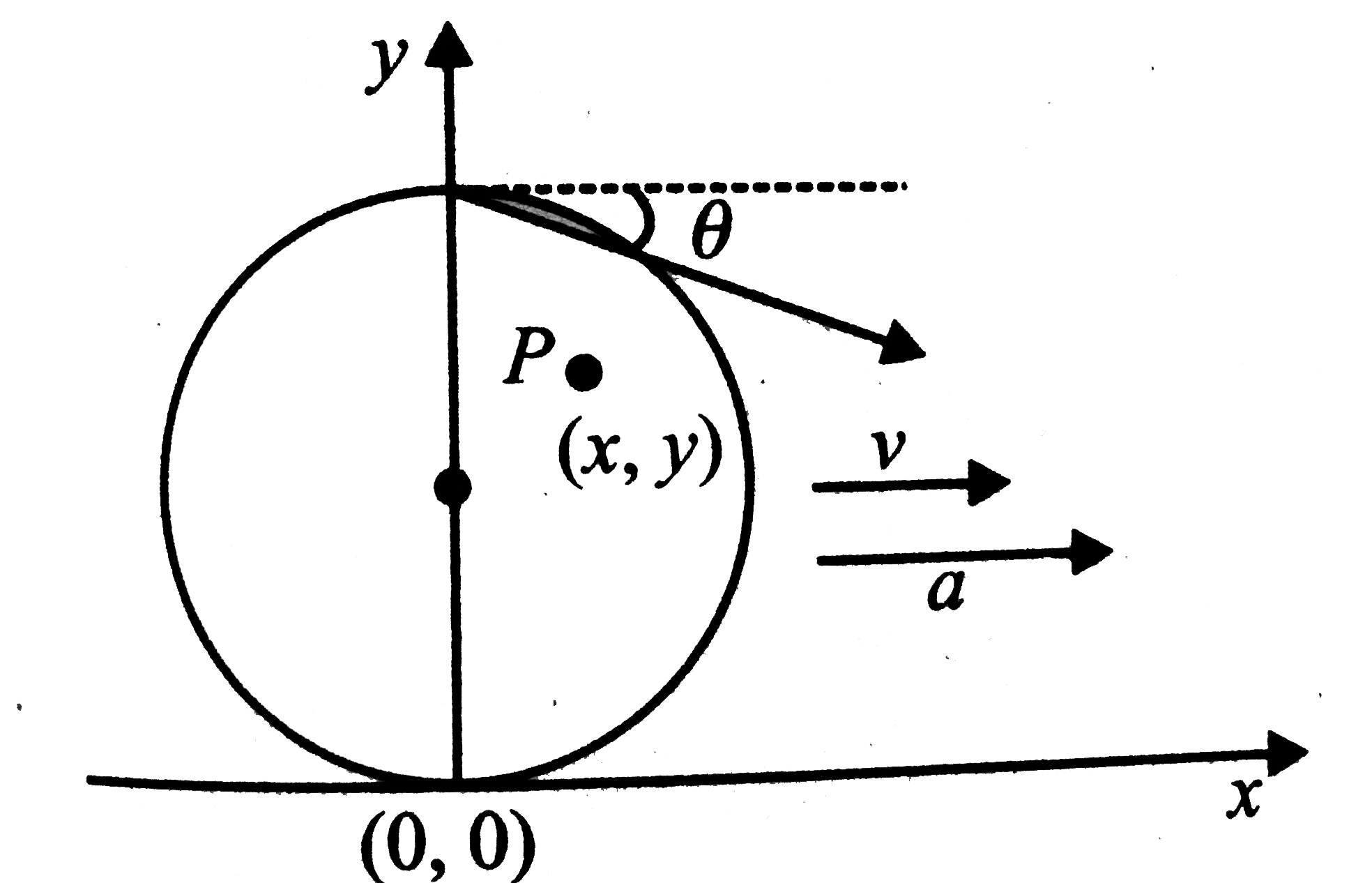
If v=√2aR the angle ρ between acceleration of the top most point and the horizontal isA0B45∘Ctan−1(2)Dtan−1(12)A disc having radius R is rolling without slipping on a horizontal (x−z) plane. Centre of the disc has a velocity v and acceleration a as shown.

Speed of point P having coordinates (x,y) isAv√x2+y2RBv√x2+(y+R)2RCv√x2−(y−R)2RDnone
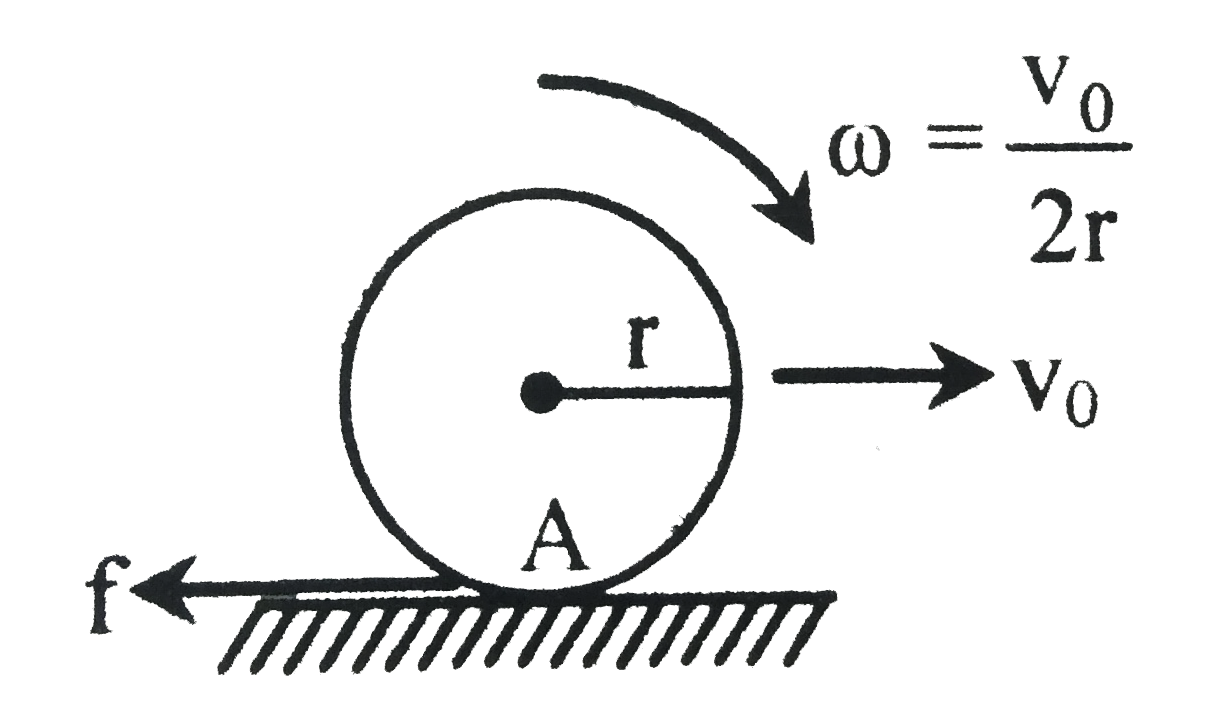
A sphere of mass M and radius r shown in figure slips on a rough horizontal plane. At some instant it has translational velocity V0 and rotational velocity about the centre v02r. Find the translational velocity after the sphere starts pure rolling.
 .
.
View SolutionA ring rotates about z axis as shown in figure. The plane of rotation is xy. At a certain instant the acceleration of a particle P (shown in figure) on the ring is (6ˆi−8ˆj)m/s2. Find the angular acceleration of the ring & the abgular velocity at that instant. Radius of the ring is 2m.

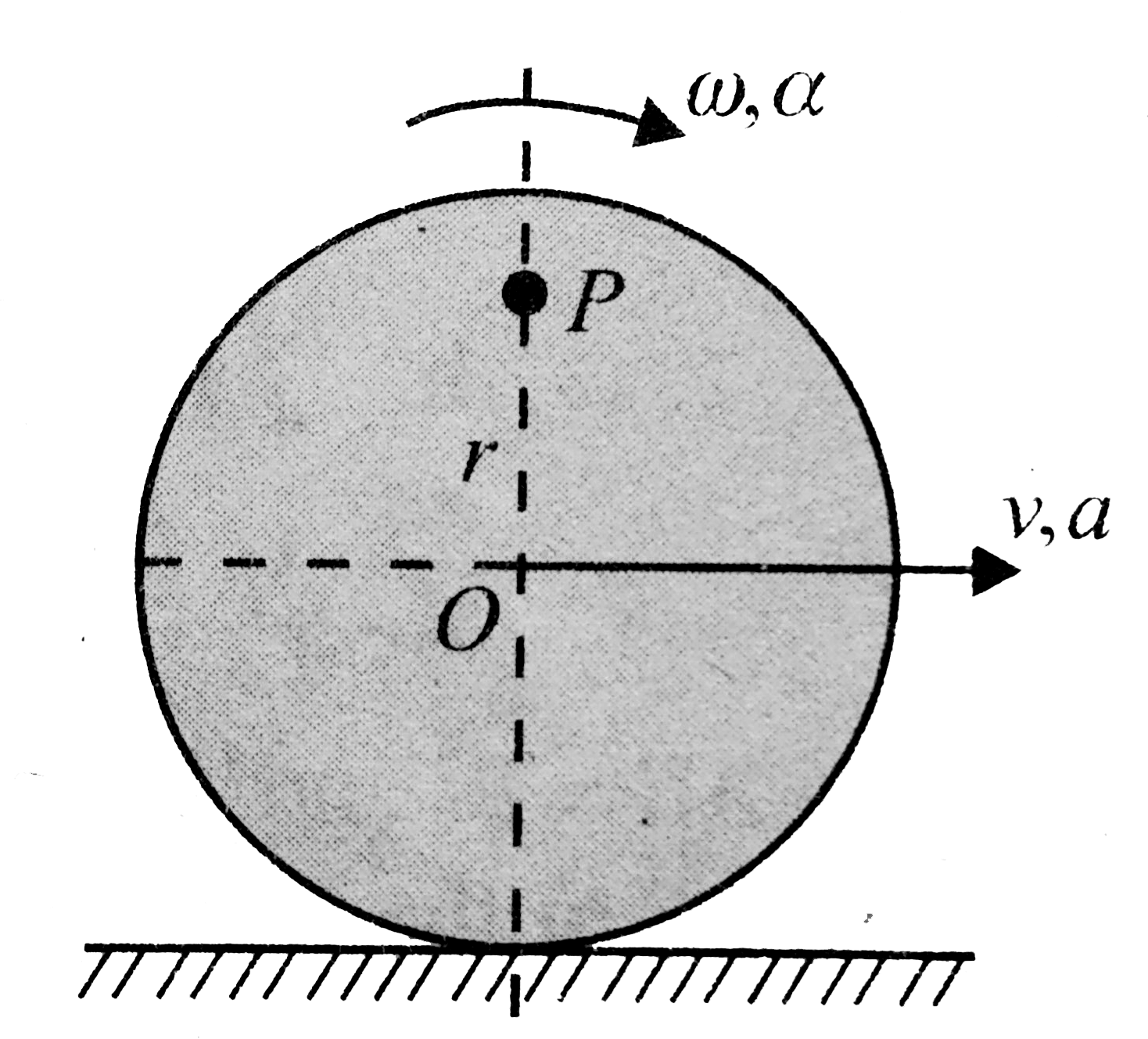
View SolutionA disc of radius R rolls on a horizontal ground with linear acceleration a and angular acceleration α as shown in Fig. The magnitude of acceleration of point P as shown in the figure at an instant when its linear velocity is v and angular velocity is ω will be a
View SolutionA sphere of mass M and radius r shown in the figure on a rough horizontal plane. At some instant it has translational velocity v0, and rotational velocity about centre v0/2r. The percentage change of translational velocity after the sphere start pure rolling:

View Solution
A uniform circular righ rolls without slipping on a horizontal surface. At any instant, its position is as shown in the figure. Then
View Solution


 .
.