A container of large uniform cross sectonal area A, resting on horizontal surface, holds two immiscible non viscous and incompresible liquids of density d and 2d, each of height H2 as shown in the figure. Thelower density liquid is open to the atmospher having presure P0. A tiny hole of area (s(s>>A) is punched on the vertical side of the container at a height h(h>H2). Determine

a.the initial speed of efflux of the liquid at the hole
b. the horizontal disance x travelled by the liquid initially
c. the height hm at which at the hole should be punched so that the liquid travels the maximum distance xm initially. also calculate xm (neglect air resistance inte calculations).
a. Applying Beroulli's theorem at point E ( a point on the interface of the liquids and on the top surface of the liquid of density 2d) and F, i.e, pressure energy = kinetic energy + potential energy = constant
⇒P0+H2dg+12(2d)×0+H2dg
=P0+12(2d)v2+2hdg
⇒32Hdg=dv2+2hdg
⇒v2=32Hg−2hg=(3H−4h)g2
∴v=
⎷{(3H−3h)2g}
Method :2 Let the equivalent depth of liquid 1 of denisty in terms of density 2d which gives the dame pressure as liquid 1 at interface i.e.,
H2dg=H'(2d)g which gives H'=H4
Hence depth depth of the liquid above opening (in terms of depth of liquid of density 2d).
H'+(H2−h)=H4+(H2−h)
Hnet=(3H−4h4)
and velocity of efflux is given by
v=√2ghnet
v=√3H−4h2g
time taken by the liquid to fall through a vertical height h is given by
H=12gt2⇒t=√2hg
Therefore horizontal distance traversed by liquid is
x=vt=√(3H−4h)g2×√2hg
c. For the minimum horizontal distance x
dxdh=0⇒ddh(3Hh−4h2)12=0
or 1293Hh−4h2^(−12)×(3H−8h)=0
this gives 3H−8h−0⇒h=3H8
This is the length of the liquid for which the range is maximum i.e
h→hm=3H8
The maximum horizontal distance is given by
xm=√(3H−3hm)hm
√{(3H−43H3)3H8}9=34H
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Exercise 4.1
Explore 11 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Exercise 4.2
Explore 11 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:INTEGER_TYPE
Explore 1 Video
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
A container of cross-section area A resting on a horizontal surface, holds two immiscible and incompressible liquid of densities ρand2ρ as shown in figure. The lower density liquid is open to the atmosphere having pressure P0. The pressure at the bottom of the container is
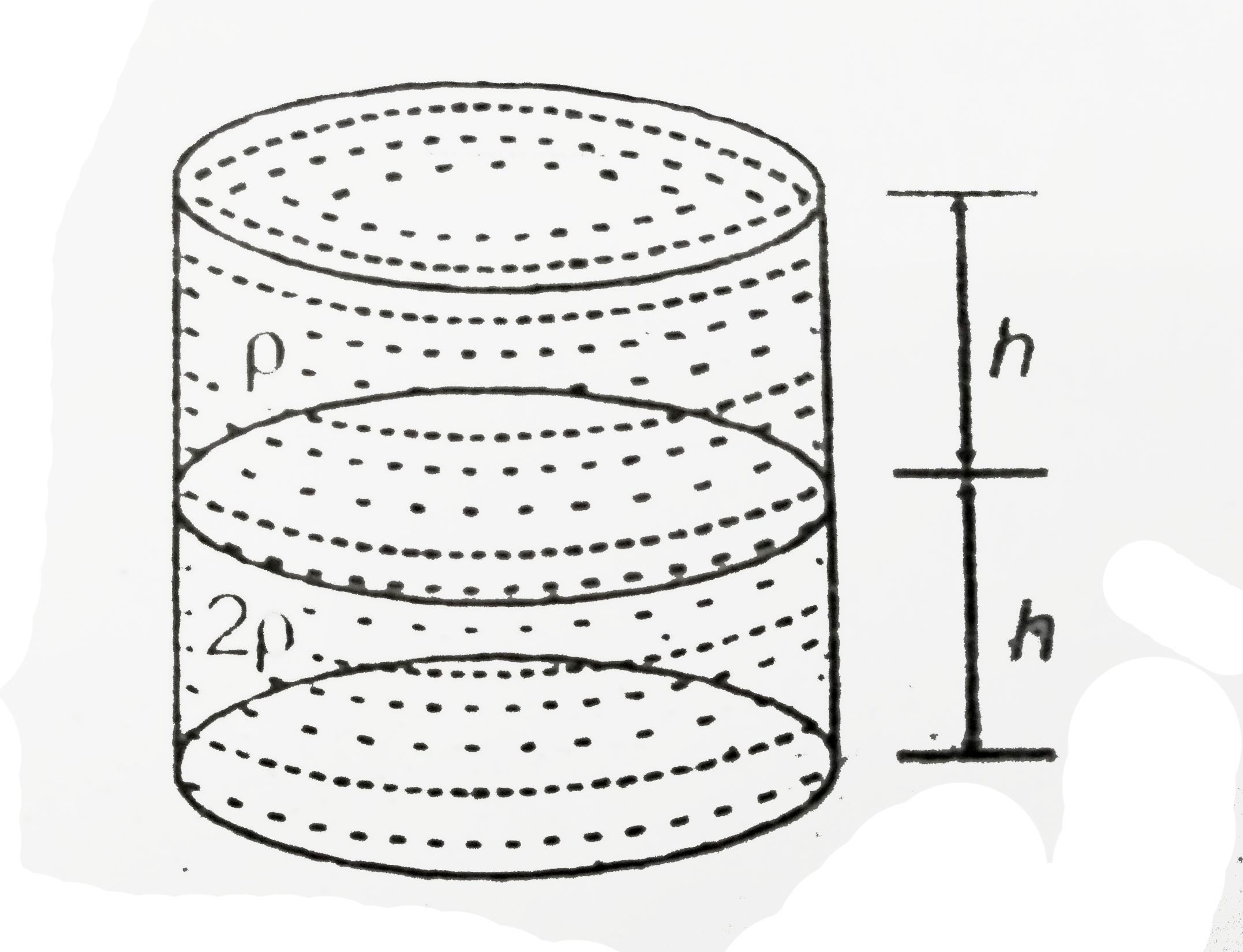
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holds two immiscible, non-viscous and incompressible liquids of densities d and 2d, each of height H2 as shown in figure. The lower density liquid is open to the atmosphere having pressure P0.
(a) A homogeneous solid cylinder of length L(L<H2) cross-sectional area A5 is immersed such taht it floats with its axis vertical at the liquid-liquid interface with the length L4 in the denser liquid. Datermine:

(i) The density D of the solid and
(ii) The total pressure at the bottom of the container.
(b) The cylinder is removed and the original arrangement is restored. A tiny hole of area s(s<<A) is puched on the vertical side of the container at a height h(h−(H2)). Determine :
(i) The initial speed of the efflux of the liquid at the hole
(ii) The horizontal distance x travelled by the liquid initially and
(iii) The height hm at which the hole should be punched so that the liquid travels the maximum distance xm. initially. Also calculate xm. [ Neglect air resistance in these calculations ]

View Solution
Knowledge Check
A container of large uniform cross sectional area A resting on a horizontal surface holds two immiscible non-viscous and incompressible liquids of density d and 3d each of height H/2. The lower density liquid is open to the atmosphere having pressure Po. A tiny hole of area a (a<<A) is punched on the vertical side of the lower container at a height h(0<h<H2) for which range is maximum.
Ah=H/3BRange R=2H/3CRange R=3H/2Dvelocity of efflux r v=√23gHFluids at rest exert a normal force to the walls of the container or to the sruface of the body immersed in the fluid. The pressure exerted by this force at a point inside the liqid is the sum of atmospheric pressure and a factor which depends on the density of the liquid, the acceleration due to gravity and the height of the liquid, above that point. The upthrust acting on a body immersed in a stationary liquid is the net force acting on the body in the upward direction. A number of phenomenon of liquids in motion can be explain by Bernoulli's theorem which relates the pressure, flow speed and height for flow of an ideal incompressible fluid.
A container of large uniform corss sectional area. A resting on a horizontal surface holds two immiscible, non viscous and incompressile liquids of densities d and 2d, each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0.
Situation II:
A cyliner is removed and the original arrangement is restoreed.A tiny hole of area s(s<<A) is punched on the veritical side of the containier at a height h(h<H/2)
The height hm at which the hole should be punched so that the liquid travels the maximum distance isA2H3B3H8C4H3D4H3A container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The density D of the material of the floation cylinder isA5d/4B3d/4C4d/5D4d/3
A container of large uniform cross-sectional area A resting on a horizontal surface, holds two immiscible, non-viscous and incompressible liquids of densities d and 2d, each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0.
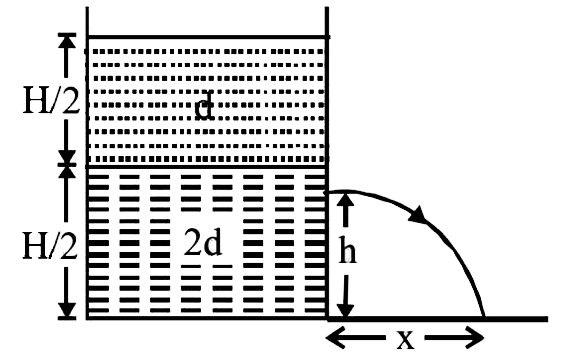
(a) A homogeneous solid cylinder of length L(L<H/2), cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid. Determine:
(i) the density D of the solid and
(ii) the total pressure at the bottom of the container.
(b) The cylinder is removed and the original arrangement is restored. A tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). Determine:
(i) the initial speed of efflux of the liquid at the hole,
(ii) the horizontal distance x travelled by the liquid initially, and
(iii) the height hm at which the hole should be punched so that the liquid travels the maximum distance xm initially. Also calculate xm.
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holds two-immiscible, non-viscous & incompressible liquids of densities d & 2d, each of height H/2. The lower density liquid is open to the atmoshpere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) corss-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid interface with the length L/4 in the denser liquid. Determine : (i) The density D of the solid & (ii) The total pressure at the bottom of the container.
View SolutionA container of a large uniform cross-sectional area A resting on a horizontal surface holds two immiscible, non viscous and incompressible liquids of densities d and 2d, each of height H/2 as shown in figure. The lower density liquid is open to atmosphere. A homogeneous solid cylinder of length L(L<H2), cross-sectional area A/5 is immersed such that it floats with its axis vertical of the liquid-liquid interface with length L/4 denser liquid. Determine
(a) density D of the solid and
(b) the total pressure at the bottom of the container. (Atmospheric pressure =P0).
 .
.
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The total pressure with cylinder, at the bottom of the container is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The initial speed of efflux without cylinder is
View Solution
