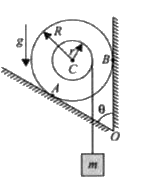
A massless spool of inner radius r outer radius R is placed against a vertical wall and a titled split floor as shown. A light inextensible thread is tightly wound around the spool through which a mass m is hainging. There exists no friction at point A, while the coefficient of friction between the spool and point B is μ. The angle between the two surface is ρ

The magnitude of the force on the spool at B in order to maintain equilibrium is mg√(rR)2+(1−rR)21tan2θ
The magnitude of the force on the spool at B in order to maintain equilibrum is mg(1−rR)1tanθ
The minimum value of μ for the system to remain in equilibrium is cotθ(R/r)−1
The minimum values of μ for the system to remain in equilibrium is tanθ(R/r)−1
The correct Answer is:A, D
mgr=fR………..i
N1sinθ+f=mg ………………ii
N1cosθ=N2……………..iii

From eqn i. f=mgrR
From eqn ii and iii N2=mg−ftanθ=mgtanθ[1−rR]
Net force at B:fB=√f2+N22
For the minimum value of μ:f≤μN2
⇒mgrr≤μmgtanθ[1r/R]
⇒μ≥tanθR/r−1)
Similar Questions
A spool of mass m has moment of inertia I=2mR2 about its axis of symmetry. The inner and outer radius of spool R and 2R respectively. Thread is wounded on the inner cylinder and its one end is pulled a force F acting at angle θ with horizontal. The surface is sufficiently rough and th.e spool never slides on the surface.

Regarding to the direction of rotation of spool which of the following statement is true?
View SolutionA spool of mass m has moment of inertia I=2mR2 about its axis of symmetry. The inner and outer radius of spool R and 2R respectively. Thread is wounded on the inner cylinder and its one end is pulled a force F acting at angle θ with horizontal. The surface is sufficiently rough and th.e spool never slides on the surface.

Maximum frictional force acting on the spool is:
View SolutionA spool has a mass of 2 kg,an inner radius R_(1) =3cm,and an outer radius R_(2)= "5cm, the radius of gyration about the axis of the spool is if" =4cm .A constant horizontal force of 5N is applied to the free end of a massless thread that is wrapped around the inner cylinder of the spool as shownin figure-5.150. If the spool rolls without slipping, calculate the linear acceleration along the horizontal surface. What is the minimum coefficient of static friction required to prevent slipping ?
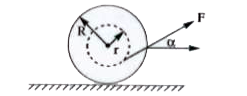
View SolutionInner and outer radii of a spool are r And R respectively. A thread is wound over ita ineer surface and placed over a rough horizontal surface. Thread is pulled by a force F as shown in the figure. Then in case of pure rolling.

View SolutionA massless spool of inner radius r, outer radius R is placed against vertical wall and tilted split floor as shown. A light inextensible thread is tightly wound around the spool through which a mass m is hanging. There exists no friction at point A, while the coefficient of friction between spool and point B is μ . The angle between two surface is θ.
View SolutionInner and outer radii of a spool are r and R, respectively. A thread is wound over its inner surface and spool is placed over a rough horizontal surface. Thread is pulled by a force F as shown in Figure. In case of pure rolling, which of the following statements are possible to be correct
View SolutionThe figure shows a spool placed at rest on a horizontal rough surface. A tightly wound string on the inner cylinder is pulled horizontally with a force F. identify the correct alternative related to the friction f acting on the spool
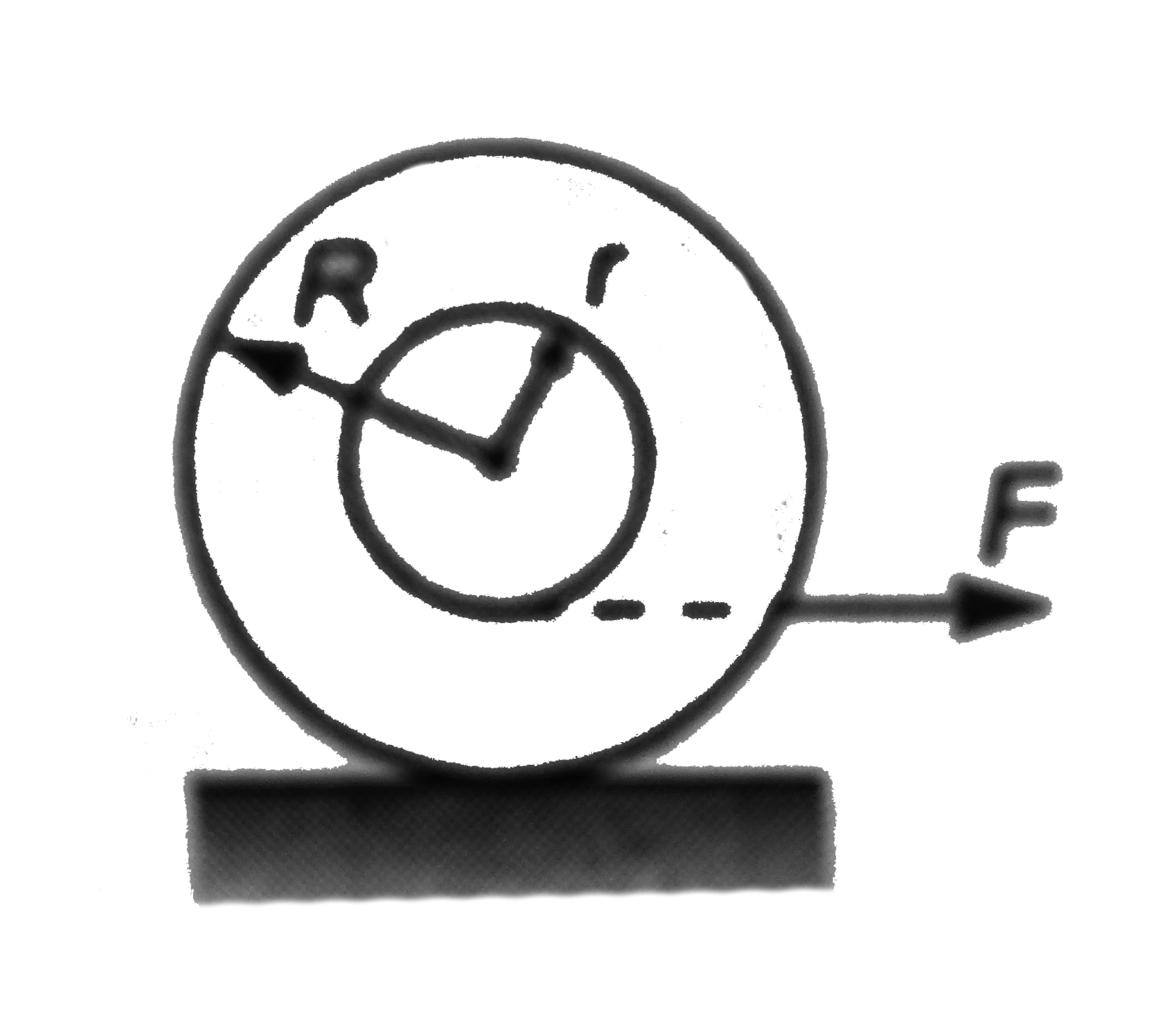
View SolutionA massless spool of inner radius r outer radius R is placed against a vertical wall and a titled split floor as shown. A light inextensible thread is tightly wound around the spool through which a mass m is hainging. There exists no friction at point A , while the coefficient of friction between the spool and point B is mu . The angle between the two surface is theta
View Solution

