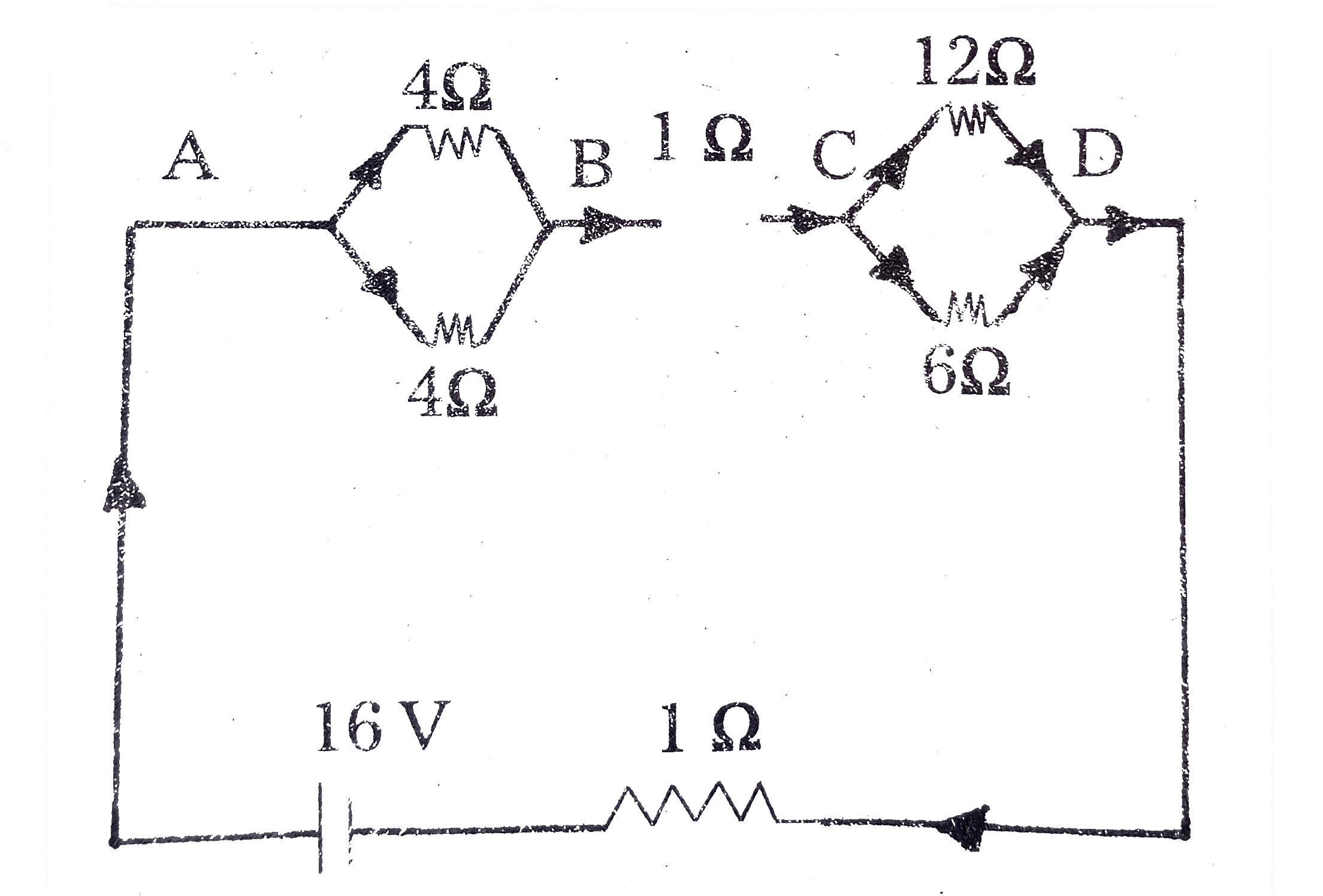
A network of resistor is connected to a 16 V battery with internal resistance of 1Ω, a shown in fig.
(a) complete the equivalent resistance of the network.
 Solution in Telugu
Solution in Telugu
The network is a simple series and parallel combination of resistors. First the two 4Ω resistors in parallel are equivalent to a resistor.
=[(4×4)/(4+4)]Ω=2Ω
In the same, way, the 12Ω and 6Ω resistors in parallel are equivalent to a resistor of
[(12×6)/(12+6)]Ω=4Ω
The equivalent resistance R of the network is obtained by combining these resistors (2Ω and 4Ω with 1Ω in series, that is
R=2Ω+4Ω+1Ω=7Ω
Similar Questions
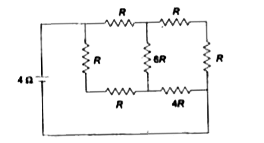
A battery of internal resistance 4Omega is connected to the network of resistances as shown in the fig. In order that the maximum power can be delivered to the network, the value of R in Omega should be
View SolutionA network of Resistors is Connected to a 16V battery with internal resistance 1Omega as shown in Figure below. (a) Compute the equivalent resistance of the network (b) Calculate the total current in the circuit
View SolutionA battery of internal resistance 4Ω is connected to the network of resistances as shown in the fig. In order that the maximum power can be delivered to the network, the value of R in Ω should be

View SolutionA network of resistors is connected to a 12V battery as shown in fig.
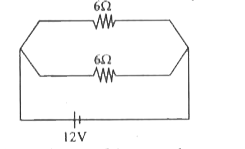
a) Calculate the equivalent resistance of the network.
b) Obtain current in 12Ω and 6Ω resistors.
View SolutionA network of resistances is connected to a 16V battery with internal resistance of 1 Omega as shown in Fig. Compute the equivalent resistance of the network
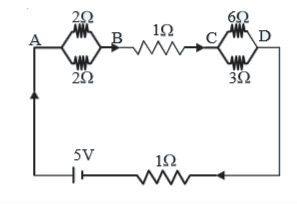
View SolutionA network of resistors is connected to a 5 V battery with internal resistance of 1Ω as shown in Fig. (a) Compute the equivalent resistance of the network. (6) Obtain the current in each resistor. (c) Obtain the voltage drops VBC and VCD
View SolutionA battery of internal resistance 4 Ω is connected to the network or resistances as shown in Fig. In order that maximum power cab be delivered to the network, the value of R in ohm should be
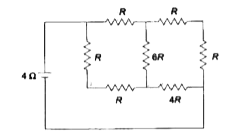
View SolutionA battery of internal resistance 4Ω is connected to the network of resistances as shown in Fig. In order that maximum power can be delivered to the network, the value of R in ohm should be:
View Solution

