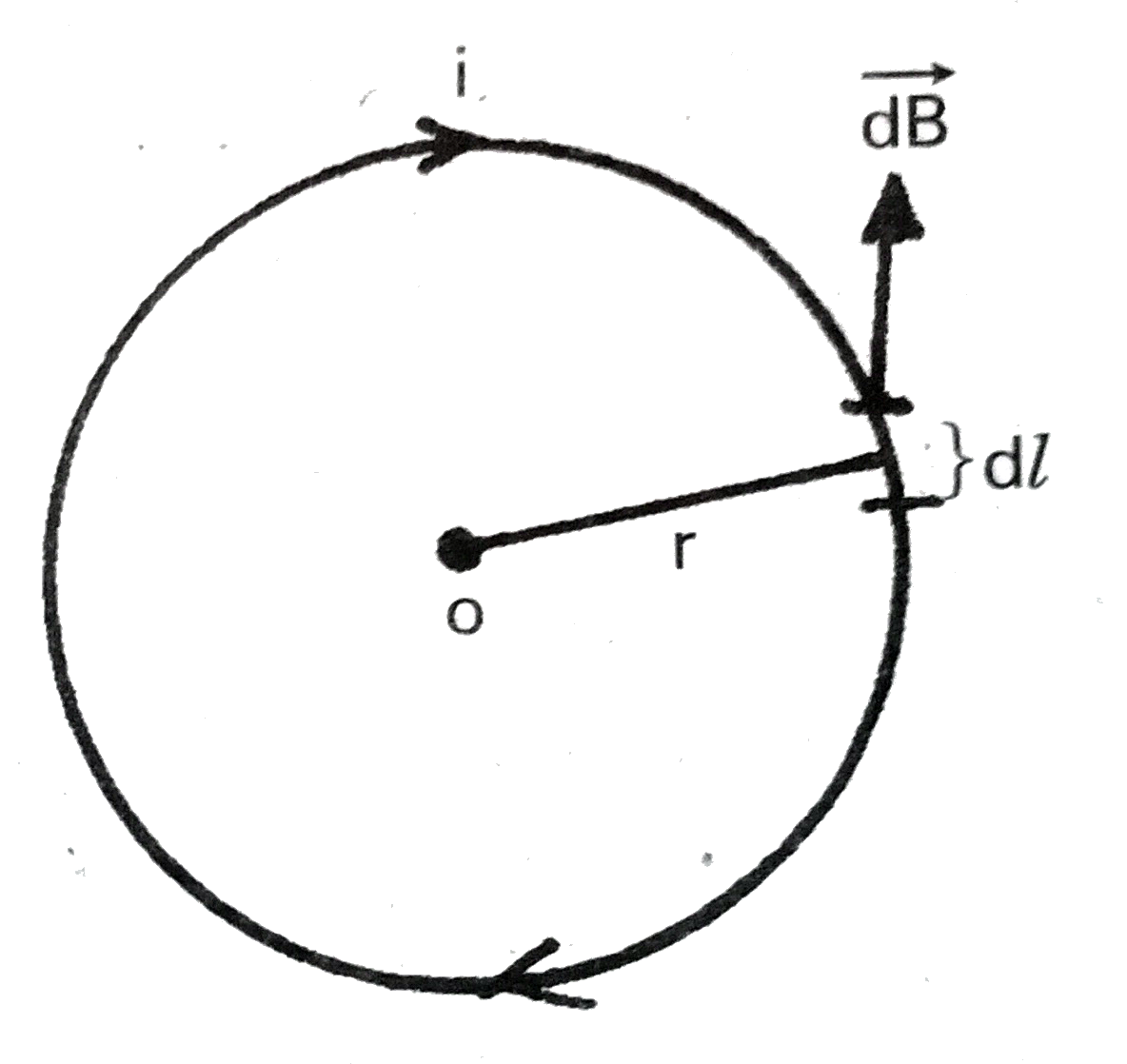
Derive an expression for the magnetic induction at the centre of a current carrying circular coil using Biot-Savart law. Solution in Telugu
Consider a circular coil of radius r and carry a current i. Consider a small element 'dl'. Let O is the centre of the coil. By using Biot- Savart's law
dB=μ04π.Idlsinθr2
Here angle →dland→r is 90∘(i.e.θ=90∘)
dB=μ04πidlr2→(1)
As the field due to all elements of the circular loop have the same direction.
The resultant magnetic field can be obtained by integrating equation (1)
∫dB=∫μ04π.idlr2
B=μ0i4πr2∫dl ∵(∫dl=2πr)
=μ0i4πr2×2πr
B=μ0i2r
If the circular coil has n turns.
B=μ0ni2r
Similar Questions
State Biot-Savart law, giving the mathematical expression for it.
Use this law to derive the expression for the magnetic field due to a circular coil carrying current at a point along its axis.
How does a circular loop carrying curent behave as a magnet?
View SolutionUse Biot-Savart law to derive the expression for the magnetic field on the axis of a current carrying circular loop of radius R . Draw the magnetic field lines due to circular wire carrying current I .
View Solution(a) State Biot - Savart law and ecpress it in the vector form.
(b) Using Biot - Savart law, law obtain the expression for the magnetic field due to a circular coil of radius r, carrying a current I at point on its axis distant x from the centre of the coil.
View SolutionUsing Biot-Savart's law, derive an expression for magnetic field at the centre of a current carrying circular coil. What will be the direction of this magnetic field?
View SolutionDerive an expression for magnetic field at the centre of circular current carrying coil.
View Solution(A) : The magnetic field at the centre of a circular coil carrying current could be calculated using Amperes circuital law. (R) : Biot savart law could be derived from Amperes law.
View SolutionUsing Biot-Savart's law, derive an expression for the magnetic field at the center of a circular coil carrying current
View SolutionState Biot Savarts law. Write down the expression of magnetic field at the centre of a current carrying circular coil of N turns.
View Solution
