Two identical small charged spheres, each having a mass m, hang in equilibrium as shown in fig. the ligth of each string is l, and the angle made by any string with the vertical is θ. Find the magnitude of the charge on each sphere.
To solve the problem of finding the magnitude of the charge on each of the two identical small charged spheres hanging in equilibrium, we can follow these steps:
1. Identify the Forces Acting on the Spheres:
Each sphere experiences three main forces:
- The gravitational force (weight) acting downward: Fg=mg
- The tension in the string (T) acting along the string at an angle θ to the vertical.
- The electrostatic force (F) due to the repulsion between the two charged spheres.
2. Resolve the Tension into Components:
The tension T can be resolved into two components:
- Vertical component: Tcosθ
- Horizontal component: Tsinθ
3. Set Up the Equilibrium Conditions:
Since the spheres are in equilibrium:
- In the vertical direction:
Tcosθ=mg(1)
- In the horizontal direction:
Tsinθ=F(2)
where F is the electrostatic force between the two charges.
4. Calculate the Electrostatic Force:
The electrostatic force between two point charges is given by Coulomb's law:
F=kq2r2
where k is Coulomb's constant, q is the charge on each sphere, and r is the distance between the two spheres.
5. Determine the Distance r:
The distance r between the two spheres can be expressed in terms of the length of the string l and the angle θ:
r=2lsinθ
6. Substitute r into the Electrostatic Force Equation:
Substituting r into the expression for F:
F=kq2(2lsinθ)2=kq24l2sin2θ(3)
7. Combine Equations (1) and (2):
From equations (1) and (2), we can express F in terms of mg:
Tsinθ=kq24l2sin2θ
Using T=mgcosθ from equation (1), we can substitute T into the equation:
mgcosθsinθ=kq24l2sin2θ
8. Rearranging the Equation:
Rearranging gives:
mgtanθ=kq24l2sin2θ
9. Solve for q2:
Rearranging for q2:
q2=4l2sin2θ⋅mgtanθk
10. Final Expression for q:
Taking the square root gives:
q=√4l2sin2θ⋅mgtanθk
Final Answer:
q=2lsinθ√mgtanθ√k
Each sphere experiences three main forces:
- The gravitational force (weight) acting downward: Fg=mg
- The tension in the string (T) acting along the string at an angle θ to the vertical.
- The electrostatic force (F) due to the repulsion between the two charged spheres.
The tension T can be resolved into two components:
- Vertical component: Tcosθ
- Horizontal component: Tsinθ
Since the spheres are in equilibrium:
- In the vertical direction:
Tcosθ=mg(1)
- In the horizontal direction:
Tsinθ=F(2)
where F is the electrostatic force between the two charges.
The electrostatic force between two point charges is given by Coulomb's law:
F=kq2r2
where k is Coulomb's constant, q is the charge on each sphere, and r is the distance between the two spheres.
The distance r between the two spheres can be expressed in terms of the length of the string l and the angle θ:
r=2lsinθ
Substituting r into the expression for F:
F=kq2(2lsinθ)2=kq24l2sin2θ(3)
From equations (1) and (2), we can express F in terms of mg:
Tsinθ=kq24l2sin2θ
Using T=mgcosθ from equation (1), we can substitute T into the equation:
mgcosθsinθ=kq24l2sin2θ
Rearranging gives:
mgtanθ=kq24l2sin2θ
Rearranging for q2:
q2=4l2sin2θ⋅mgtanθk
Taking the square root gives:
q=√4l2sin2θ⋅mgtanθk
q=2lsinθ√mgtanθ√k
Similar Questions
Two identical, small, charged spheres, each having a mass of 4.0×10−2kg hang in equilibrium as shown in Fig. 22-10a. The length of each string is 1.5m and the angle θ is 37.0∘. Find the magnitude of the charge on each sphere.
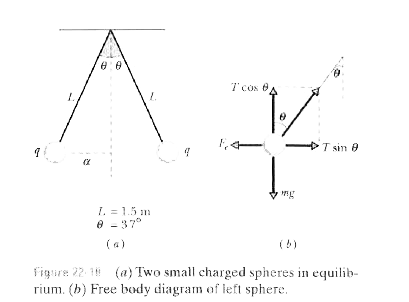
View SolutionTwo identically charged spherical objects are suspended from a common point , using two different threads of equal length. Due to repulsion between charges both strings are maintaining a constant angle with the vertical, and both the objects are in equilibrium. Use m as mass , L as length of each thread. The angle made by each thread with the vertical is θ. Calculate the charge on objects.
View Solution
Knowledge Check
Three identical point charges, each of mass m and charge q, hang from three strings as shown in fig. The value of q in term of m, L, and q is
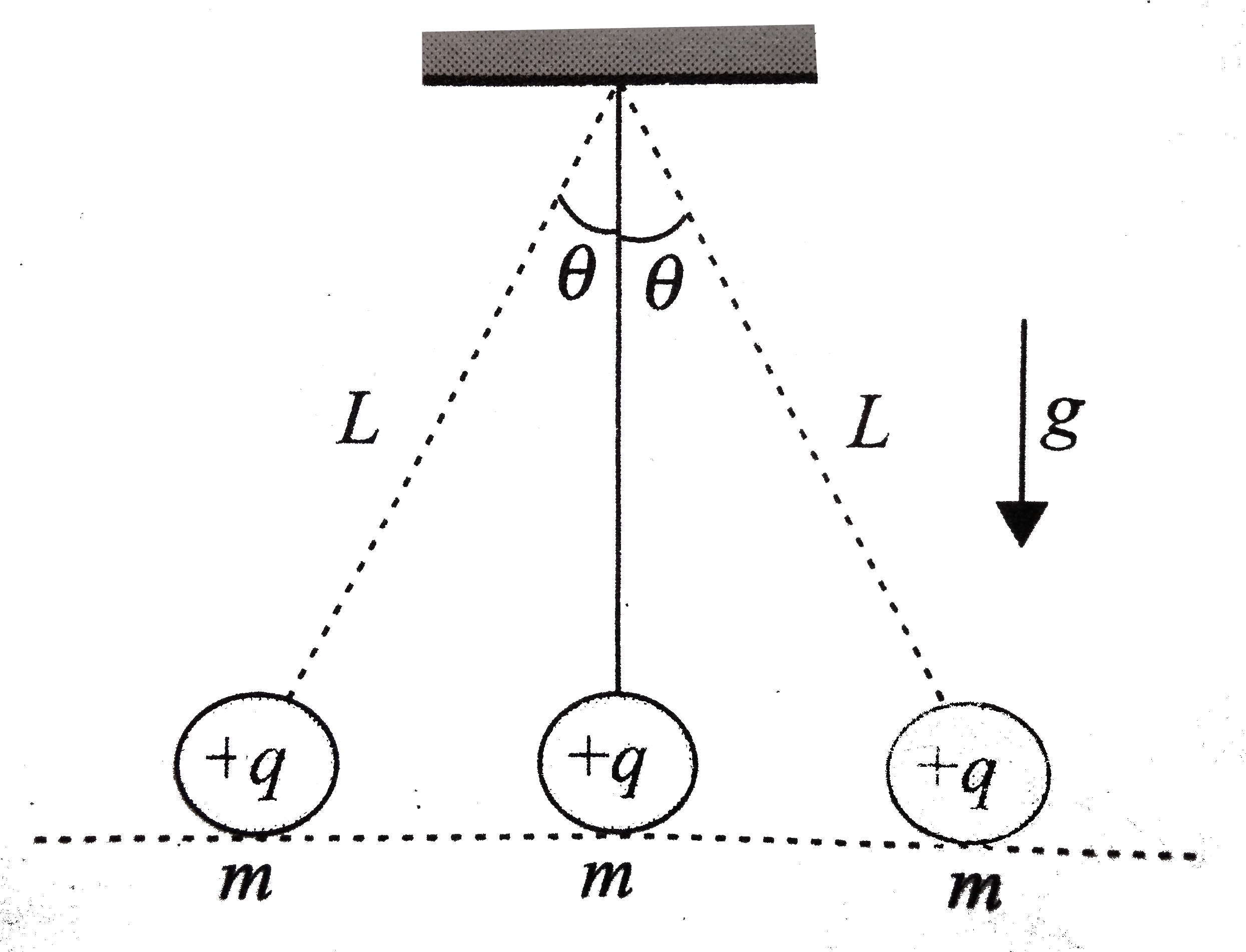 Aq=√(16/5)πε0mgL2sin2θtanθBq=√(16/15)πε0mgL2sin2θtanθCq=√(15/16)πε0mgL2sin2θtanθDnone of these
Aq=√(16/5)πε0mgL2sin2θtanθBq=√(16/15)πε0mgL2sin2θtanθCq=√(15/16)πε0mgL2sin2θtanθDnone of these
Two identical point charges q of mass m each are suspended through strings of equal length l from a common point of suspension. Find the charge q if angle subtended by the strings with the vertical is θ, when point charges are in a state of equilibrium.
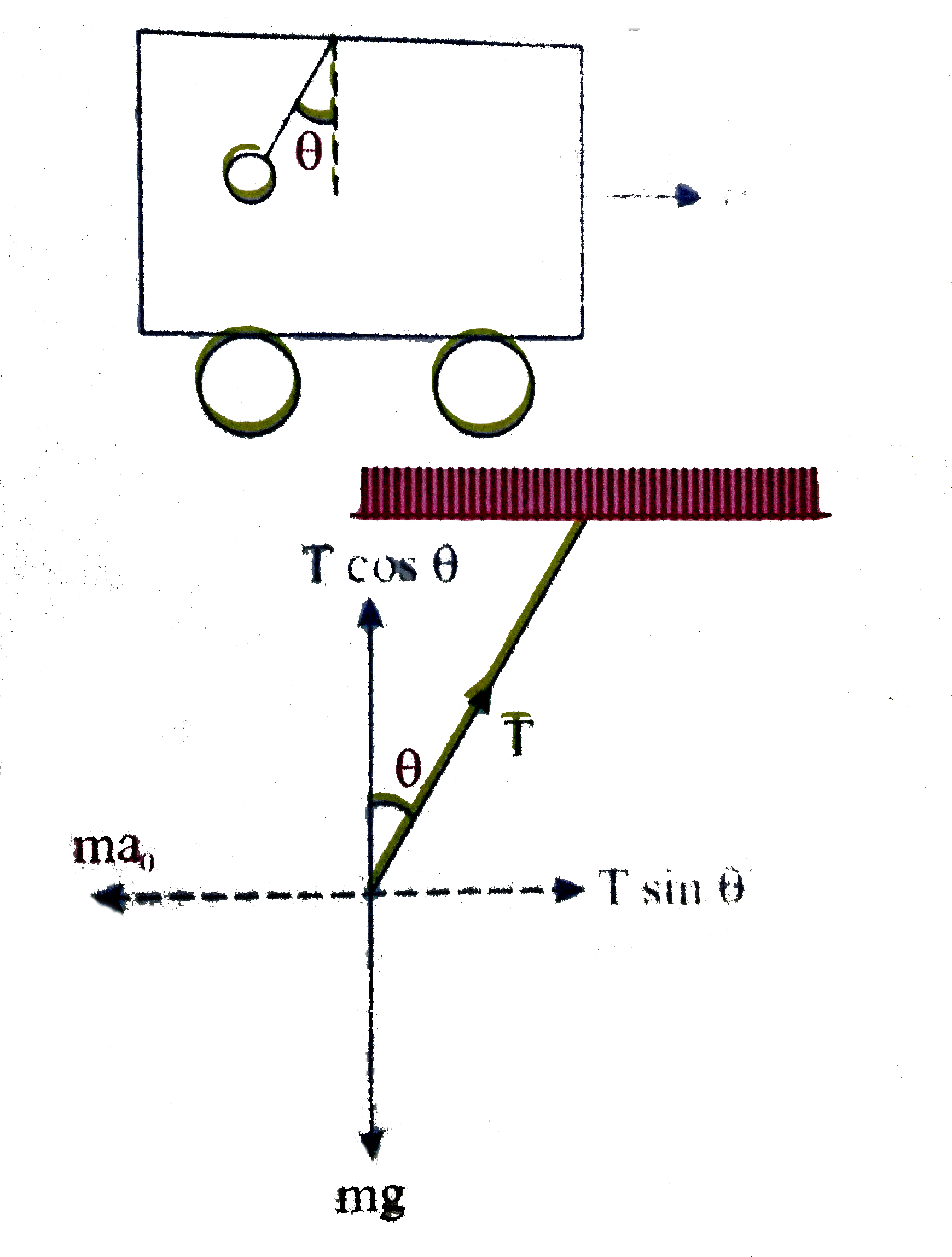
View SolutionA pendulum is hanging from the ceiling of a car having an acceleration a0 with respect to the road. Findthe angle made by the string with the vertical.
View SolutionA small object is suspended at rest from two strings as shown in fig. The magnitude of the force exerted by each string on the object is 10√2N. Find the magnitude of the mass of the object.

View SolutionTwo idential pith balls , each of mass m and charge +q. are suspended from a point with threads of length l each. If in equiilbrium state θ be the angle which each thread makes with vertical in equilibrium , find value of charge on each ball.
View SolutionTwo identical ladders, each of mass M and length L are resting on the rough horizontal surface as shown in the figure. A block of mass m hangs from P. if the system is in equilibrium, find the magnitude and the direction of frictional force at A and B.
View SolutionThree uniform spheres, each having a mass M=5kg and radius a=2.5m are kept in such a way that each touches the other two. Find the magnitude of the gravitational force in GN on any of the spheres due to the other two.
View SolutionA pedulum is hanging from the ceiling of a car having an acceleration a0 with respect to the road Find the angle made by the string with vertical at equilibrium Also find the tension in the string in this position
 .
.
View Solution

