Two fixed point charges +4e and +e units are separated by a distance a. Where should a third point charge be placed for it to be in equilibrium?
To find the position where a third point charge should be placed for it to be in equilibrium between two fixed point charges +4e and +e separated by a distance a, we can follow these steps:
Step 1: Understand the Configuration
We have two fixed charges:
- Charge Q1=+4e located at point A.
- Charge Q2=+e located at point B, a distance a away from Q1.
We need to place a third charge Q such that the net force acting on it due to Q1 and Q2 is zero.
Step 2: Identify Possible Positions for Charge Q
The third charge Q can be placed:
1. Between Q1 and Q2.
2. To the left of Q1.
3. To the right of Q2.
Step 3: Analyze the Forces
1. Between Q1 and Q2:
- Let the distance from Q1 to Q be x.
- Then the distance from Q2 to Q will be a−x.
2. Force Calculations:
- The force F1 acting on Q due to Q1 is given by:
F1=k|Q⋅Q1|x2=kQ⋅4ex2
- The force F2 acting on Q due to Q2 is given by:
F2=k|Q⋅Q2|(a−x)2=kQ⋅e(a−x)2
Step 4: Set Forces Equal for Equilibrium
For the charge Q to be in equilibrium, the magnitudes of the forces must be equal:
F1=F2
This gives us:
kQ⋅4ex2=kQ⋅e(a−x)2
We can cancel k and Q (assuming Q≠0):
4ex2=e(a−x)2
Dividing both sides by e:
4x2=1(a−x)2
Step 5: Cross Multiply and Solve
Cross multiplying gives:
4(a−x)2=x2
Expanding the left side:
4(a2−2ax+x2)=x2
This simplifies to:
4a2−8ax+4x2=x2
Rearranging gives:
3x2−8ax+4a2=0
Step 6: Apply the Quadratic Formula
Using the quadratic formula x=−b±√b2−4ac2a:
Here, a=3,b=−8a,c=4a2:
x=8a±√(−8a)2−4⋅3⋅4a22⋅3
Calculating the discriminant:
x=8a±√64a2−48a26=8a±√16a26=8a±4a6
Step 7: Find the Two Possible Values for x
1. x=12a6=2a (not valid as it exceeds a)
2. x=4a6=2a3
Conclusion
The third charge should be placed at a distance 2a3 from Q1 (or a3 from Q2) for it to be in equilibrium.
We have two fixed charges:
- Charge Q1=+4e located at point A.
- Charge Q2=+e located at point B, a distance a away from Q1.
The third charge Q can be placed:
1. Between Q1 and Q2.
2. To the left of Q1.
3. To the right of Q2.
1. Between Q1 and Q2:
- Let the distance from Q1 to Q be x.
- Then the distance from Q2 to Q will be a−x.
- The force F1 acting on Q due to Q1 is given by:
F1=k|Q⋅Q1|x2=kQ⋅4ex2
- The force F2 acting on Q due to Q2 is given by:
F2=k|Q⋅Q2|(a−x)2=kQ⋅e(a−x)2
For the charge Q to be in equilibrium, the magnitudes of the forces must be equal:
F1=F2
This gives us:
kQ⋅4ex2=kQ⋅e(a−x)2
We can cancel k and Q (assuming Q≠0):
4ex2=e(a−x)2
Dividing both sides by e:
4x2=1(a−x)2
Cross multiplying gives:
4(a−x)2=x2
Expanding the left side:
4(a2−2ax+x2)=x2
This simplifies to:
4a2−8ax+4x2=x2
Rearranging gives:
3x2−8ax+4a2=0
Using the quadratic formula x=−b±√b2−4ac2a:
Here, a=3,b=−8a,c=4a2:
x=8a±√(−8a)2−4⋅3⋅4a22⋅3
Calculating the discriminant:
x=8a±√64a2−48a26=8a±√16a26=8a±4a6
1. x=12a6=2a (not valid as it exceeds a)
2. x=4a6=2a3
The third charge should be placed at a distance 2a3 from Q1 (or a3 from Q2) for it to be in equilibrium.
Similar Questions
Two fixed charges are as shown. Where should the third charge be placed so that its in equilibrium?

View Solution(a) Two point charges Q and 16Q are fixed at separation d. Where should a third point charge be placed between them so that it experiences no force I.e. in equilibrium ?
(b) In the previous problem , if we replace Q by −Q , where should the third charge be placed on the joining the charges so that it is equilibrium ?
(c ) Three point charges Q,q and Q are placed at x=0,x=d/2 and x=d. Find q in terms of Q so that all charges are in equilibrium.
(d) Two point charges 9Q and 25Q are placed at separation d. Where should a third charge q be placed between them so that all charges are in equilibrium ? Also find the value of q and its nature.
View Solution
Knowledge Check
Two points charges +4q and +q are separated by distance r, where should a third point charge Q be placed that the whole system remains in equilibrium
A2r3 from qBr3 from qCr2 from qDr3 from 4qTwo point charges Q and −Q/4 are separated by a distance X. Then
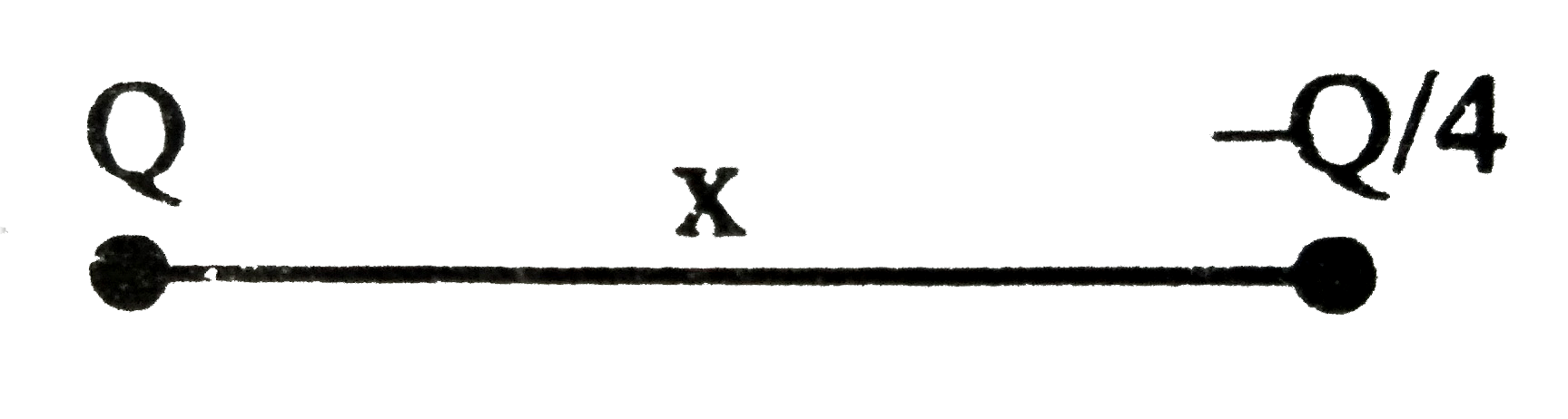 .Apotential is zero at a point on the axis which is x/3 on the right side of the cahrge −q/4Bpotential is zero at a point on the axis which is x/5 on the left side fo the charge −Q/4Celectric field is zero at a point on the axis which is at a distance x on the right side fo the charge −Q/4Dthere exist two points on the axis where electric field is zero.
.Apotential is zero at a point on the axis which is x/3 on the right side of the cahrge −q/4Bpotential is zero at a point on the axis which is x/5 on the left side fo the charge −Q/4Celectric field is zero at a point on the axis which is at a distance x on the right side fo the charge −Q/4Dthere exist two points on the axis where electric field is zero.Two point metal charges−q and +2q are placed at a certain distance apart.Where should a third point charge be placed so that it is in equilibrium?
Aon the line joining the two charges on the right of +2qBon the line joining the two charge on the left of −qCbetween −q and +2qDat any point on the right bisector of the 1 line joining −q and +2q
Two charges Q and -3Q are placed fixed on x-axis separated by a distance 'd' Where should a third charge 2Q be placed such that it will not experience any force?
View SolutionTwo charges q and 3q are placed fixed on x-axis separated by distance 'd'. Where should a third charge 2q be placed such that it will not experience any force ?
View SolutionTwo charge are placed as shown in fig. Where should be a third charge be

View SolutionTwo point charges 2q and 8q are placed at a distance r apart. Where should a third charge −q be placed between them so that the electrical potential energy of the system is a minimum
View SolutionTwo charges +4e and +e are at a distance x apart. At what distance,a charge q must be placed from charge +e so that is in equilibrium
View Solution
