A thin glass rod is bent into a semicircle of radius r. A charge +Q is uniformly distributed along the lower half, as shown in fig. The electric field E at P, the center of the semicircle, is

Qπ2ε0r2
2Qπ2ε0r2
4Qπ2ε0r2
Q4π2ε0r2
The correct Answer is:A
Take PO as the x-axis and PA as the y-axis. Consider two elements EF and E'F' pf width dθ at angular θ above and below PO, respectively

The magnitude of the field at P due to either element is
dE=14πε0rdθ×Q/(πr/2)r2=Q2π2ε0r2dθ
Resolving the field we find that the components along PO sum up to zero, and hence the resultant fields is along PB. Therefore, field at P due to pair of elements is 2dEsinθ
E=∫π/202dEsinθ
=2∫π/20Q2πε0r2sinθdθQπ2ε0r2.
Similar Questions
A wire of length l and charge q is bent in form of a semicircle. The charge is uniformly distributed over the length. The electric field at the centre of semicircle is
View SolutionFigure shows a rod AB, which is bent in a 120∘ circular arc of radius R. A charge (-Q) is uniformly distributed over rod AB. What is the electric field →E at the centre of curvature O ?
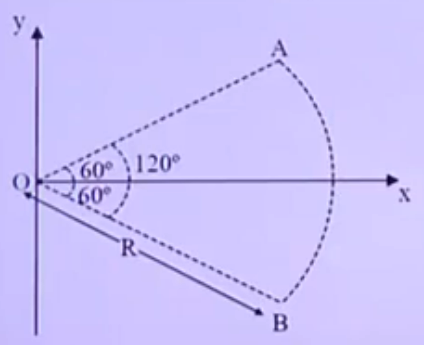
View Solution
Knowledge Check
Charges q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
Aq2π2ε0R2Bq4π2ε0R2Cq4πε0R2Dq2πε0R2semicircle of radius R. The electric field at the centre is -
A2kλRBkλ2RCZeroDNoneA thin semi-circular ring of radius r has a positive charge q distributed uniformly over it as shown in the figure. The net field →E at the center O is
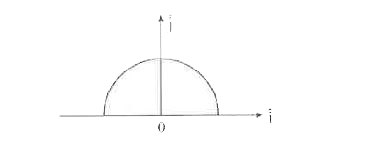 Aq2π2ε0r2ˆjBq4π2ε0r2ˆjC−q2π2ε0r2ˆjD−q2π2ε0r2ˆj
Aq2π2ε0r2ˆjBq4π2ε0r2ˆjC−q2π2ε0r2ˆjD−q2π2ε0r2ˆj
A non-conducting wire is bent into a semi-circle of radius R and a charge +Q is uniformly distributed over it as shown in the figure. Find the ratio (VAEA) of the potential (VA) to the magnitude of the electric field (EA), both evaluated at the other end A of diameter AB that bisects the wire (as shown in the figure)
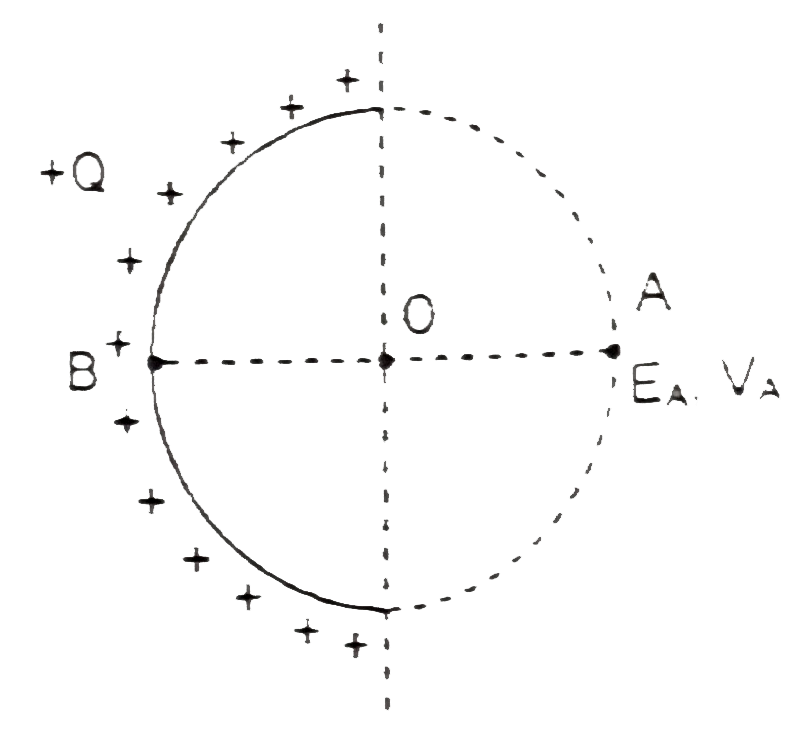
View SolutionA positive charge Q is uniformly distributed along the length L of a rod. It is bent in the shape of a square. Calculate electric field intensity at the centre of the square.
View SolutionA wire of length L carries charge Q uniformly distributed along its length. Find the electric field at a distance √3L2 from the wire at point A as shown.
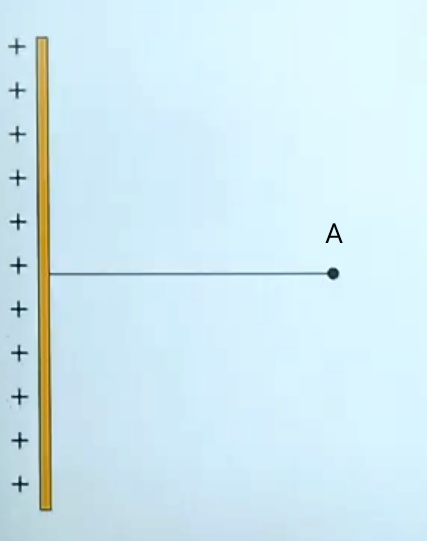
View SolutionA spherical shell of radius R has a uniformly distributed charge ,then electric field varies as
View SolutionA charge −Q is unformly distributed over a non-conducting semi-circular rod of radius R. The potential at the center is
View Solution
