Gauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
The net flux of the electric field through the surface due to q3 and q4 is
zero
positive
negative
cannot say
The correct Answer is:A
To solve the problem of finding the net electric flux through a Gaussian surface due to charges q3 and q4, we can follow these steps:
Step 1: Understand Gauss's Law
Gauss's Law states that the electric flux ΦE through a closed surface is proportional to the charge enclosed qencl within that surface. Mathematically, it is given by:
ΦE=qenclϵ0
where ϵ0 is the permittivity of free space.
Step 2: Identify the Charges
Assume we have two point charges q3 and q4. We need to determine whether these charges are inside or outside the Gaussian surface we are considering.
Step 3: Calculate the Enclosed Charge
If both charges q3 and q4 are inside the Gaussian surface, then the total enclosed charge qencl is:
qencl=q3+q4
If one or both charges are outside the surface, then they do not contribute to the enclosed charge, and we only sum the charges that are inside.
Step 4: Apply Gauss's Law
Using Gauss's Law, we can now calculate the electric flux through the surface:
ΦE=qenclϵ0
Step 5: Substitute Values
If we know the values of q3 and q4, we can substitute them into the equation to find the net electric flux.
Example Calculation
Assuming q3=+2μC and q4=−3μC:
1. Calculate the enclosed charge:
qencl=2μC−3μC=−1μC
2. Calculate the electric flux:
ΦE=−1×10−68.85×10−12≈−113,000N m2/C
Final Result
The net electric flux through the Gaussian surface due to charges q3 and q4 is approximately −113,000N m2/C.
---
Gauss's Law states that the electric flux ΦE through a closed surface is proportional to the charge enclosed qencl within that surface. Mathematically, it is given by:
Assume we have two point charges q3 and q4. We need to determine whether these charges are inside or outside the Gaussian surface we are considering.
If both charges q3 and q4 are inside the Gaussian surface, then the total enclosed charge qencl is:
Using Gauss's Law, we can now calculate the electric flux through the surface:
If we know the values of q3 and q4, we can substitute them into the equation to find the net electric flux.
Assuming q3=+2μC and q4=−3μC:
qencl=2μC−3μC=−1μC
ΦE=−1×10−68.85×10−12≈−113,000N m2/C
The net electric flux through the Gaussian surface due to charges q3 and q4 is approximately −113,000N m2/C.
Similar Questions
Knowledge Check
Gauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
A Gaussian surface encloses two of the four positively charged particles. The particles that contribute to the electric field at a point P on the surface are
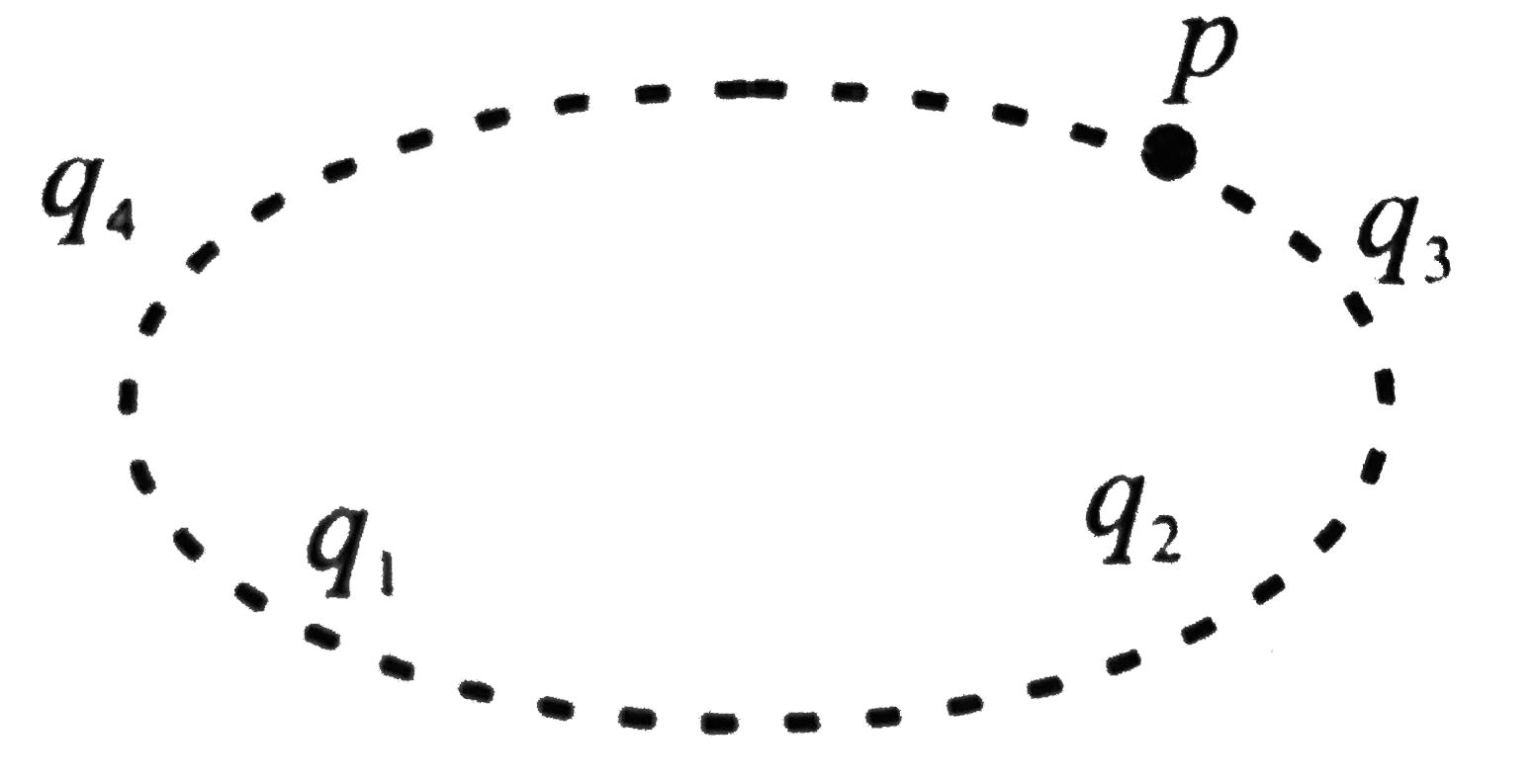 Aq1 and q2Bq2 and q3Cq4 and q3Dq1,q2,q3 and q4
Aq1 and q2Bq2 and q3Cq4 and q3Dq1,q2,q3 and q4Gauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
If the charge q3 and q4 are displaced (always remaining outside the Gaussian surface), then consider the following two statements :
A: Electric field at each point on the Gaussian surface will remain same .
B: The value of ∮→E.d→A for the Gaussian surface will remain same.ABoth A and B are true .BBoth A and B are false.CA is true , but b is false.DB is true , but A is false.In Gauss' s theorem ∮sEds=qε0 The surface integral is evaluated by choosing a closed surface called the Gaussian surface. Here
AThe closed surface can be of any shape or size.Bq is the net charge enclosed inside the Gaussian surface, charges outside the surface are not considered.CE is the electric field due to all the charges both inside and outside the surface.DThe exact location of the charges inside the surface does not affect the value of the integral.
A charge Q is enclosed by a Gaussian surface. If surface area is doubled and charge Q is tripled then the outward electric flux will
View SolutionA point charges of 2.0μC is at the centre of a cubic Gaussian surface 9.0cm on edge . What is the net electric flux through the surface?
View SolutionThe surface considered for Gauss's law is called
View SolutionA charge q is inside a closed surface and charge -q is outside. The out going electric flux is
View SolutionA point charge 4μC is at the centre of a cubic Gaussian surface 10 cm on edge. Net electric flux through the surface is
View Solution
