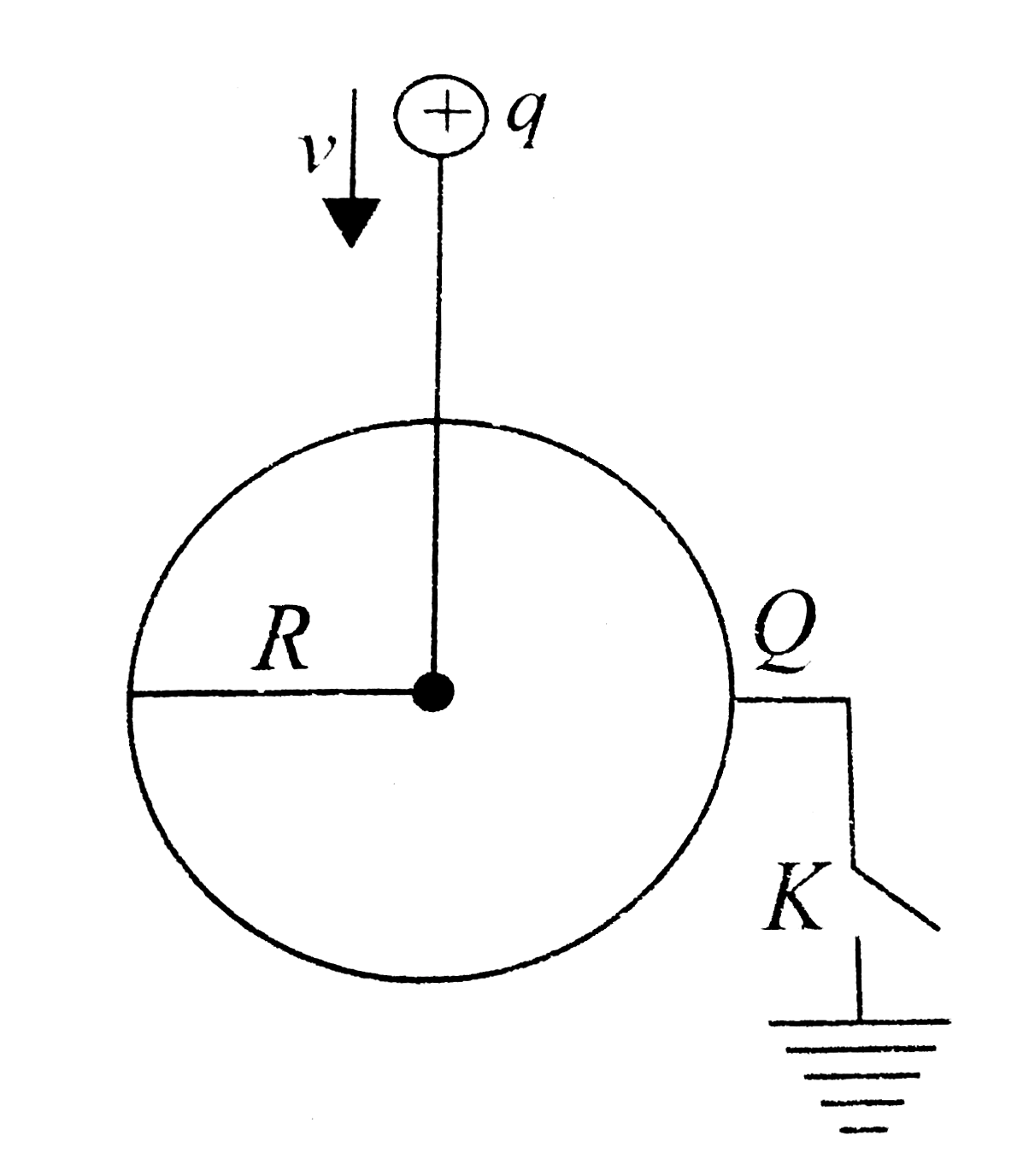
A point charge +q is moved with a constant velocity v toward a solid conducting sphere carrying a charge Q. Find the (a) potential of the sphere, (b) charge induced as the function of r, (c ) charge flowing if we close the key K, and (d) current is the part (c ).
Video Solution
Text Solution
a. We find potential at the center of sphere.
V=kqr+kQR=14πε0[qr+QR]
b. If key is closed, potential of sphere should be zero.
V=0ork(qr+QR)=0orQ=−qRr
c. Charge flowing through key is q'=qRr
d. I=dqdt=dR−r2drdt=dR−r2(−v)=qRvr2
|
Similar Questions
Knowledge Check
A point charge q is placed at a distance of r from cebtre of an uncharged conducting sphere of rad R(<r). The potential at any point on the sphere is
AzeroB14πε0qrC14πε0qRr2D14πε0qr2RA conducting sphere of radius R and carrying a charge Q is joined to an uncharged conducting sphere of radius 2R. The charge flowing between them will be
AQ/4BQ/3CQ/2D2Q/3A conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the centre of the sphere respectively are
AZero and Q4πε0R2BQ4πε0R2 and zeroCQ4πε0R and Q4πε0R2DBoth are zero
A conducting sphere of radius 2R carrying charge Q is joined to an uncharged conducting sphere of radius R. Find the charge flow through cinnecting wire.
View SolutionAn isolated solid metallic sphere is given +Q charge. The charge will be distributed on the sphere
View SolutionA solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :

View SolutionA metal sphere of radius r is charged to certain potential V. Then the charge on the metal sphere
View SolutionMetallic sphere of radius R is charged to potential V. Then charge q is proportional to
View Solution
