An 80μC charge is given to the 4μF capacitor in the circuit shown in Fig. so the upper plate A is positively charged. An unknown resistance R is connected in the left limb. As soon as the switch S in the central limb is closed, a current of 2 A flows through the 2Ω resistor in the central limb. The capacitive time constant for the circuit is

56μs
8μs
200μs
40μs
The correct Answer is:D
d. Potential difference across the central limb = 16 V = Potential difference across 16Ω = potential across the left
limb.
Current through 16Ω = 1A
Current through the left limb = 1 A and R = 11Ω
∴τC=(162+2)Ω×(4×10−6)F=40μs .
Similar Questions
दिए गए परिपथ में 4μF धारिता के संधारित्र पर आवेश का मान होगा
View Solutionदिये गये परिपथ में 4μF के संधारित्र की ऊपरी प्लेट पर +80μC आवेश दिया जाता है| तब स्थिर अवस्था में, 3μF संधारित्र की ऊपरी प्लेट पर आवेश होगा|
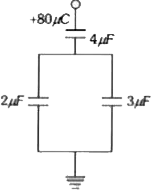
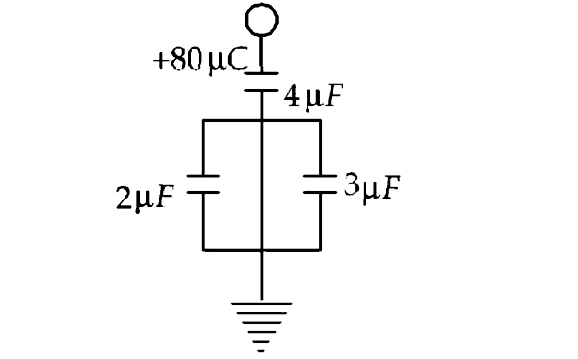
View SolutionIn the given circuit, a charge of +80μC is given to the upper plate of the 4μF capacitor. Then in the steady state, the charge on the upper plate of the 3μF capacitor is
View SolutionIn the circuit shown in fig. when the switch is closed, the capacitor charges with a time constant
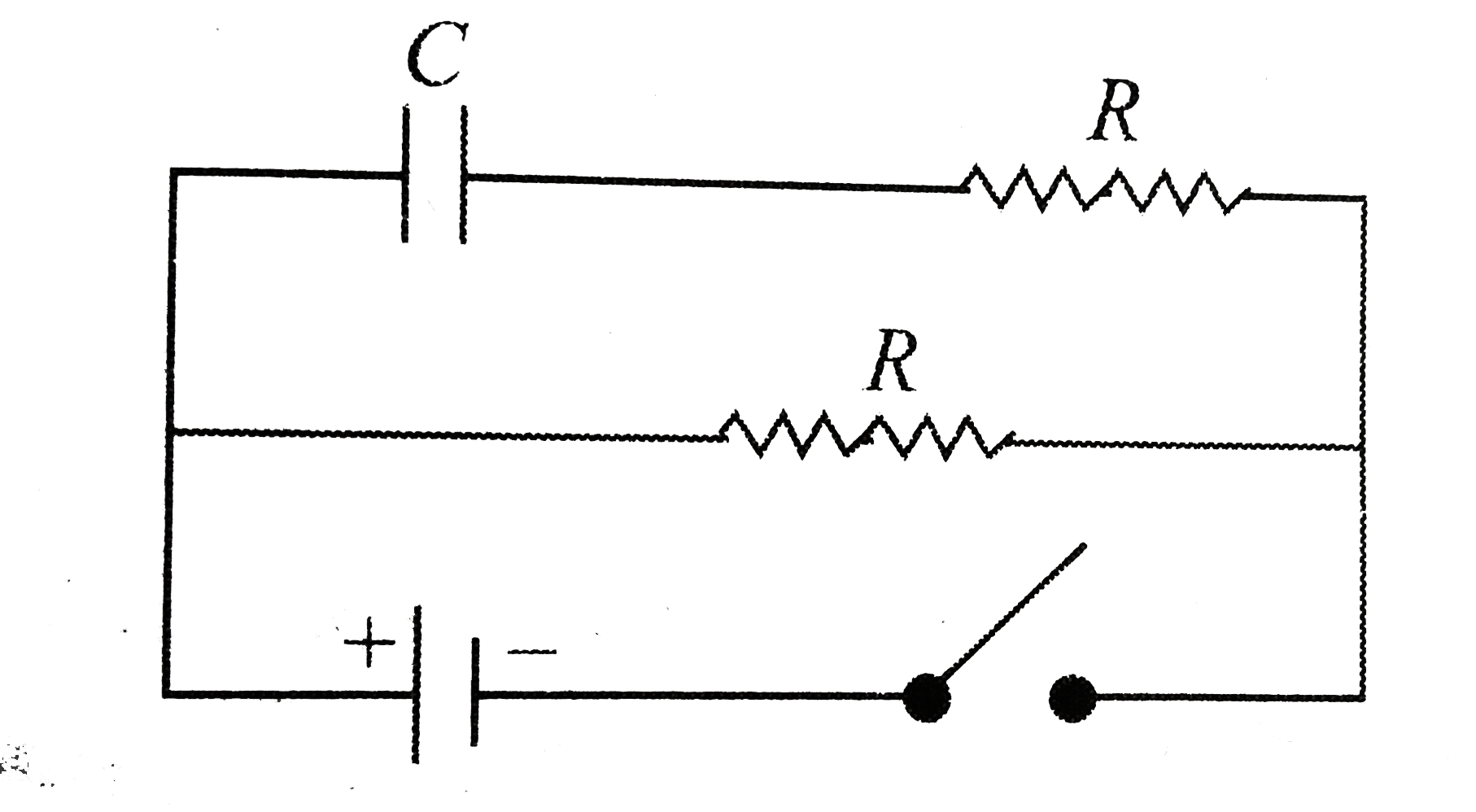
View SolutionAn 80μC charge is given to the 4μF capacitor in the circuit shown in Fig. so thae upper plate A is positively charged. An unknown resistance R is connected in the left limb. As soon as the switch S in the central limb is closed, a current of 2 A flows through the 2Ω resistor in the central limb. The capa citive time constant for the circuit is

View SolutionIn the circuit shown in fig, if the switch S is closed at t=0 , the capacitor charges with a time constant

View SolutionThree capacitors (of capacitances C , 2C and 3C ) and three resistors (of resistance R , 2R and 3R ) are connected with a battery and switch S as shown in the figure. When switch S is open, charges on the capacitors are shown. Switch S is closed at t=0 sec . The time constant of the circuit will be
View SolutionA capacitor of 4muF is connected as shown in the circuit. The internal resistance of the battery is 0.5 Omega . The amount of charge on the capacitor plates will be
View Solution

