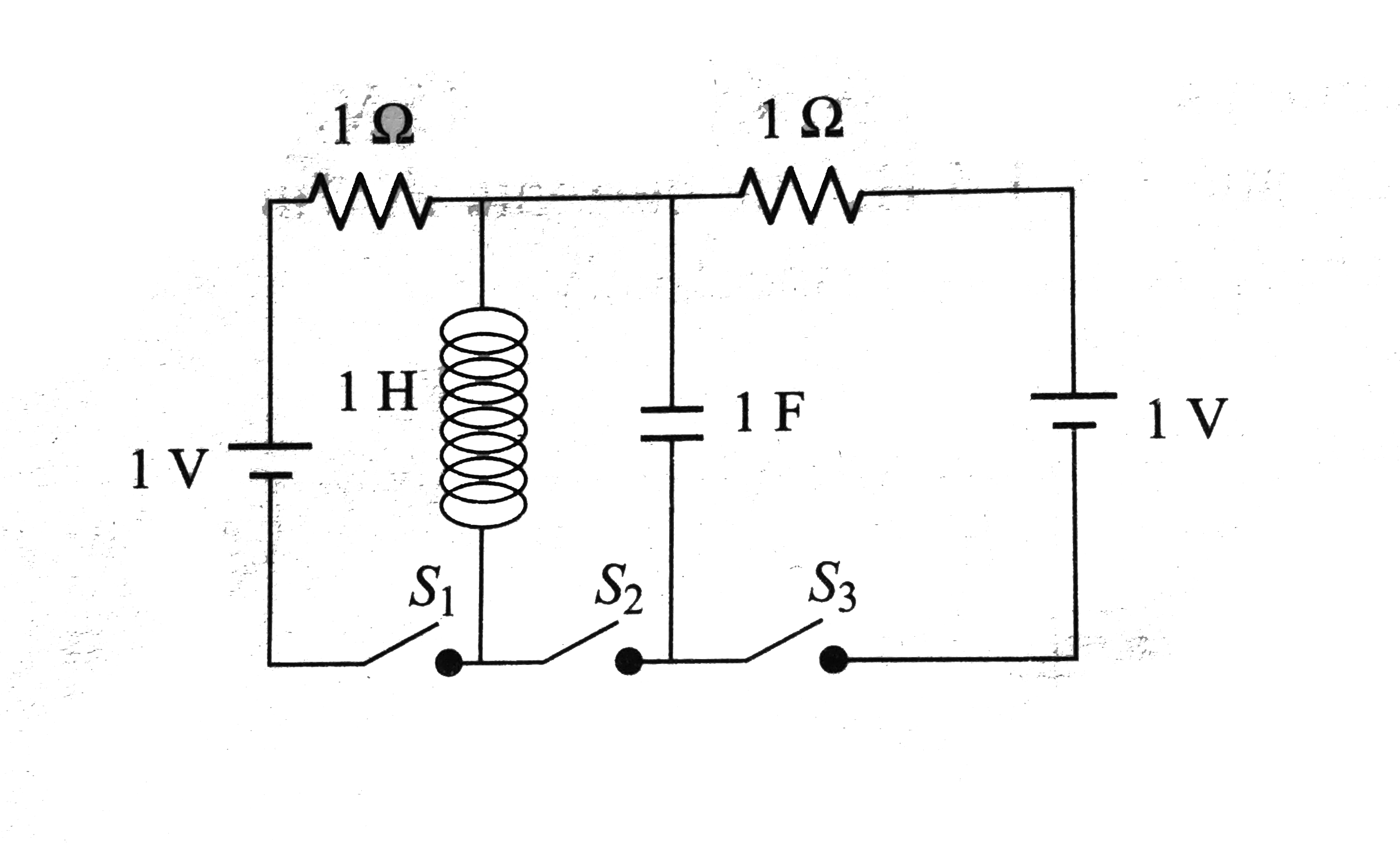
In the circuit shows (Fig.) switches S1 and S3 have been closed for 1s and S2 remained open. Just after 1s, switch S2 is closed and S1 and S3 are opened. Find after that instant (t=0):
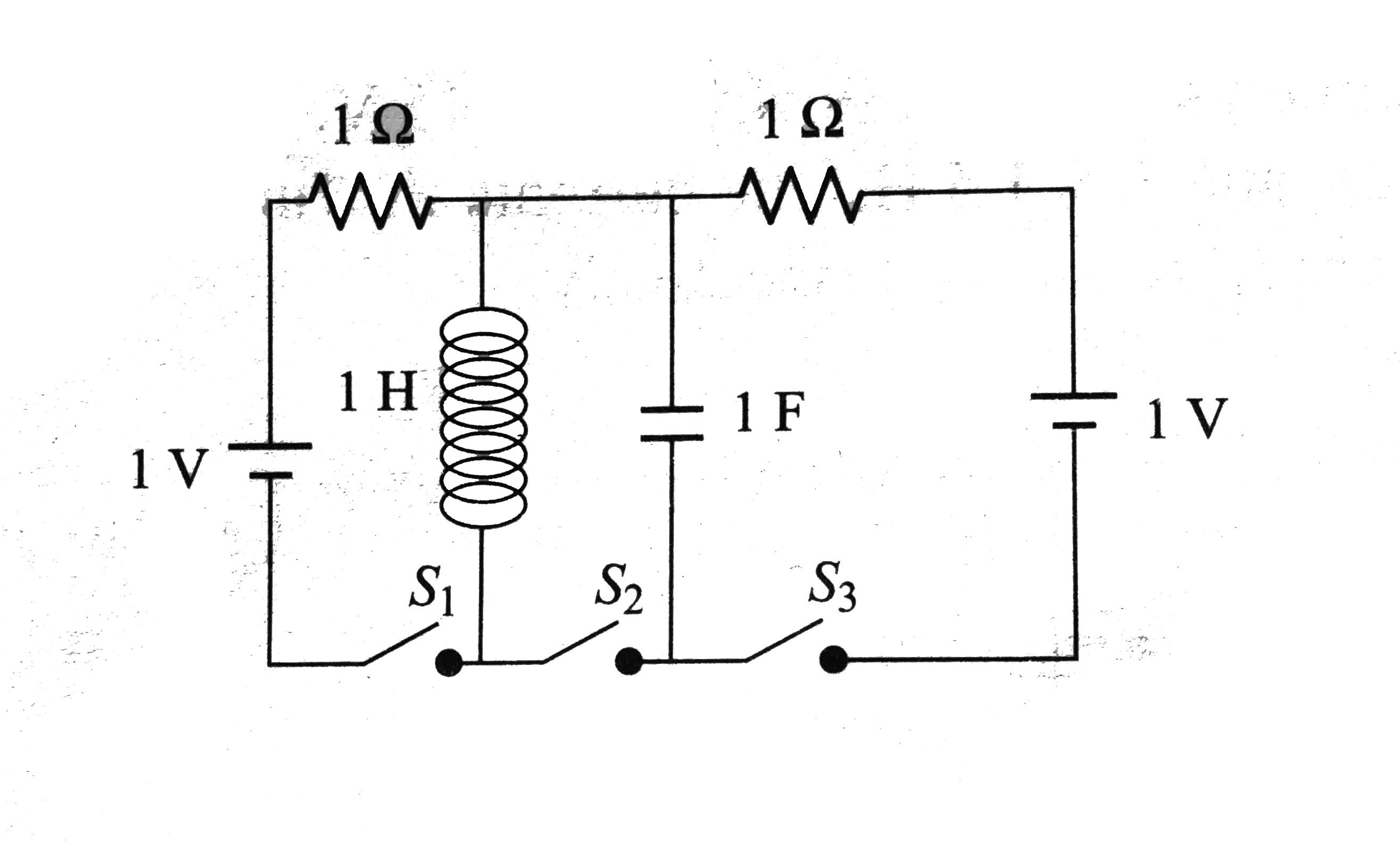
the charge on the upper plate of the capacitor as a funtion of time
√2(1−1e)sin(t+3π4)
√2(1−1e)sin(t+π4)
√3(1−1e)sin(t+π4)
√3(1+1e)sin(t+π4)
The correct Answer is:A
S1 and S2 are closed for 1s.
Charge on capacitor,
q=CE(1−e−t/RC)=1−1e (i)
The current in inductor,
I=ER(1−e−t/RC)=1−1e(ii)
Now S1 and S3 are opened and S2 is closed,
It is LC circuit,
q=qmaxsin(ωt+ϕ) (iii)
I=(qmax)ωcos(ωt+ϕ) (iv)
As total energy (Magnetic + electrical) is constant
12LI2max=12q2maxC=12LI2+12q2C (v)
qmax=√2(1−1e) (vi)
Imax=√2(1−1e) (vii)
From (iii) at t=0, we get
(1−1e)=√2(1−1e)sinϕ⇒=π4 or 3π4
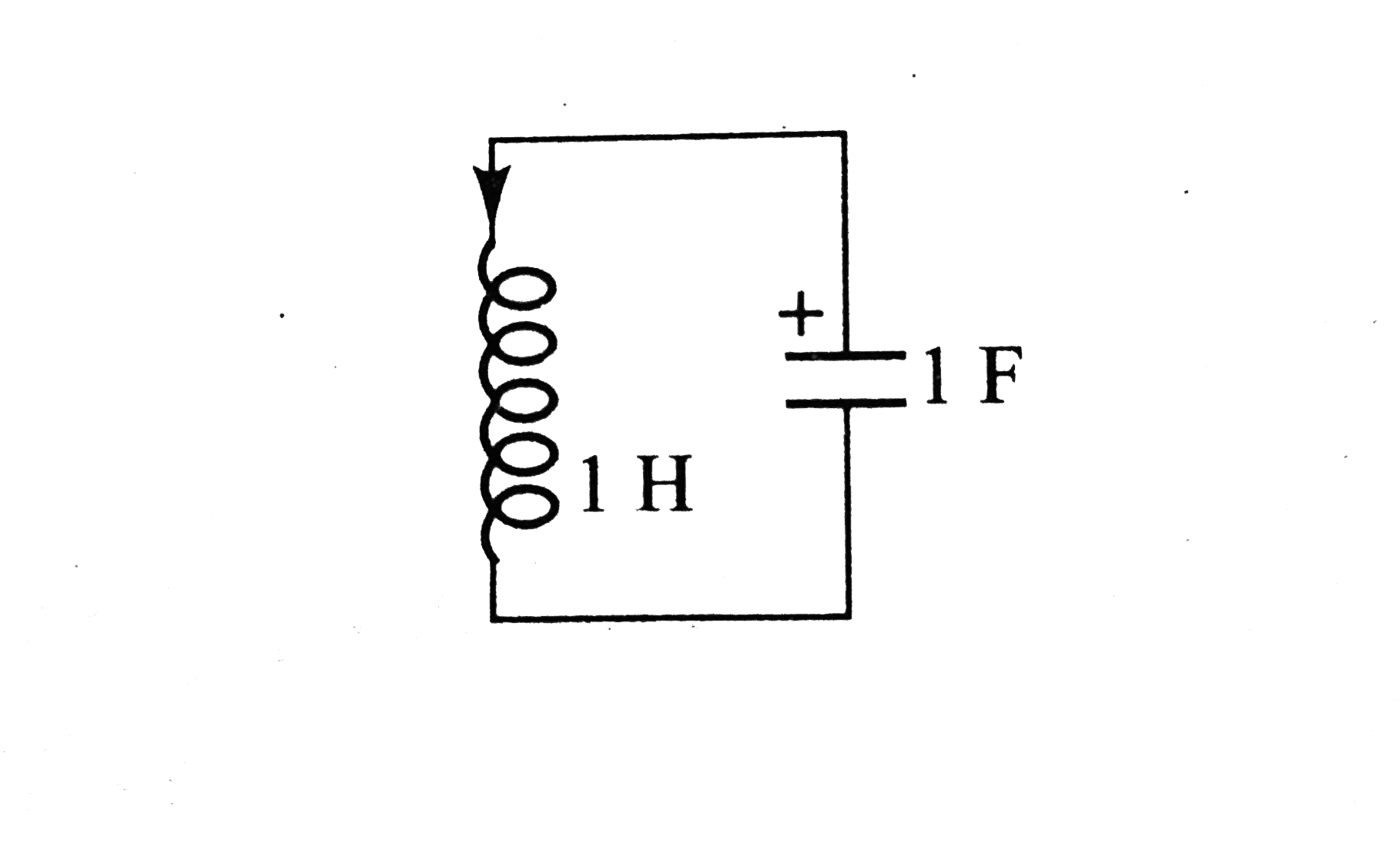
After closing S2, circuit will be as shows. Direction of current shows that charge on capacitor will be decreaseing. Hence ϕ=3π/4
q=√2(1−1e)sin(ωt+3π4)
where, ω=1√LC=1
q=√2(1−1e)sin(t+3π4)
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (integer)
8 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Archives (fills In The Blanks)
3 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (assertion-reasoning)
2 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
28 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
Similar Questions
Figure shows a part of a bigger circuit. The capacity of the capacitor is 6mF and is desaesing at the constate rate 0.5mFs−1. The potential difference across the capacitor at the shows moment is changing as follows:
dVdt=2Vs−1, d2Vdt2=12VS−2
The current in the 4Ω resistor is decreasing at the rate of 1mAs−1. What is the potential difference (in mV) across the inductor at this moment?

View SolutionA uniform wound solenoidal coil of self inductance 1.8×10−4 henry and resistance 6 ohm is broken up into two identical coils. These identical coils are then connected in parallel across a 15-volt battery of negligible resistance. The time constant for the current in the circuit is.......seconds and the steady state current through the battery is ..............amperes.
View SolutionStatement I: Two coaxial conducting rings of different radii are placed in space. The mutual inductance of both the rings is maximum if the rings are also copanar.
Statement II: For two coaxical conducting rings of different radii, the magitude of magnetic flux in one ring due to current in the other ring is maximum when both the rings are copanar.
View SolutionA room AC run for 5 hour at a voltage of 220V The wiring of the room constant of Cu of 1mm ratio and a length of 10m consumption per day is 10 commerclal unit What fraction of it goes in the joule heated in wire? What would happen if the wiring is made of aluminum of the same distances? [ρcu=1.7×10−8Ω,ρA1=2.7×10−8Ωm]
View SolutionAir is filled at 60 ∘ C in a vessel of open mouth. The vessel is heated to a temperature T so that 14 part of air escapes. The value of T(in 0C) is
View SolutionIn the circuit shows (Fig.) switches S1 and S3 have been closed for 1s and S2 remained open. Just after 1s, switch S2 is closed and S1 and S3 are opened. Find after that instant (t=0):
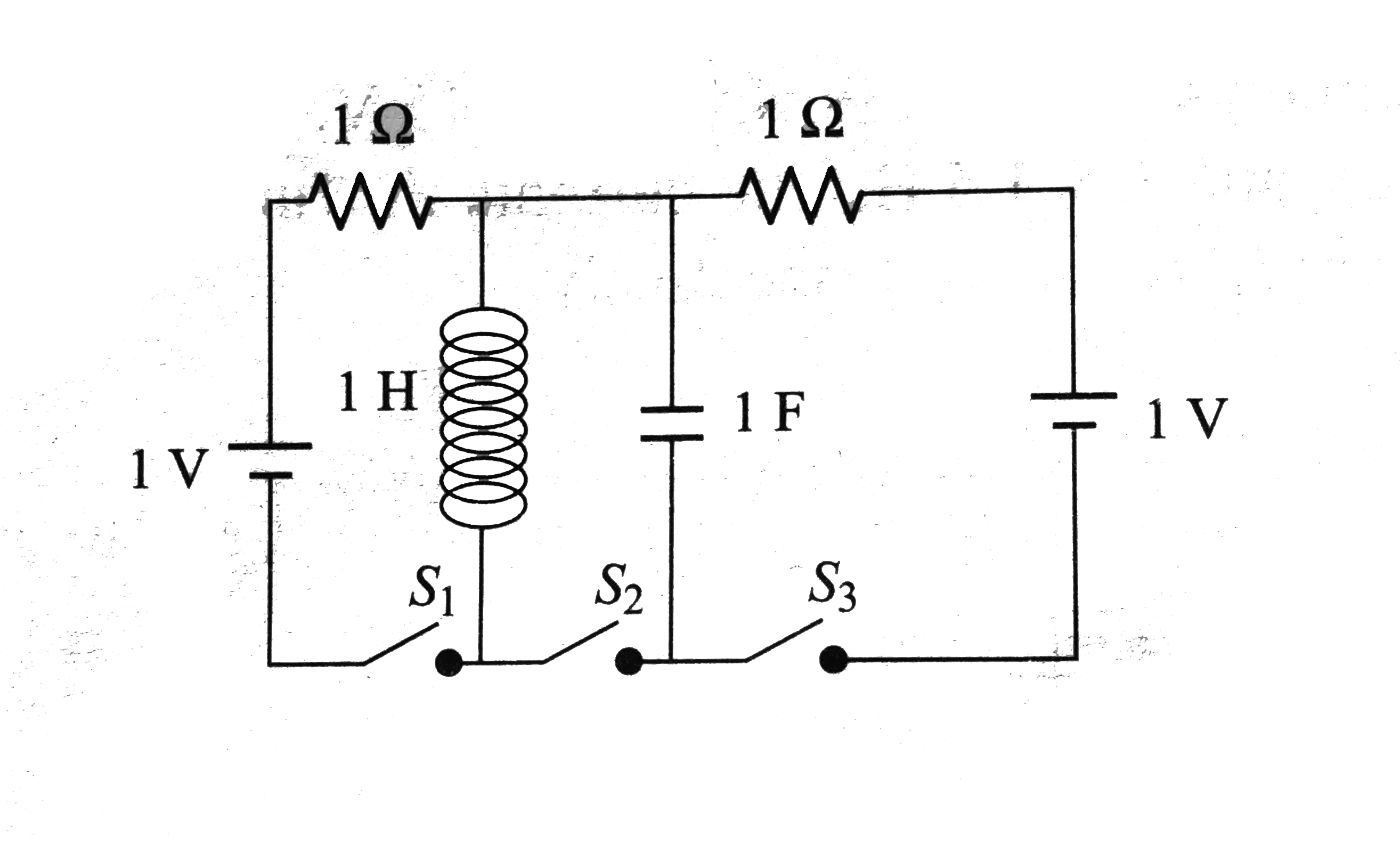
the maximum current in the circuit containing inductor and capacitor (only S2 is closed)
View SolutionIn the circuit shows (Fig.) switches S_(1) and S_(3) have been closed for 1 s and S_(2) remained open. Just after 1 s , switch S_(2) is closed and S_(1) and S_(3) are opened. Find after that instant (t = 0) : the maximum charge on the capacitor
View SolutionIn the circuit shown, the capacitor is initially charged with a 12V battery, when switch S1 is open and switch S2 is closed. S1 is then closed and, at the same time, S2 is opened. The maximum value of current in the circuit is
View SolutionIn the circuit shown switches S_(1) and S_(2) have been closed for 1 sec and S_(2) remained open.Just after 1 second is over switch S_(2) is closed and S_(1),S_(3) are opened.Find after that instant The charge on the upper plate of the capacitor as function of time taking the instant of switching on of S_(2) and switching off all time switches to be t=0 is q=x xx10^(-2)cos (t+pi/4) .Findout value of x .
View SolutionAs shown in diagram initial charge on capacitor is zreo . Now switch S_(1) is closed & it remains closed for a long time but S_(2) remains open . Now switch S_(1) is opened & switch S_(2) is closed at t=0, then after closing the switch S_(2) :
View SolutionIn the circuit given below, the capacitor C is charged by closing the switch S1 and opening the switch S2. After charging, the switch S1 is opened and S2, is closed, then the maximum current in the circuit

View SolutionIn the circuits shows in S1 and S2 are switches. S2 remains closed for a long time and S1 is opened. Now S1 is also closed. Just after S1 is closed, find the potential difference (V) across R and di/dt (with sign) in L.

View SolutionIn the circuit shows (Fig.) switches S1 and S3 have been closed for 1s and S2 remained open. Just after 1s, switch S2 is closed and S1 and S3 are opened. Find after that instant (t=0):

the maximum current in the circuit containing inductor and capacitor (only S2 is closed)
View SolutionIn the circuit shows (Fig.) switches S1 and S3 have been closed for 1s and S2 remained open. Just after 1s, switch S2 is closed and S1 and S3 are opened. Find after that instant (t=0):
the maximum charge on the capacitor
View SolutionIn the circuit shows (Fig.) switches S_(1) and S_(3) have been closed for 1 s and S_(2) remained open. Just after 1 s , switch S_(2) is closed and S_(1) and S_(3) are opened. Find after that instant (t = 0) : the charge on the upper plate of the capacitor as a funtion of time
View Solution

