In problem 9 the acceleration of the particle is
A
10πm and 5πms2
B
5πm and 5π2ms2
C
10πm and 5π2ms2
D
5πm and 5π4ms2
Video Solution
Text Solution
The correct Answer is:C
From the graph T=(5−1)=4s
(distance between the two adjacent shown in the figure)
and vmax=5ms,ωA=5ms
(2πT)A=5⇒A=5T2π=5×42π=10π m
Also ω=2π4=π2rads
The equation of velocity can be written as
v=5sin(π2)tms
At extreme position, v=0, sin(π2)t=0 or t=2s
Phase of the particle velocity at that insstant corresponding to the above equation =π
Therefore, when a phase change of π5 takes place, the resulting phase=π+π6
v=5sin(π+(π)6)=−5sin(π6)=−5(12)
=2.5ms (numerically)
dydt=v⇒dy=dt
dy=∫5sin(πt2)dt=10π[−cos(πt2)]+C
Since at t=0, the particle is at the extreme position, there fore at r=0,y=−10π
−10π=−10πcosθ+C⇒C=0
y=−10πcos(πt2)
Clearly a phase change of π6 corresponds to a time difference of T2π(π6)=T12=412=13s
y=−10πcos(π6)=−10π(√32)
=5√3πm (numerically)
Acceleration a=dvdt=ddt(5sin(πt2))=5π2cosπt2
a at t=13s=5π2cos(π6)=5π√34ms2
Maximum displacement xmax=A=10πm
and maximum accceleration, amax=ω2A
=(π2)2×10π=5π2ms2
|
Similar Questions
Knowledge Check
A particle revolves round a circular path with a constant speed the acceleration of the particle is :
Aalong the circumference of the circleBalong the tangentCalong the radiusDzeroTwo particles of equal mass have velocities and . First particle has an acceleration while the acceleration of the other particle is zero. The centre of mass of the two particles moves in a path of
Astraight lineBparabolaCcircleDellipseWhen a force F acts on a particle of mass m, the acceleration of particle becomes a. now if two forces of magnitude 3F and 4F acts on the particle simultaneously as shown in figure, then the acceleration of the particle is
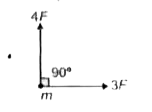 AaB2aC5aD8a
AaB2aC5aD8a
For a particle revolving in a circular path, the acceleration of the particle is
View SolutionA particle revolves round a circular path. The acceleration of the particle is inversely proportional to-
View SolutionA particle is moving in a circle with a constant speed, the acceleration of the particle has
View SolutionA particle revolves round a circular path. The acceleration of the particle is inversely proportional
View SolutionThe velocity -time (v−t) graph of a particle moving in a straight line is shown in figure. The acceleration of the particle at t=9 is:
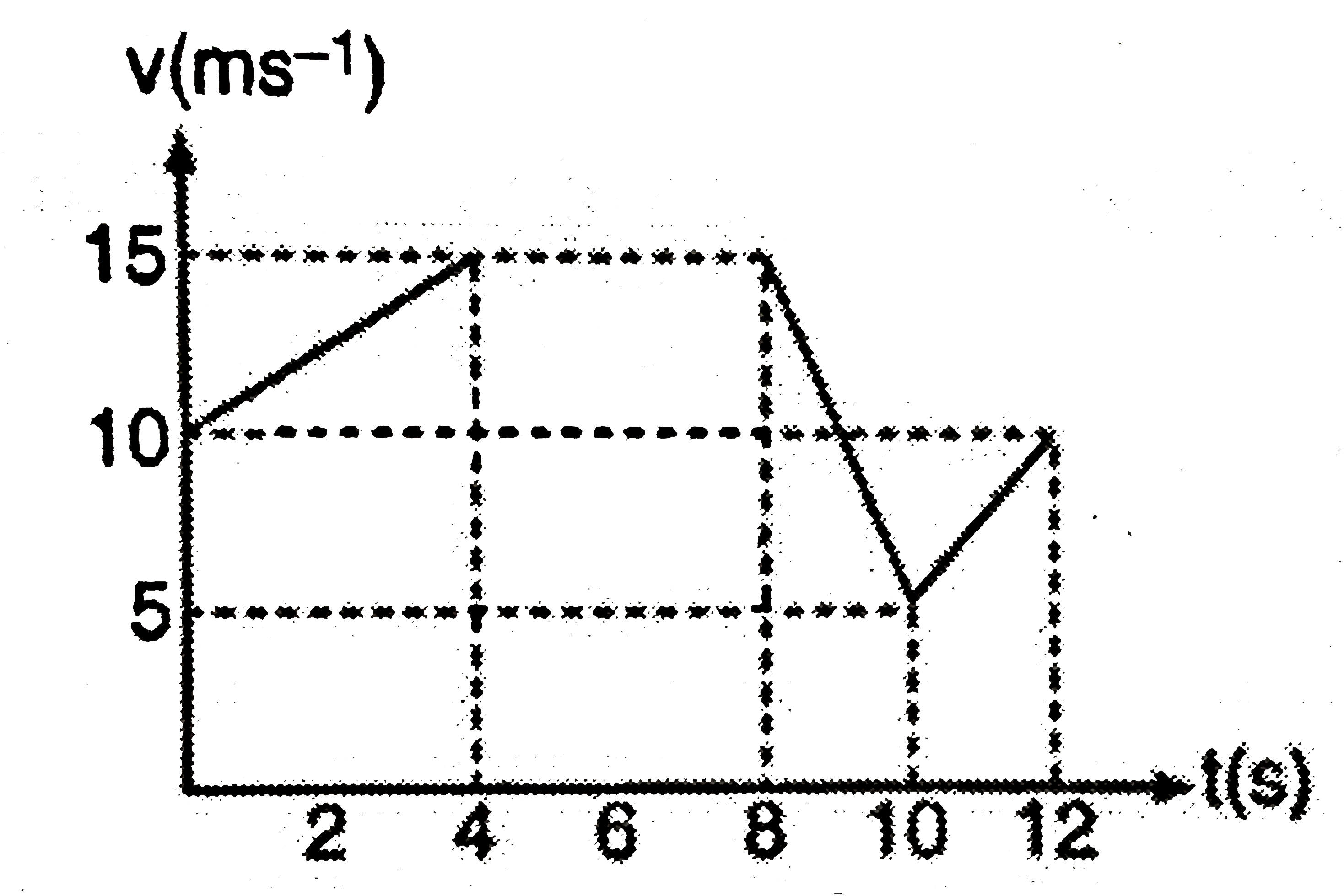
View Solution