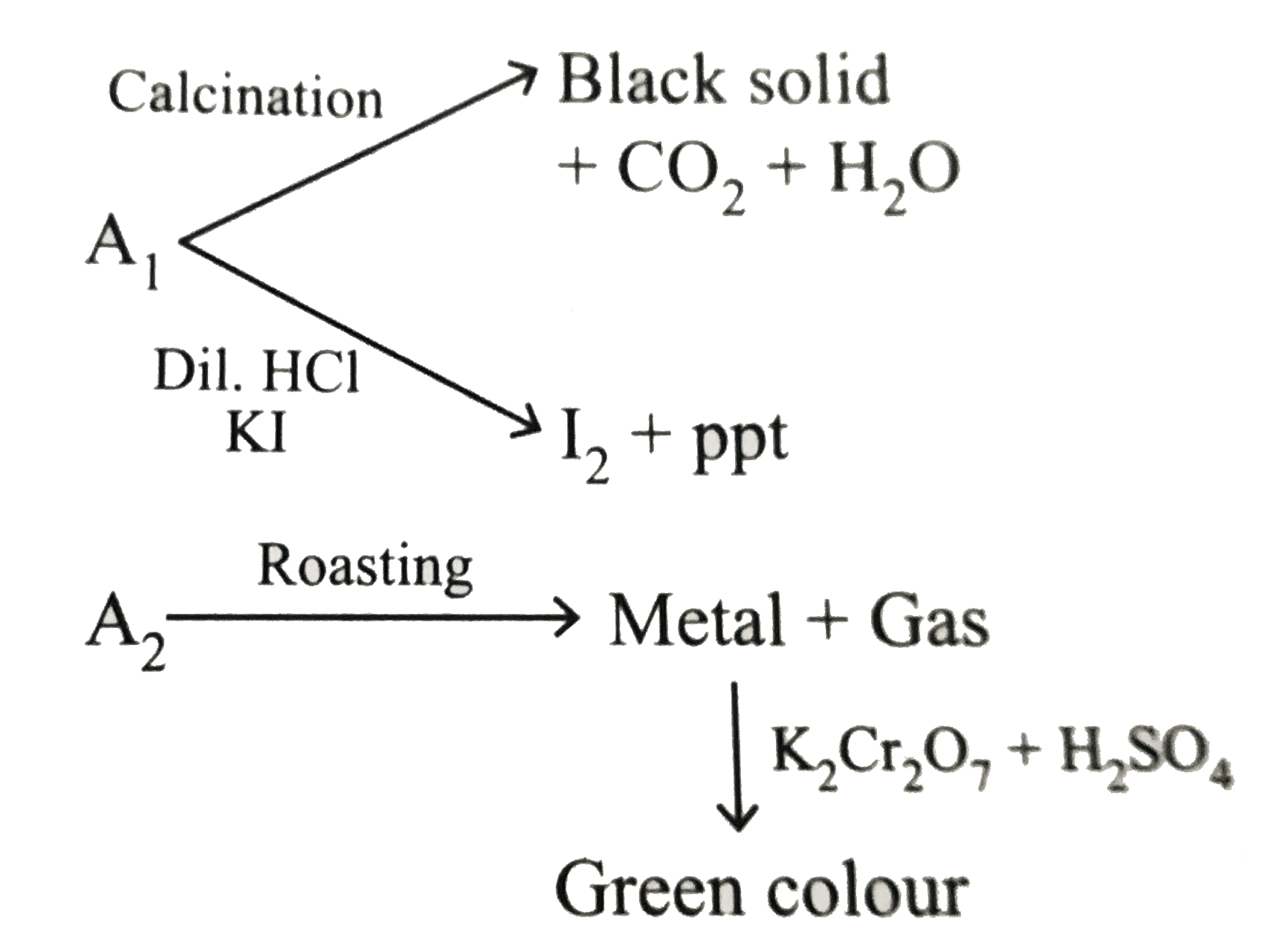
A1 and A2 are two ores of metal M.A1 on calcination gives black precipitate, CO2 and water. Identify A1 and A2.
A1 is malachite CuCO3.Cu(OH)3
CuCO3Cu(OH)2Δ−−→CuO+CO2↑⏐⏐+H2O
CuO is the black solid.
CuCO3.Cu(OH)2dil.HCl−−−−→CuCl2+CO2+H2O
CuCl2KI−−→Cu2I2+KCl+I2
A2 is copper glance Cu2S, a sulphide ore.
Cu2SO2−−→ΔCu2O+SO2
Cu2S+Cu2O→Cu+SO2
The gas SO2 gives green colour with acidified K2Cr2O7.K2Cr2O7+H2SO4+3SO4→K2SO4+Cr2(SO4)3+4H2O
Similar Questions
Knowledge Check
If A1B2 and A2B2 are two focal chords of the parabola y2=4ax then the chords A1A2 and B1B2 intersect on
AdirectrixBaxisCT.V.DnoneTwo AMs.A1 and A2, two GMs. G1 and G2 and two HMs. H1 and H2 are inserted between any two numbers. Then find the arithmetic mean between H1 and H2 in terms of A1,A2,G1,G2.
AA1+A22G1G2BA1−A22G1G2CA1+A22+G1G2DG1+G22A1A2A statue built on a 50 m high pedestal subtends 45∘ at two points, A1 and A2,50 m apart on the ground. If the straight line joining A1andA2 passes through the base of the pedestal, then what is the height of the statue (without the pedestal) (assume that the statue and pedestal are vertical)
A25√2B50C150D250
If the number of sides of two regular polygons having the same prerimeter be nand2n respectiely, prove that their areas are in the ratio 2cosπn:(1+cosπn)
View SolutionIfx,y,z are in A.P. andA1is the arithmetic mean of x,y and A2is the arithmetic mean of y,z then prove that the arithmetic mean of A1and A2isy
View SolutionThe equation Ax−a1+A2x−a2+A3x−a3=0whereA1,A2,A3>0anda1<a2<a3 has two real roots lying in the invervals. (A) (a1,a2)and(a2,a3) (B) (−∞,a1)and(a3,∞) (C) (A1,A3)and(A2,A3) (D) none of these
View SolutionThe distributive law from algebra states that for all real numbers c,a1 and a2,we have c(a1+a2)=ca1+ca2 Use this law and mathematical induction to prove that,for all natural numbers,n≥2,if c,a1,a2,....,an are any real numbers,then c(a1+a2+.....+an)=ca1+ca2+....+can
View SolutionIn the following circuit readings in ammeters A1 and A2 will be -

View Solution


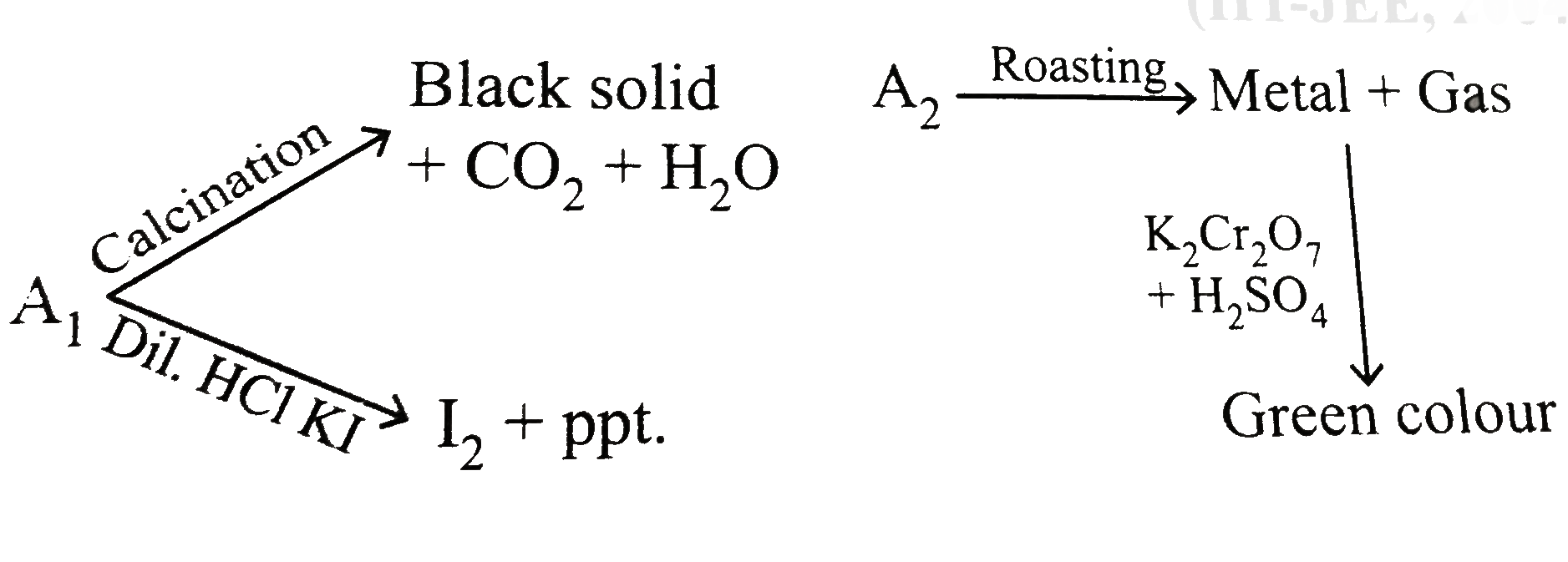 .
.