Weight mg of a block is a force acting downward toward centre of the earth. A block of mass 1kg is placed on an inclined plane as shown in figure. Find the x-component and y-component of weight of the block are

6N,−8N
6N,8N
8N,6N
8N,−6N
The correct Answer is:A

mg=1×10=10N
From figure, the x-component is
mgsin37∘=1×10×35=6N
and y-component is
−mgcos37∘=−1×10×45=−8N
Similar Questions
एक खुरदरे क्षैतिज तल पर रखे 1.5 किग्रा द्रव्यमान के एक गुटके को 1.2 किग्रा-भार के क्षैतिज बल से खींचा जाता है। तल तथा गुटके के बीच घर्षण गुणांक 0.3 है। गुटके में उत्पन्न त्वरण का मान g के पद में ज्ञात कीजिए।
View SolutionWhen a block is kept on the table, its weight acts vertically downwards then the force exerted by the surface on the block is
View SolutionA 10 kg block kept on an inclined plane is pulled by a string applying 200 N force. A 10 N force is also applied on 10 kg block as shown in figure. Find : acceleration of 10 kg block.
View Solution[" A block of mass "m" is placed over "],[" rough inclined plane having "],[" inclination "30^(@)." The co-efficient of "],[" friction between the block and "],[" inclined plane is "0.75" .The contact "],[" force on the block is "(x)/(4)mg" .Find the "],[" value of "x]
View SolutionA block of mass m is placed over rough inclined plane having inclination 30^(@) .The co-efficient of friction between the block and inclined plane is 0.75.The contact force on the block is x/4mg . Find the value of x
View SolutionA block of mass 1 kg is placed on a horizontal surface . The reaction force to the weight of the block is
View Solution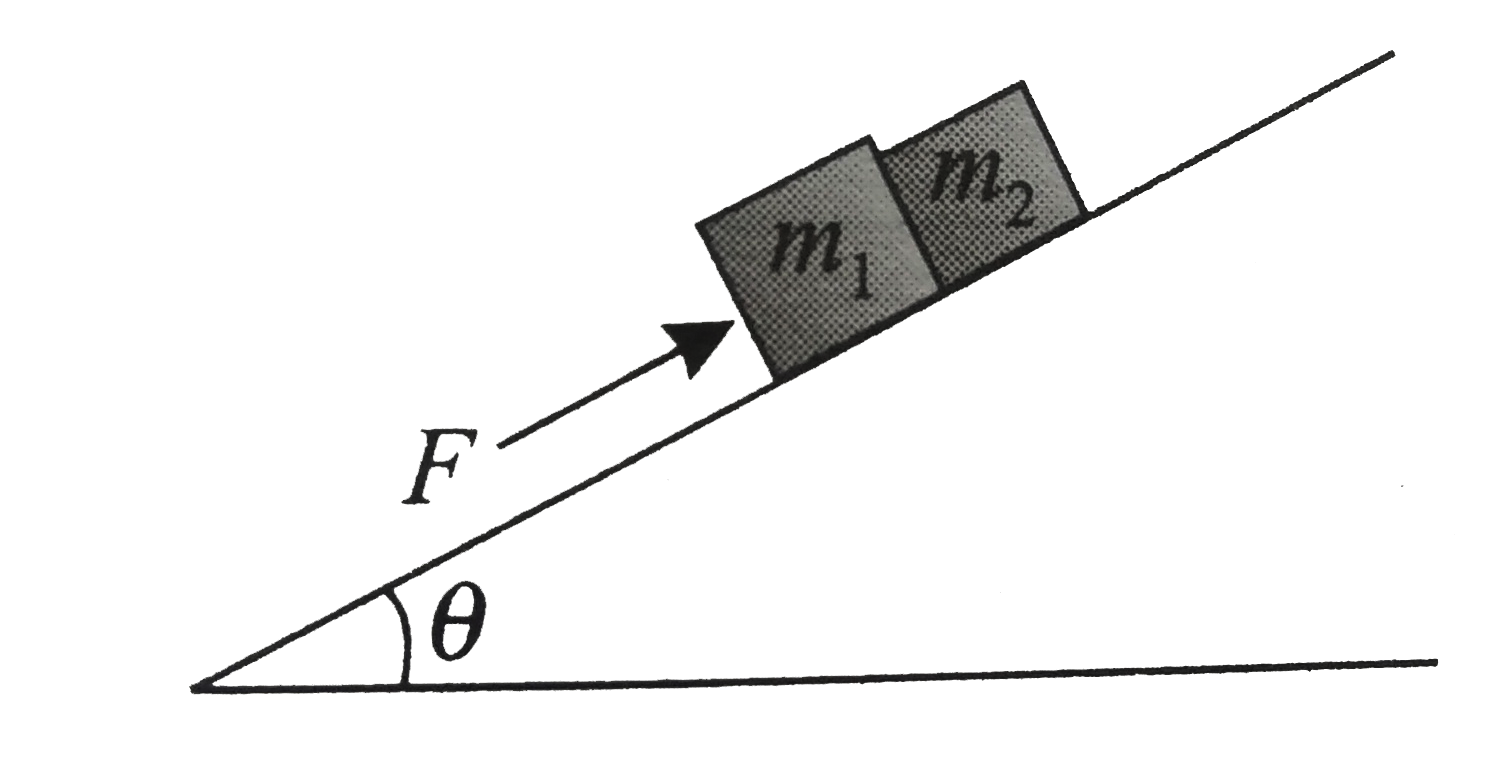
Two blocks are placed at rest on a smooth fixed inclined place. A force F acts on block of mass m1 and is parallel to the inclined plane as shown in figure. Both blocks move up the incline. Then
(i) Draw free body diagram blocks of mass m1 and blocks mass m2
(ii) Find acceleration of blocks of mass m1 and blocks mass m2
(iii) Find normal reaction between the blocks of mass m1 and m2
View SolutionA block of mass 1 kg is placed on a horizontal surface . The reaction force to the weight of the block is
View Solution
