A wheel of radius 20cm has four forces applied to it as shown in fig. Then, the torque produced by these forces about O is.
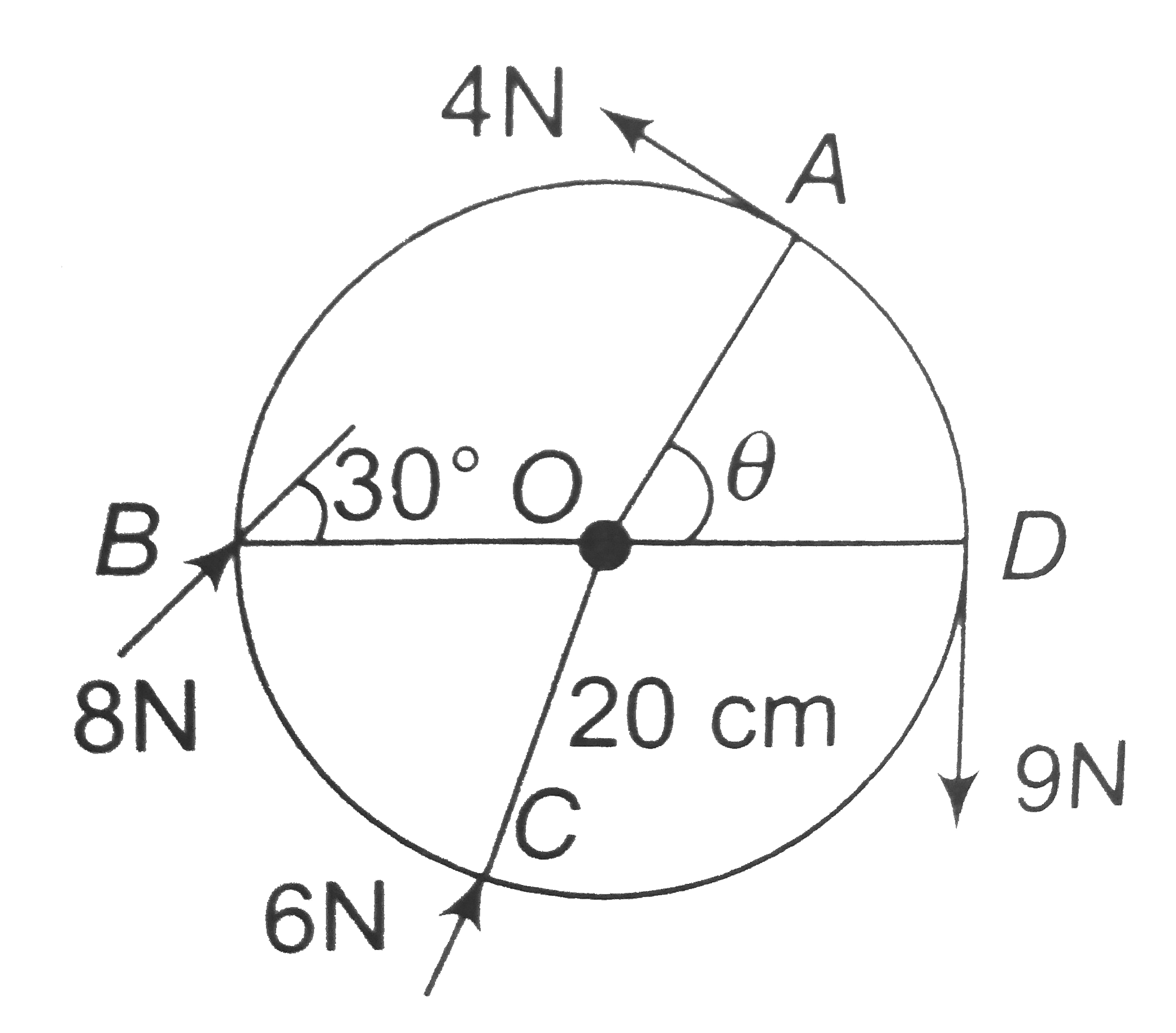 .
.
5.4Nm anticlockwise
1.8Nm clockwise
1.8Nm anticlockwise
5.4Nm clockwise
The correct Answer is:B
(b) Torque of 6N force will be zero. Net toque is
τnet=4×20100−9×20100−8sin300×20100=−1.8Nm
Negative sign shows that this torque will be clockwise.
Similar Questions
Find the torque of forces about O
(a)
(b)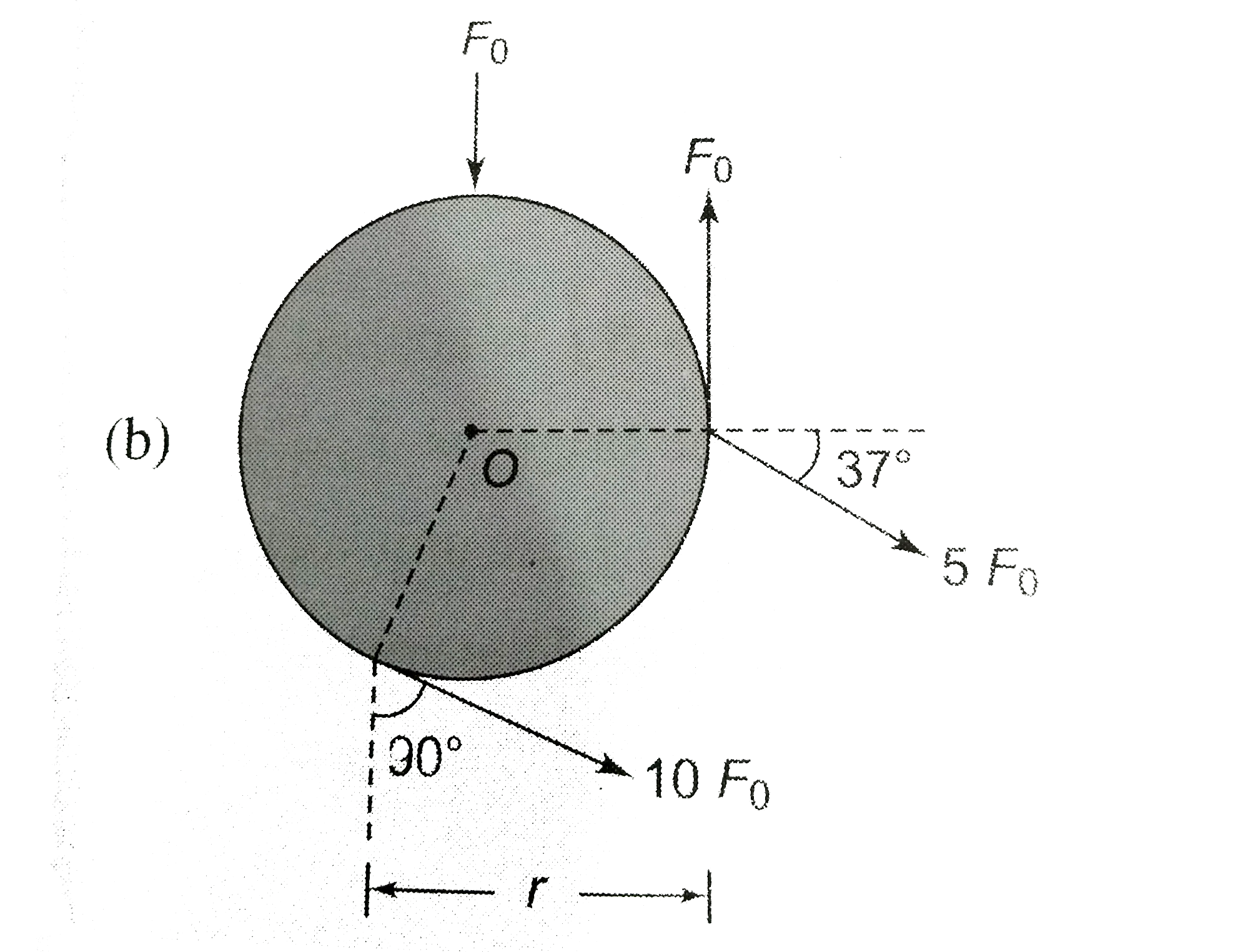
View SolutionA wheel of radius 10 cm can rotate freely about its centre as shown in figure. A stirng is wrapped over its rim and is ulle dby a force of 5.0 N. It is found that the torque roduces an angular acceleration 2.0 rads2 in the wheel. Calculate the moment of inertia of the wheel.

View Solution
Knowledge Check
A wheel of radius 20 cm has forces applied to it as shown in the figure. The torque produced by the forces 4N at A, 8N at B, 6N at C, and 9N at D at angles indicated is :
 A5.4 N-m AnticlockwiseB1.8 N-m ClockwiseC2.0 N-m ClockwiseD5.4 N-m Clockwise
A5.4 N-m AnticlockwiseB1.8 N-m ClockwiseC2.0 N-m ClockwiseD5.4 N-m ClockwiseForces are applied on a wheel of radius 20 cm as shown in the figure. The torque produced by the forces 4 N at A, 8N at B, 6 N at C and 9N at D at angles indicated is
 A5.4 N-m anti-clockwiseB1.80 N-m clockwiseC2.0 N-m clockwiseD3.6 N-m clockwise
A5.4 N-m anti-clockwiseB1.80 N-m clockwiseC2.0 N-m clockwiseD3.6 N-m clockwiseIf 100N force is applied to 10kg. block as shown in diagram then acceleration produced for slab-
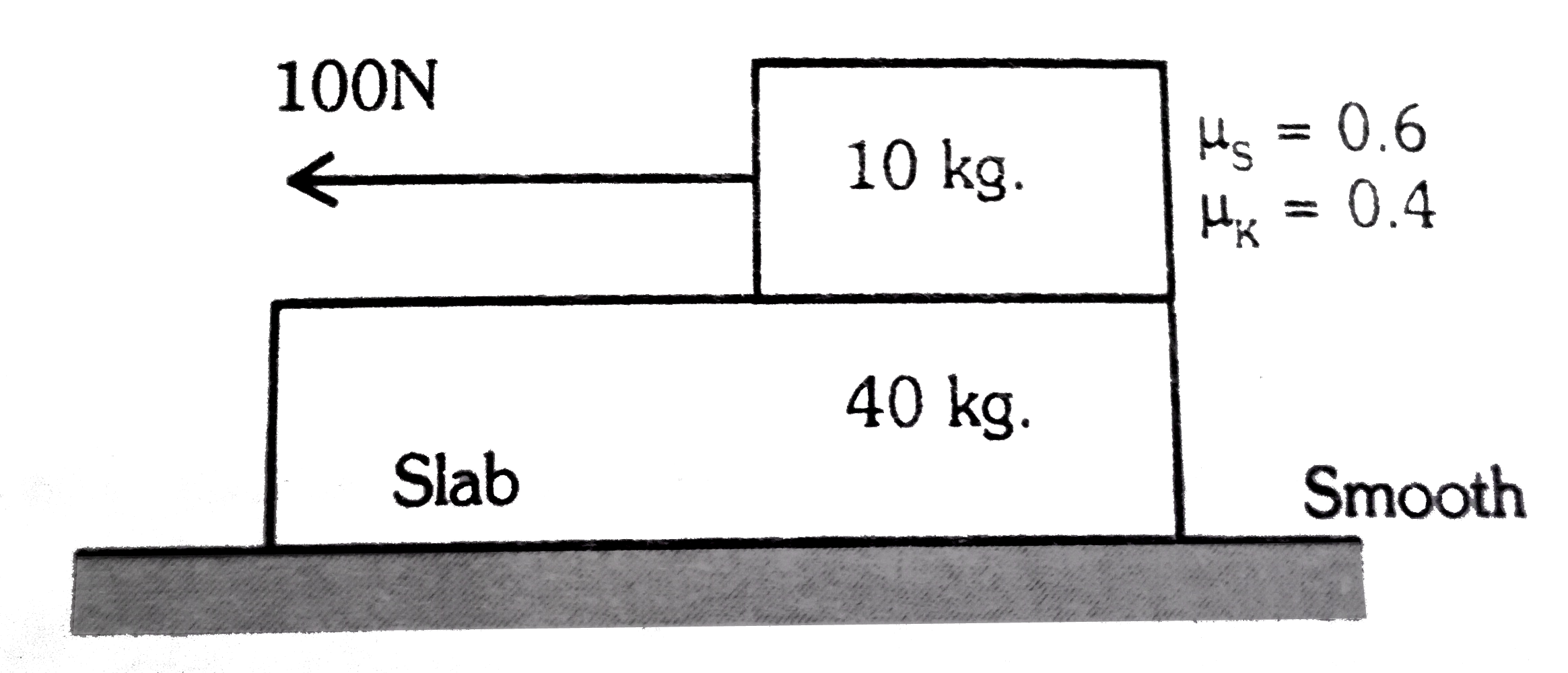 A1.65m/s2B0.98m/s2C1.2m/s2D0.25m/s2
A1.65m/s2B0.98m/s2C1.2m/s2D0.25m/s2
Different forces are applied on a pivoted scale as shown. Which of the following forces will produce torque?
View SolutionIf 100 N force is applied to 10 kg block as shown is diagram, then the acceleration produced in lower block is

View SolutionA wheel of radius R with an axle of radius R/2 is shown in the figure and is free to rotate about a frictionless axis through its centre and perpendicular to the page. Three forces (F, F, 2F) are exerted tangentially to the repective rims as shown in the figure.
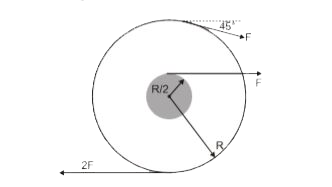
The magnitude of the net torque acting on the system is nearly
View SolutionA wheel of radius 0.4m can rotate freely about its axis as shown in the figure. A string is wrapped over its rim and a mass of 4kg is hung. An angular acceleration of 8rad/s2 is produced in it due to the torque. Then, the moment of inertia of the wheel is (g=10m/s2)

View SolutionA force Fˆk acts on O, the origin of the coordinate system. The torque of this force about the point is: (1,−1) is
View Solution
