In previous problem, the angular momentum of the projectile about the origin when it just before hits the ground should be.
−2mv3isinθsinθgˆk
mv3isinθ2cosθ2gˆk
−mv3isinθ2cosθgˆk
2mv3isinθ2cosθgˆk.
The correct Answer is:A
(a) →L2=Rˆi×m→v2, where
R=v2isin2θg=v2i(2sinθcosθ)g
=−mRvisinθˆk=−2mv3isinθsinθgˆk.
Similar Questions
Knowledge Check
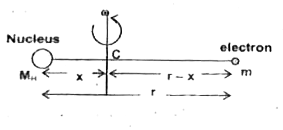
The angular momentum of the atom about the centre of mass will beAmr2ωBm(r−X)2ωC(MH+M)r2ωMHm2DMHmMH+mr2ωA particle has a linear momentum p and position vector r. the angular momentum of this particle about the origin will not be zero under the conditions
Ap=0Bp is perpendicular to r and does not cross rCp is anti-parallel to rDthe particle passes through the origin.A particle of mass m is projected with a velocity v making an angle of 45° with the horizontal. The magnitude of the angular momentum of the projectile about the point of projection, when the particle is at its maximum height h, is
AzeroBmv34√2gCmv3√2gDm√2gh3
A particle of mass m has been thrown with intial speed u making angle θ with the horizontal ground. Find the angular momentum of the projectile about an axis perpendicular to the plane and passing through the point of projection when the projectile is
(a) At the highest point
(b) About to hit the ground
View SolutionIn the previous problem 3 the magnitude of the momentum transferred during the hit is .
View SolutionA projectile of mass m is launched with an initial velocity →vi making an angle θ with the horizontal as shown in figure. The projectile momentum of the particle about the origin when it is at the highest point of its trajectory is.
 .
.
View SolutionA particle of mass 1kg has been thrown with initial speed 20 ms making an angle 60° with the horizontal ground. the angular momentum of the particle about point of projection when the projectile is at highest point is (g=10m/s^2)
View SolutionA projectile is fired with velocity u making an angle θ with the horizontal. What is the angular momentum of the projectile at the highest point about the starting point ? (Given the mass of the projectile is m )
View Solution

