An cylinder of mass m is rotated about its axis by an angular velocity ω and lowered gently on an inclined plane as shown in figure. Then :
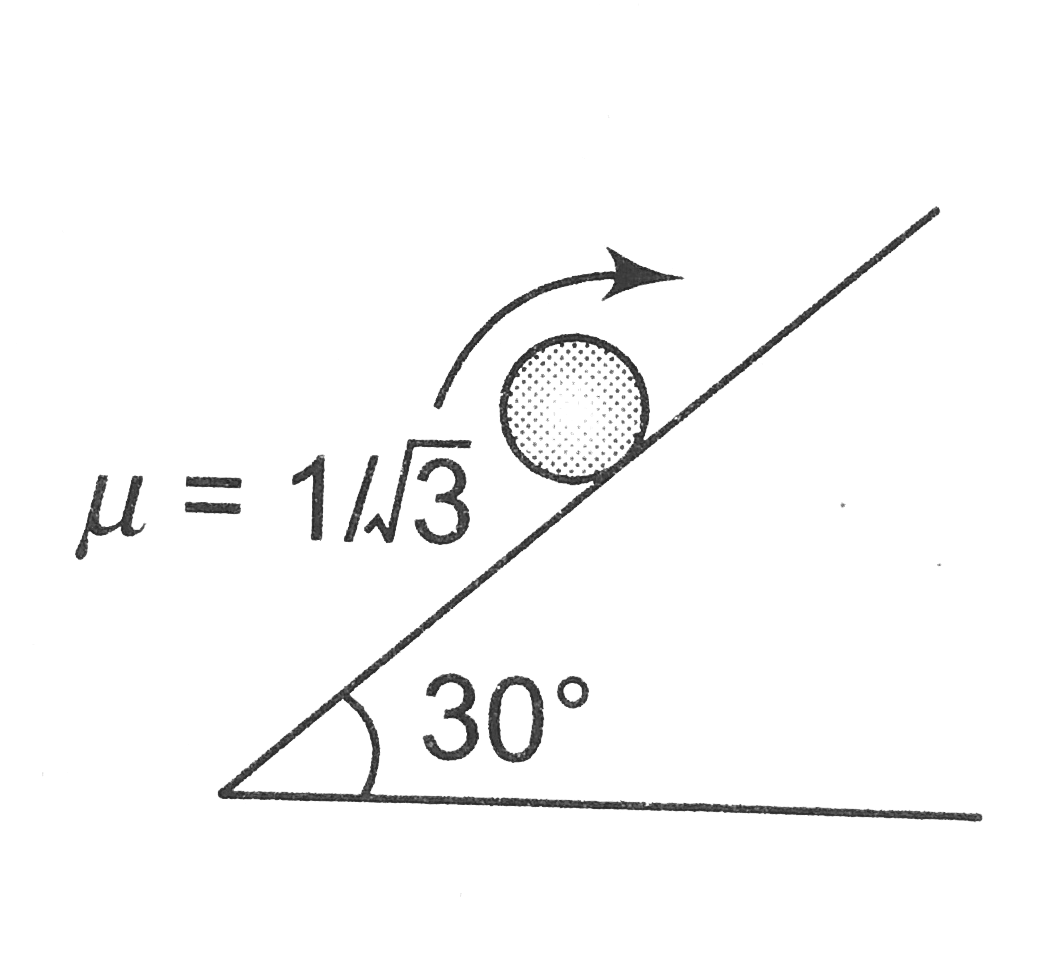 .
.
it will start going upward
it will first going upward and then downward
it will go downward just after it is lowered
it can never go upward.
The correct Answer is:D
(d) Since net force along the incline is zero, so cylinder will remain in position till it stops rotating. After that it will start moving downwards.
Similar Questions
Knowledge Check
A sphere of mass m is rotated about its axis by an angular velocity ω and lowered gently on an inclined plane as shown in figure. Then initally
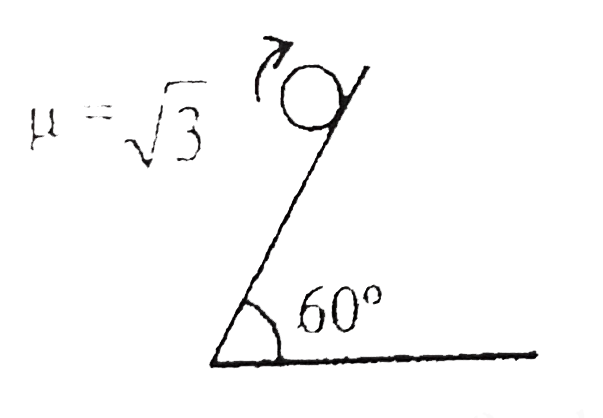 Athe centre of mass of sphere accelerates upwards.Bthe centre of mass of shpere accelerates downwardsCthe lowest point of contact accelerates upwards.Dthe lowest point of contect accelerates downwards.
Athe centre of mass of sphere accelerates upwards.Bthe centre of mass of shpere accelerates downwardsCthe lowest point of contact accelerates upwards.Dthe lowest point of contect accelerates downwards.A disc is rotated about its axis with a certain angular velocity and lowered gently on a rough inclined plane as shown in Fig., then
 AIt will rotate at the position where it was placed and then will move downwardsBIt will go downwards just after it is loweredCIt will go downwards first and then climb upDIt will climb upwards and then move downwards
AIt will rotate at the position where it was placed and then will move downwardsBIt will go downwards just after it is loweredCIt will go downwards first and then climb upDIt will climb upwards and then move downwardsA non-conducting disk of radius R is rotating about its own axis with constant angular velocity ω in a perpendicular uniform magnetic field B as shown in figure. The emf induced between centre and rim of disk is
 ABωR22BBωR2CZeroDBωR23
ABωR22BBωR2CZeroDBωR23
A solid cylinder of mass 20kg rotates about its axis with angular velocity of 100 radian s−1. The radius of the cylinder is 0.25m. The magnitude of the angular momentum of the cylinder about its axis of rotation is
View SolutionA cylinder of mass m radius R is spined to a clockwise angular velocity ωo and then gently placed on an inclined plane for which coefficient of friction μ=tanθ,θ is the angle of inclined plane with the horizontal. The centre of mass of cylinder will remain stationary for time

View SolutionA solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
View SolutionA circular disc of radius R is rotating about its axis O with a uniform angular velocity ωrad s−1 as shown in the figure. The magnitude of the relative velocity of point A relative to point B on the disc is

View SolutionA circular of radius 20 cm is rotating about its own axis at an angular velocity ω . The angular velocity of a particle 'A' which is at a distance 10 cm from the axis of rotation is
View Solution
