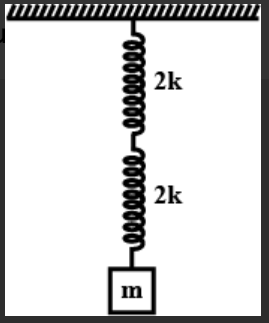
A system is shown in the figure. The force The time period for small oscilations of the two blocks will be

2π√3mK
2π√3m2K
2π√3m4K
2π√3m8K
The correct Answer is:C
Both the spring are in series
∴Keq=K(2k)K+2K=2K3
Time period
T=2π√μKeqwhereμ=m1m2m1+m2
Here μ=m2
∴T=2π√m2.32K=2π√3m4K.
Similar Questions
Knowledge Check
The time period of small oscillations of mass m :-
_S01_040_Q01.png) A2π√m6kB2π√11m6KC2π√6m11KD2π√mK
A2π√m6kB2π√11m6KC2π√6m11KD2π√mKA block of mass m is connected to two indentical springs of spring constant k which are in turn connected to fixed supports as shown in the figure. Find the time period for small oscillations of the block.
 A2π√mkB2π√m2kC2π√2mkDπ√m2k
A2π√mkB2π√m2kC2π√2mkDπ√m2kA block of mass 'm' is released on the top of a frictionless incline as shown in the figure. The time period of the oscillation of the block is
 A2π√mK+√2LsinθgB2π√mK+√2(L−l)gsinθC2π√(L−l)gsinθ+√mKDnone of these
A2π√mK+√2LsinθgB2π√mK+√2(L−l)gsinθC2π√(L−l)gsinθ+√mKDnone of these
Find time period of oscillation of the system.

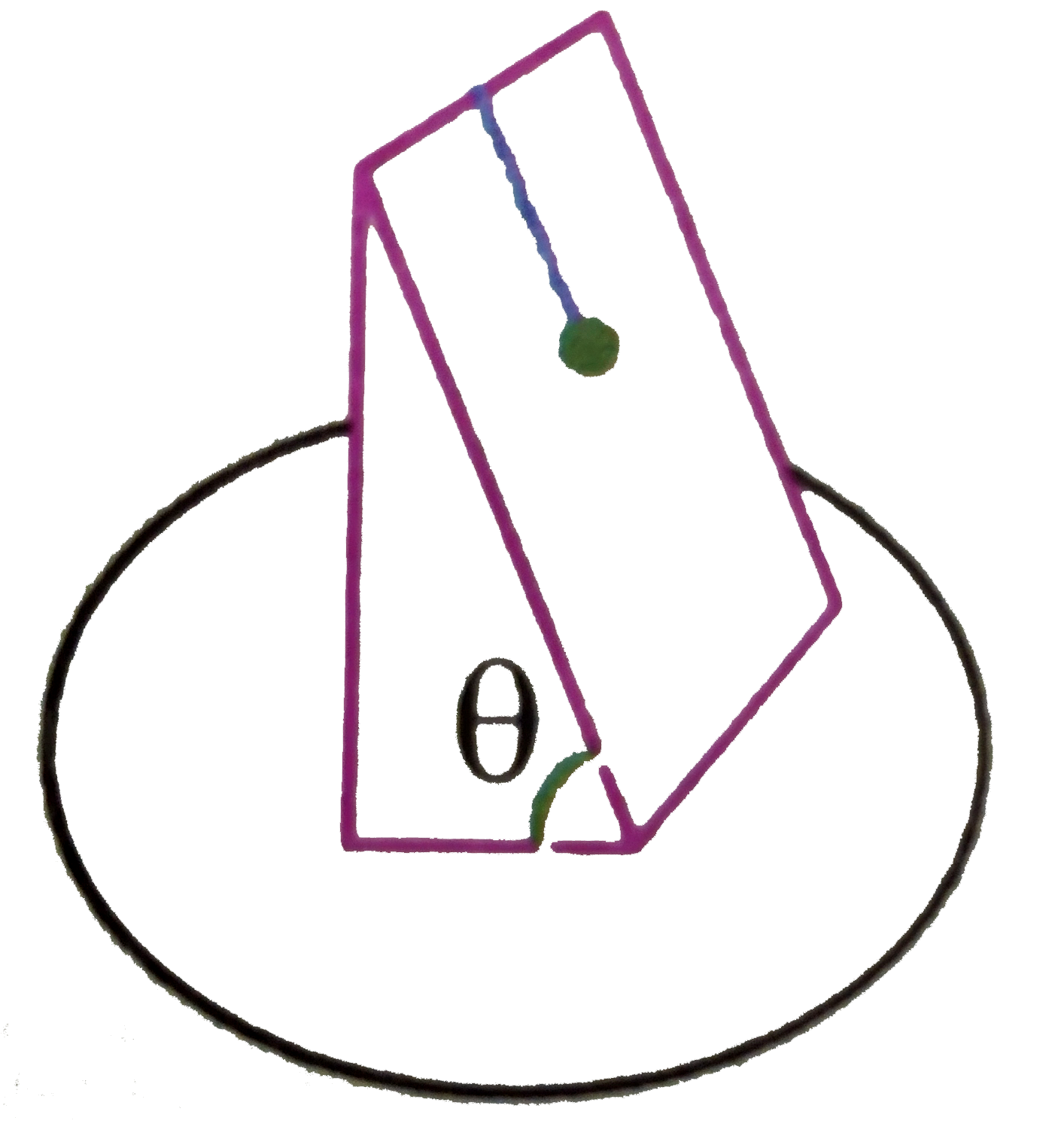
View SolutionA small particle is tied by the help of two strings to vertical walls with the parameters as shown in the figure (g=π2). The time period of the small oscillations of the particle if it is displaced perpendicular to the plane of the paper slightly is x sec, the value of x is ____________

View SolutionThere is a system of infinite pulleys and springs.Spring constants are in GP as k 2k 4k 8k.........oo as shown in the figure.All the pulleys are massless frictionless and strings are massless and inextensible.Then time period of small oscillations of the block will be (Mass of block is m ). qquad (in ) (i) 2
View SolutionIn the diagram shown find the time period of pendulum for small oscillations
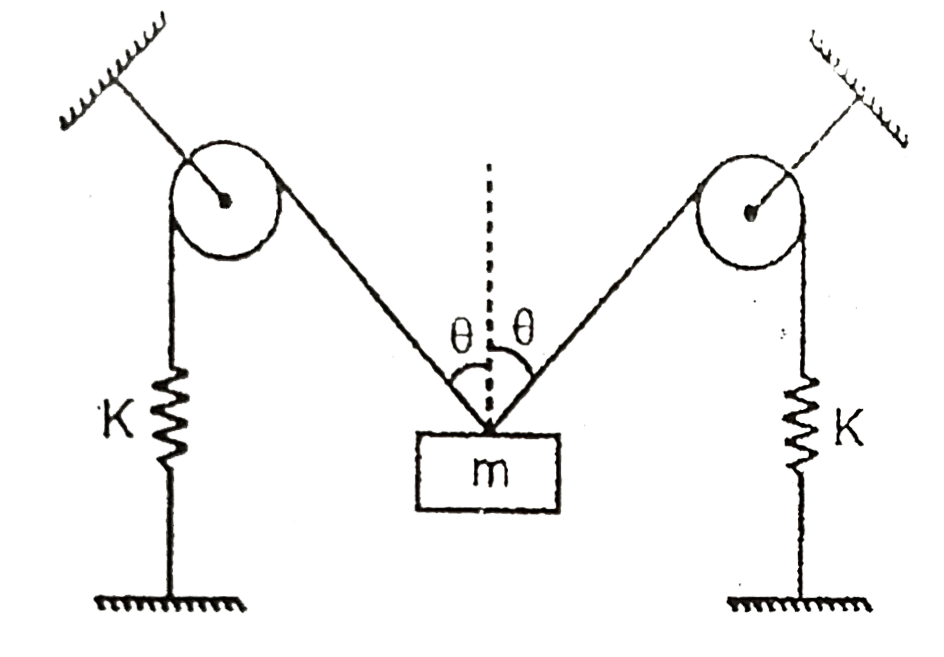
View SolutionIn the situation as shown in figure time period of small vertical oscillation of block will be - (String, springs and pulley are ideal)
View Solution