A whistle revolves in a circle with an angular speed of 20rad/sec using a string of length 50cm. If the frequency of sound from the whistle is 385Hz, then what is the minimum frequency heard by an observer which is far away from the centre in the same plane? v=340m/s
333Hz
374Hz
385Hz
394Hz
The correct Answer is:B
To solve the problem, we need to determine the minimum frequency heard by an observer when a whistle is revolving in a circle. We will use the Doppler effect formula for sound.
Given Data:
- Angular speed, ω=20rad/s
- Length of string (radius), r=50cm=0.5m
- Frequency of sound from the whistle, f0=385Hz
- Speed of sound, v=340m/s
1. Calculate the linear speed of the whistle (source):
The linear speed vs of the whistle can be calculated using the formula:
vs=r⋅ω
Substituting the values:
vs=0.5m⋅20rad/s=10m/s
2. Identify the observer's position:
The observer is positioned far away from the center of the circle, in the same plane as the whistle. Since the whistle is moving away from the observer at the point of minimum frequency, we will use the Doppler effect formula for a source moving away from a stationary observer.
3. Apply the Doppler effect formula:
The formula for the frequency heard by the observer when the source is moving away is given by:
f′=f0⋅vv+vs
Where:
- f′ is the frequency heard by the observer,
- f0 is the emitted frequency,
- v is the speed of sound,
- vs is the speed of the source.
4. Substituting the values:
Now, substitute the known values into the formula:
f′=385Hz⋅340m/s340m/s+10m/s
f′=385Hz⋅340350
5. Calculating the frequency:
Now calculate the fraction:
f′=385Hz⋅3435
f′=385Hz⋅0.9714≈374Hz
Final Answer:
The minimum frequency heard by the observer is approximately 374Hz.
---
- Angular speed, ω=20rad/s
- Length of string (radius), r=50cm=0.5m
- Frequency of sound from the whistle, f0=385Hz
- Speed of sound, v=340m/s
The linear speed vs of the whistle can be calculated using the formula:
vs=r⋅ω
Substituting the values:
vs=0.5m⋅20rad/s=10m/s
The observer is positioned far away from the center of the circle, in the same plane as the whistle. Since the whistle is moving away from the observer at the point of minimum frequency, we will use the Doppler effect formula for a source moving away from a stationary observer.
The formula for the frequency heard by the observer when the source is moving away is given by:
f′=f0⋅vv+vs
Where:
- f′ is the frequency heard by the observer,
- f0 is the emitted frequency,
- v is the speed of sound,
- vs is the speed of the source.
Now, substitute the known values into the formula:
f′=385Hz⋅340m/s340m/s+10m/s
f′=385Hz⋅340350
Now calculate the fraction:
f′=385Hz⋅3435
f′=385Hz⋅0.9714≈374Hz
The minimum frequency heard by the observer is approximately 374Hz.
Similar Questions
A whistle revolves in a circle with angular speed ω = 20 rad/sec using a string of length 50 cm . If the frequency of sound from the whistle is 385 Hz, what is the minimum frequency heard by an observer which is far away from the centre. Velocity of sound in air is 340 m/s
View SolutionA whistle revolves in a circle with angular speed 0 = 20 rad/sec using a string of length 50 cm. If the frequency of sound from the whistle is 385 Hz, then what is the minimum frequency heard by an observer which is far away from the centre? (velocity of sound = 340 m/s)
View SolutionA whistle emitting a sound of frequency 440 Hz is tied to a string of 1.5 m length and roated with an angular velocity of 20 rad//s in the horizontal plane. Calculate the range of frequencies heard by an observer stationed at a larger distance from the whistle .(Speed of sound = 330 m//s) .
View SolutionA whistle revolves in a circle with an angular speed of 20rad/sec using a string of length 50cm. If the frequency of sound from the whistle is 385Hz, then what is the minimum frequency heard by an observer which is far away from the centre in the same plane? v=340m/s
View SolutionA whistle emitting a sound of frequency 440 Hz is tied to a string of 1.5 m length and rotated with an angular velocity of 20 rad/s in the horizontal plane. Then the range of frequencies heard by an observe stationed at a large distance from the whistle will be (v=330 m/s)
View Solution(i) What is beat phenomenon?
(ii) A whistle revolves in a circle with angular velocity of ω=20rads−1. If the frequency of sound is 385 Hz and speed is 340 ms−1, then find the frequency heard by the observer when the whistle is at B.
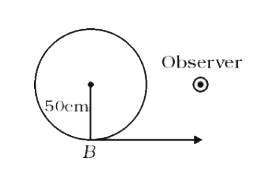
View SolutionA whistle revolves in a circle with an angular speed of 20 rad//sec using a string of length 50 cm . If the frequency of sound from the whistle is 385 Hz , then what is the minimum frequency heard by an observer which is far away from the centre in the same plane? v=340m//s
View Solution
A whistle emitting a sound of frequency 440Hz is tied to string of 1.5m length and rotated with an angular velocity of 20rad/sec in the horizontal plane. Then the range of frequencies heard by an observer stationed at a large distance from the whistle will (v=330m/s)
View Solution
