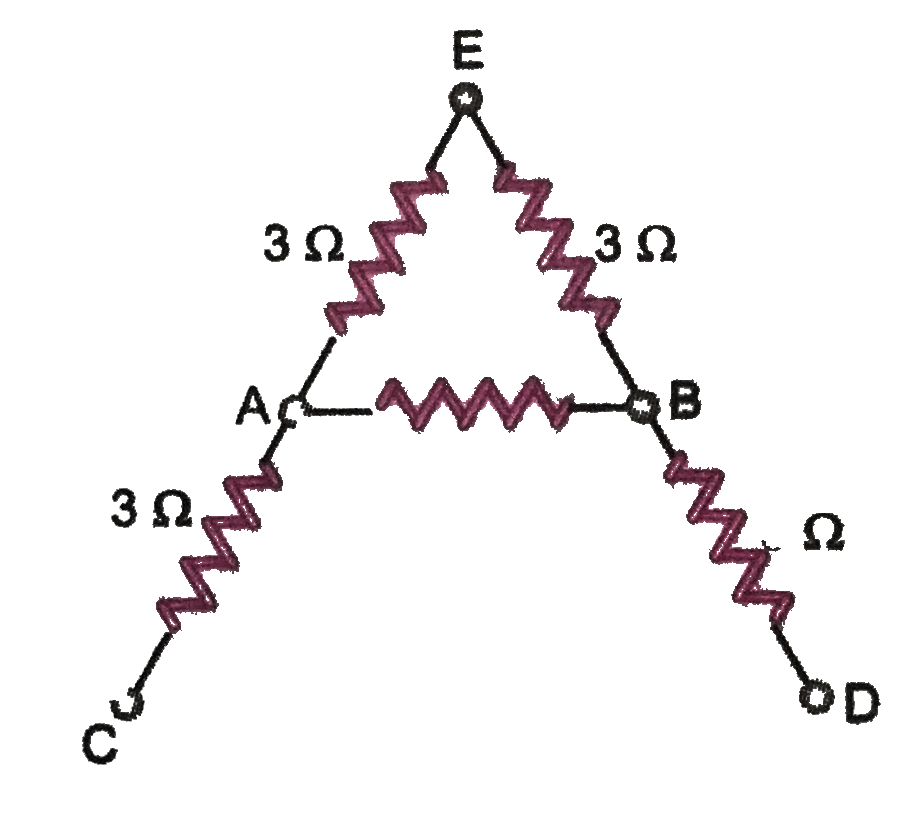
Five resistors, each 3Ω, are connected as shown in (fig. 3.23). Calculate the resistance between the points
(a) A and b
between the point CandD.
 .
.
Video Solution
Text Solution
The correct Answer is:(a) 2Ω
(b) 8Ω.
(i) In (Fig. 3.23), resistance in the arm AEB, i.e., R1=3Ω+3Ω=6Ω
As R1(=6Ω)and3Ω (in arm AB) are in parallel, effective resistance between the points AandB, i.e.,
R=6×36+3Ω=2Ω
(ii) Since the effective resistance between points AandB(i.e.,2Ω) and in the arm AC(=3Ω) and arm BD(=3Ω) are in series, effective resistance between the points CandD=2+3+3=8Ω.
|
Similar Questions
Knowledge Check
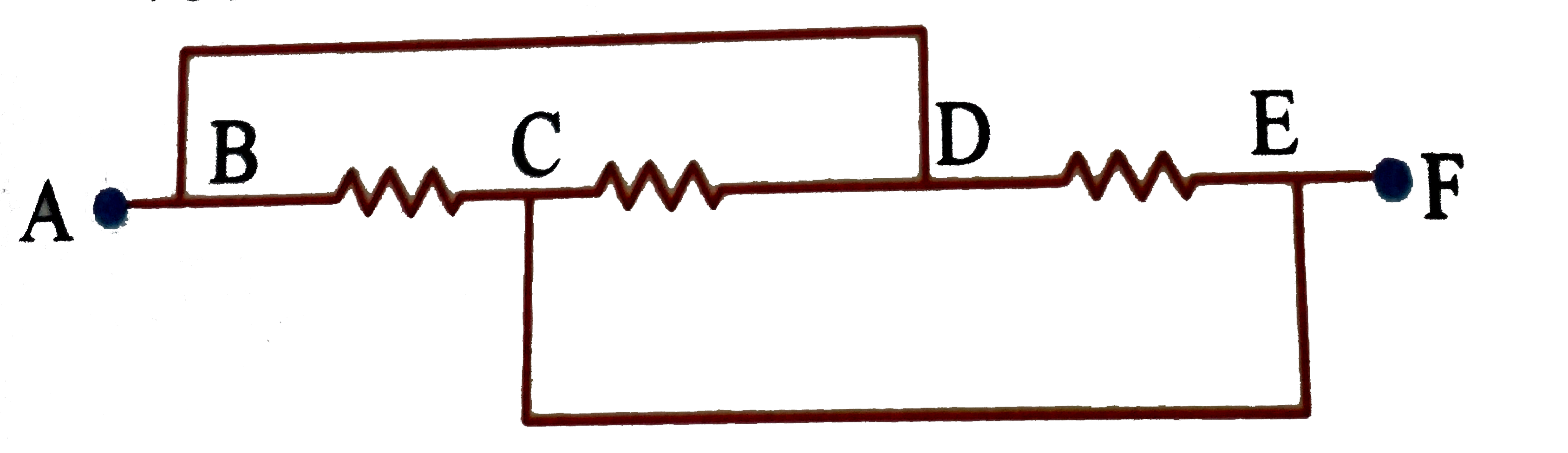
Three resistances each of 3Ω are connected as shown in fig. the resultant resistance between A and F isA9ΩB2ΩC4ΩD1ΩFive resistance, each of 5Ω are connected as shown in figure. Find the equivalent resistance between points (1) A and B , (2) A and C .
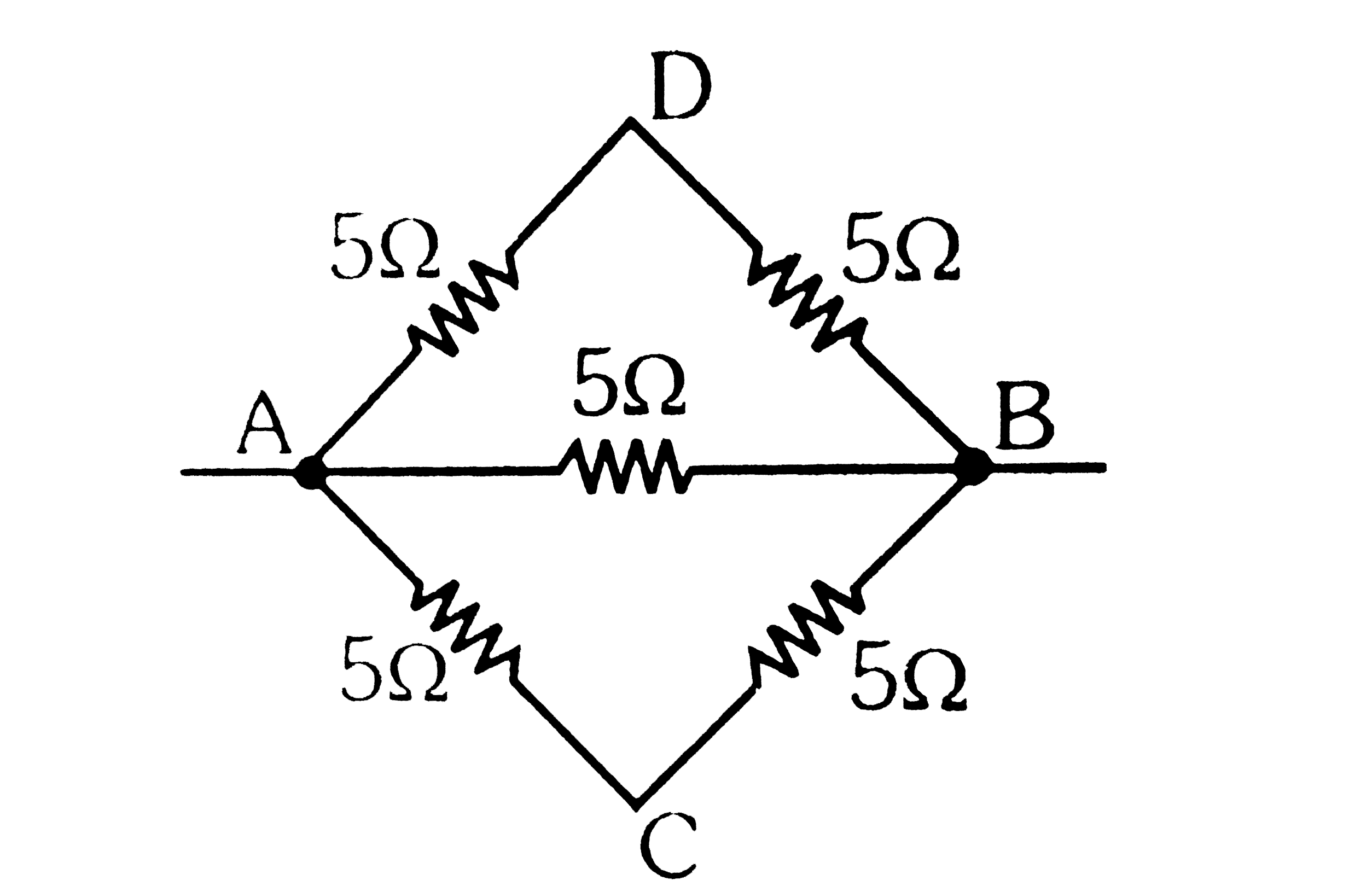 A(1) 7.5Ω (2) 2.25ΩB(1) 5Ω (2) 2.50ΩC(1) 2.5Ω (2) 3.13ΩD(1) 3Ω (2) 2.5Ω
A(1) 7.5Ω (2) 2.25ΩB(1) 5Ω (2) 2.50ΩC(1) 2.5Ω (2) 3.13ΩD(1) 3Ω (2) 2.5ΩFive resistances are connected as shown in the figure. The effective resistance between the points A and B is
 A103ΩB203ΩC15ΩD6Ω
A103ΩB203ΩC15ΩD6Ω
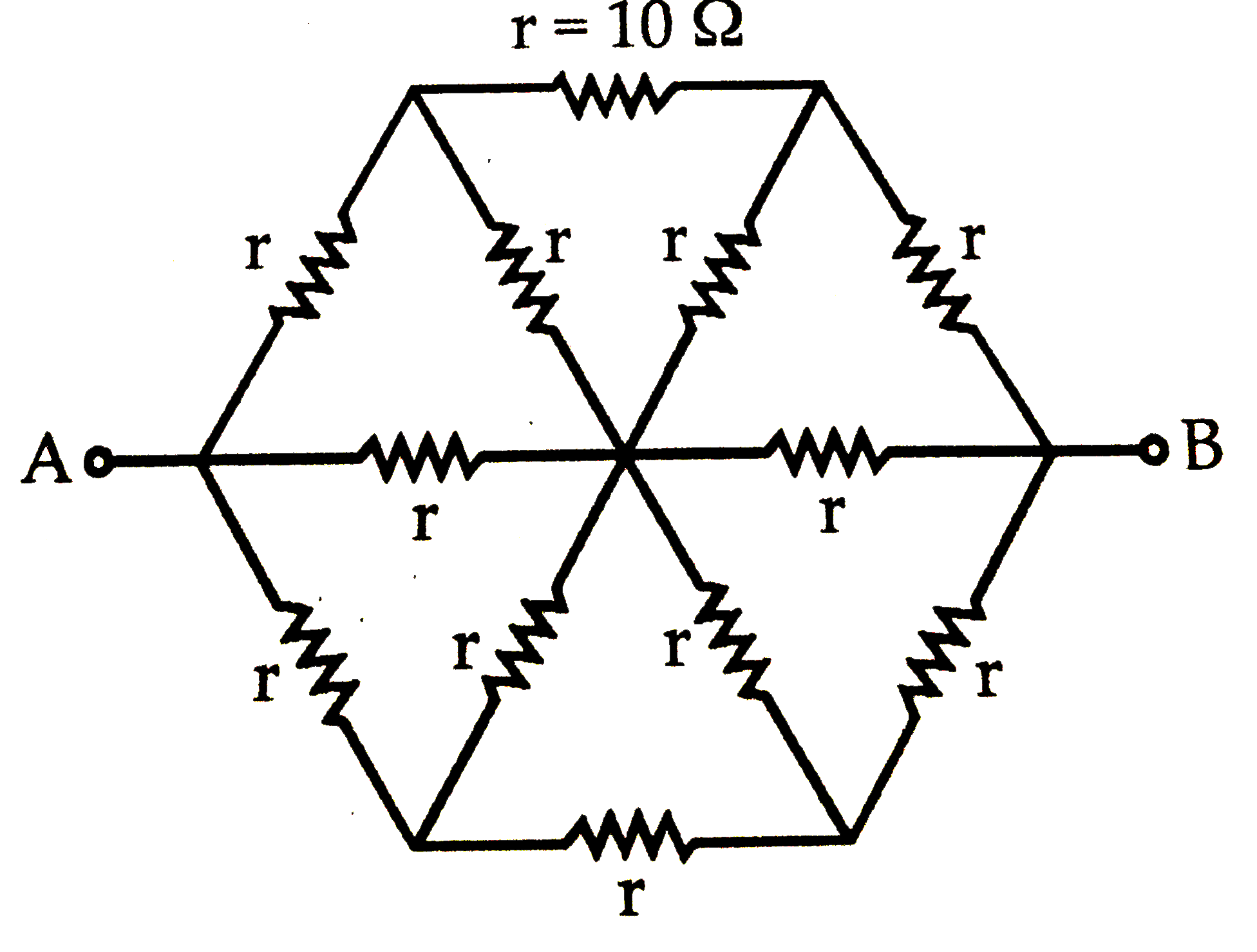
Five resistance are connected as shown in fig. The effective resistancebetween the points A and B is
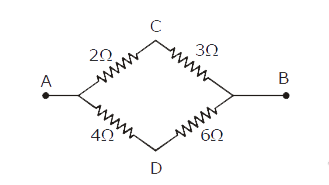
View SolutionIdnetical resistor each of resistance r are connected as shown in figure. Calculate equivalent resistance between A and E.
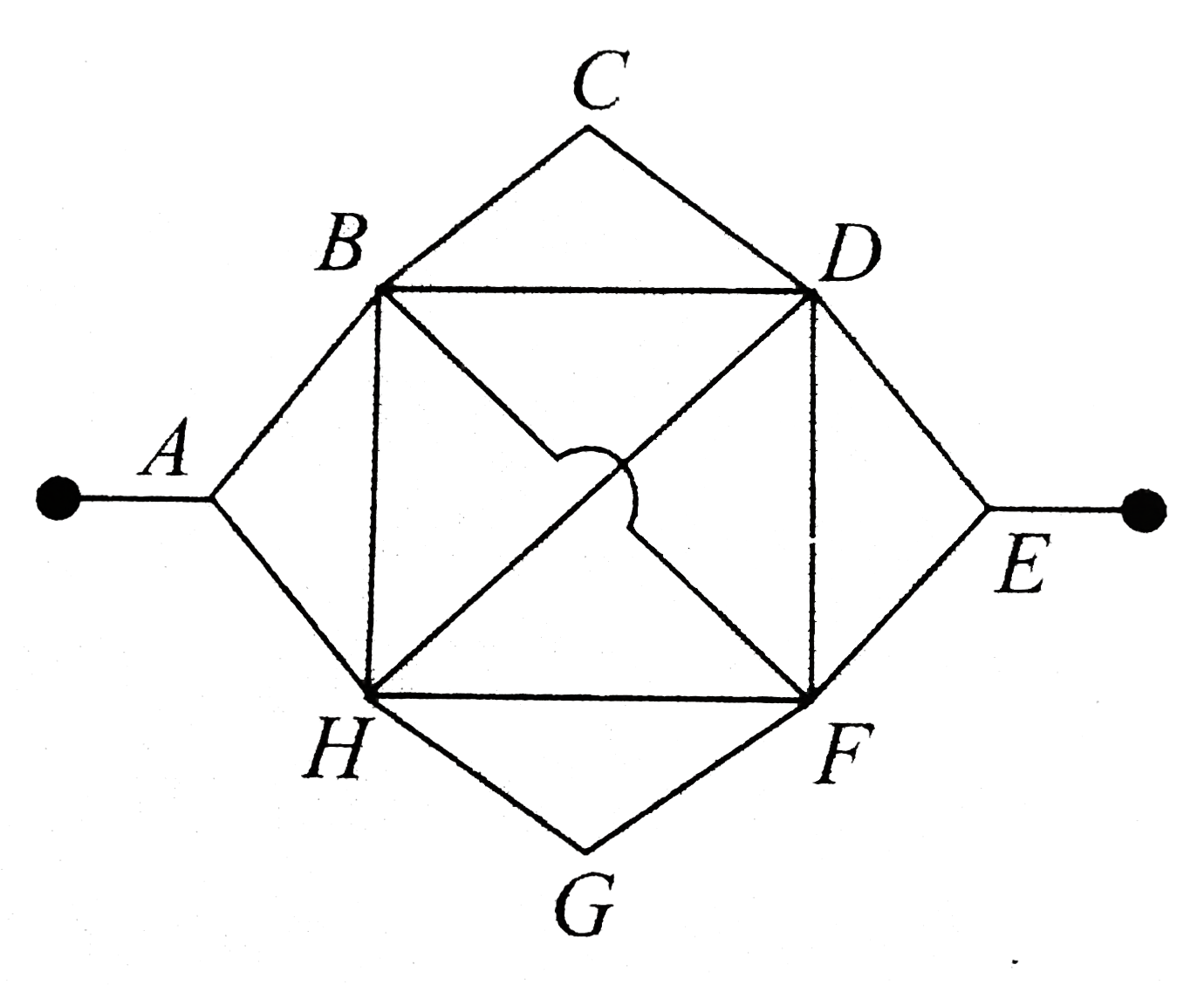
View SolutionFive resistors are connected as shown in figure. Find the equivalent resistance between the points B and C.
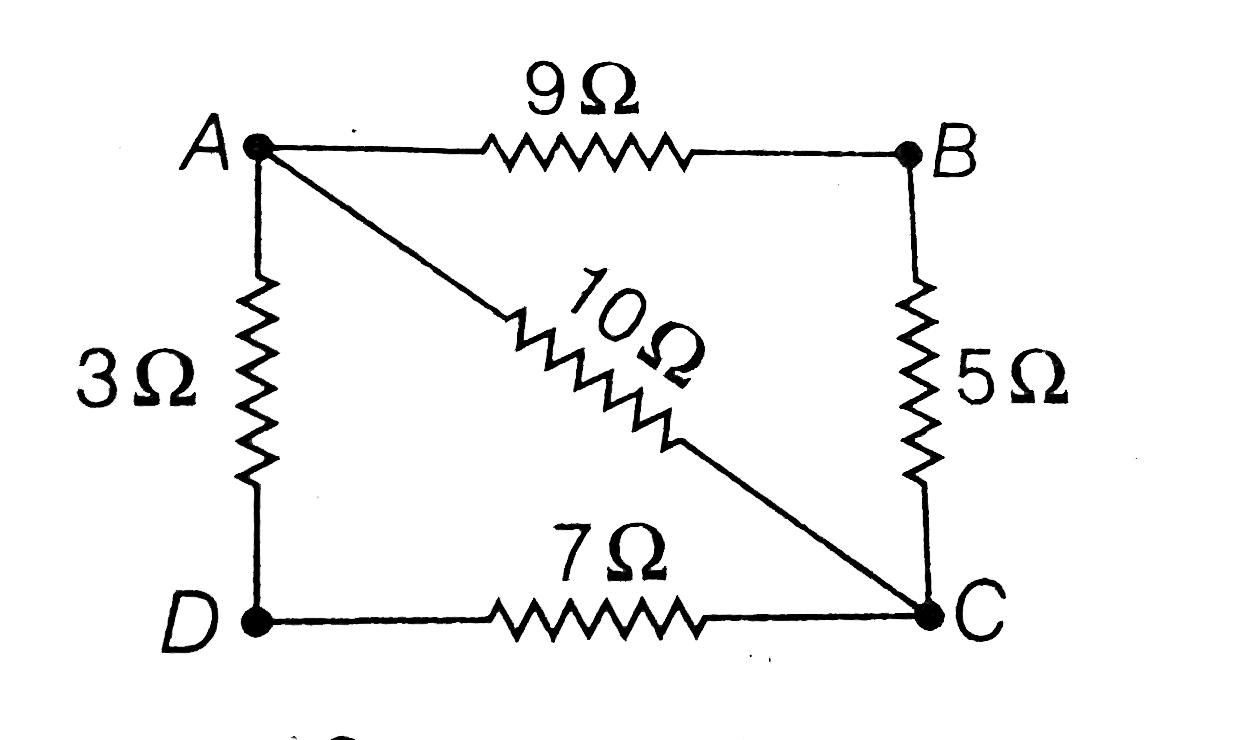
View SolutionFive resistance are connected as shown in the figure. The equivalent resistance between points A and C is
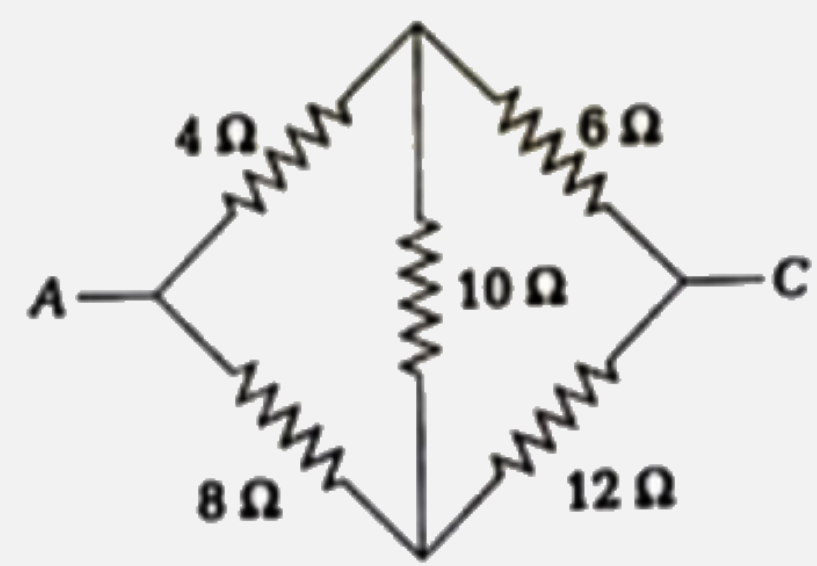
View Solution
Resistance of each 10Ω are connected as shown in the fig. The effective resistance between A and G is
View Solution