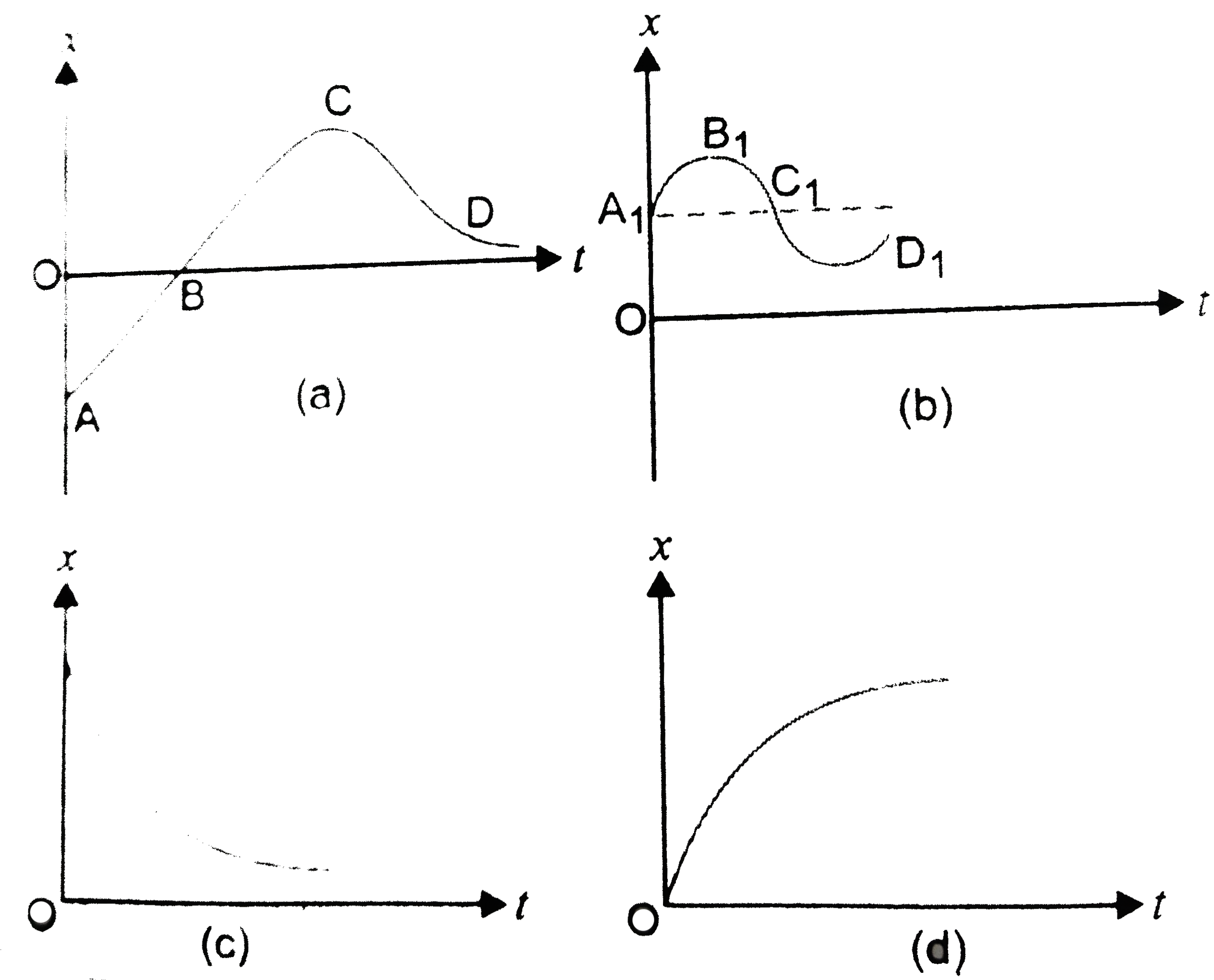
Refer to the graphs fig. 2 (EP).5 Match the following.
Graph Characteristic
(a) (i) has v>anda<o throughout.
(b) (ii) has x>0 throughout and has a point with v=0 and a point with a=0.
(c ) (ii) has a point with zero displacement for t>0.
(d) (iv) has v<anda>0.
Video Solution
Text Solution
(a−iii),(b−ii),(c−iv),(d−i).
For graph (a). There is a point (B) for which displacementis zero for t>0, which is option (iii). For graph (b), the condition x>0 throughout. There is a point B1 at the top of the curve, where slope of the curve, i.e., dx/dt=v=0 and there is a point C1 on curve, wher the curvature of curve chages, which show, acceleration=0. This corresponds to option (ii).
For graph (c ), the slope (dx//dt) is negative, hence v<0. The curvature of x−t graph indicates that the begative velocity (=dx//dt) is decreasing with time. Therefore, a>0. This corresponds to option (iv).
For graph (d), the slope (=dx//dt) is poitive, hence v>0. The curvature of x−t graph indicates that positive velocity is decreasing with time. Therfore, a<0. This corresponds to option (i).
|
Similar Questions
Knowledge Check
Referring to Fig (i) and (ii0, match the following
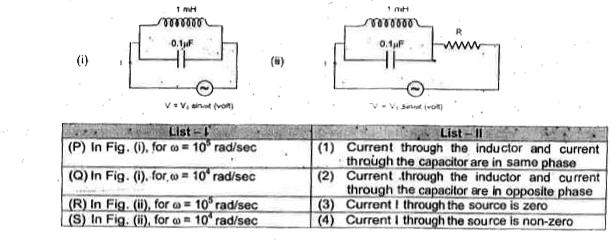 APQRS2.32.42.32.4BPQRS1.324.23CPQRS432.12.3DPQRS3.14.112
APQRS2.32.42.32.4BPQRS1.324.23CPQRS432.12.3DPQRS3.14.112If the conductor has V≠0 with zero charge then:
Athere cannot be any charge in the body of conductorBthere must be charge on the surface or inside itselfCthere must be charge only on the surfaceDboth (a) and (b)If a<0andb>0 then the point (a, b) lies in quadrant
AIVBIICIIIDNone of these
If a<0,b>0and c<0, then the point P(a,b,−c) lies in the octant
View SolutionA random variable X has the following probability distribution:

Determine (i)k,(ii)P(X<3),(iii)P(0<X<3),(iv)P(X>4).
View SolutionPlot each of the following points on a graph paper:
(i) (-3, 0)
(ii) (3, 0)
(iii) (0, -3)
(iv) (0, 3)
View SolutionIf c>0and4a+c<2b. Then ax2−bx+c=0 has a root in which one of the following intervals ?
View SolutionLet a ∈ R and f : R→R be given by f(x)=x5−5x+a, then
(a) f(x)=0 has three real roots if a>4
(b) f(x)=0 has only one real root if a>4
(c) f(x)=0 has three real roots if a<−4
(d) f(x)=0 has three real roots if −4<a<4
View Solution
