A small particle of mass m is projected at an angle θ with x-axis with initial velocity υ0 in x-y plane as shown in Fig. Calculate the angular momentum of the particle
at t<υ0sinθg.

mgv0tcosθˆk
−12mgv0t2cosθˆk
12mgv0t2cosθˆi
−mgv0t2cosθˆj
The correct Answer is:B
Let the particle projectied from (O) reach (P) in time (t) with velocity →v=(vxˆI+ˆI+vyˆj) and corrdinates of (P) be ( x, y)
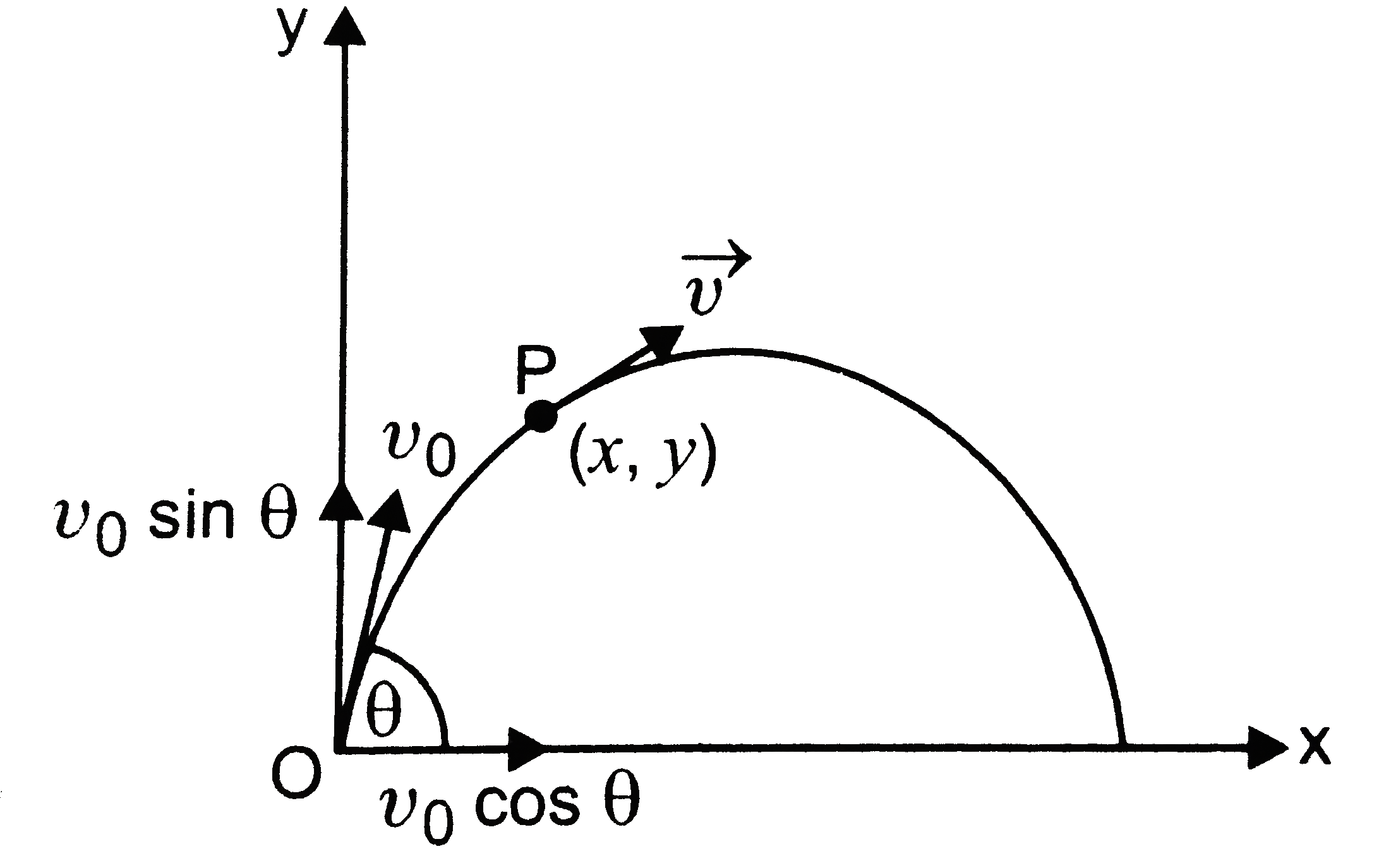 .
.
Then vx=v0cosθ,v_y = v_0 sin theta - gt<br> x = v_0 cos thetat, y= v_0 isn theta t - 1/2 gt^@<br>vec r = ( a hat i+ y hat j)<br>Momentumofpartic≤at(P)aboutorig∈(O)is.
→L=→r×→p=(xˆi+yˆj)×m(vxˆi+vyˆj)
=myvx(−ˆk)+mxvy(ˆk)
=m(v0sinθt12>2)v0cosθ(−ˆk)
+m(v0cosθt)(v0sinθ−>)(ˆk)<br> =- mv_0^2 cos theta sin t hat k + me_0 cos theta xx 1/2 gt^2 hat k<br>+ mv_0^2 sin theta cos theta cos thea t hat k - mv-0 cos theta gt^2 hat k<br> =- 1/2 m v_0 gt^2 cos theta hat k .
Similar Questions
A small particle of mass m is projected at an angle θ with x-axis with initial velocity υ0 in x-y plane as shown in Fig. Calculate the momentum of the particle
at t<υ0sinθg.

View SolutionA small particle of mass m is projected at an angle θ with the x-axis, with initial velocity v0 in the x-y plane. Just before time 2v0sinθg , the angular momentum of the particle about the point of projection is
View Solution
Knowledge Check
A small particle of mass m is projected at an angle θ with the x- axis with an initial velocity v0 in the x−yplane as shown in the figure . At a time t<v0sinθg, the angular momentum of the particle is
where ˆi,ˆjandˆk are unit vectors along x,yandz - axis respectively.
 A−mgv0t2cosθˆjBmgv0tcosθˆkC−12mgv0t2cosθˆkD12mgv0t2cosθˆi
A−mgv0t2cosθˆjBmgv0tcosθˆkC−12mgv0t2cosθˆkD12mgv0t2cosθˆiA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?
 AmvLBmvlCmvrDzero
AmvLBmvlCmvrDzeroA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?
 AmvLBmvlCmvrDZero
AmvLBmvlCmvrDZero
A particle of mass m is projected at t=0 from the point P on the ground with speed v0 at an angle of θ to the horizontal. Find the magnitude and direction of the angular momentum of the particle at time t=v0sinθ2g.
View SolutionIf the particle of mass m is moving with constant velocity v parallel to x-axis in x-y plane as shown in (figure), Find its angular momentum with respect of origin at any time t.

View SolutionA particle of mass m is projected from origin O with speed u at an angle θ with positive x-axis. Positive y-axis is in vertically upward. Direction. Find the angular momentum of particle at any time t about O before the particle strkes the ground again.
View SolutionA projectile is projected with a velocityv0 at an angle θ with the horizontal as shown in figure. The angular momentum of particle about the origin:

View SolutionIf a particle of mass m is moving with constant velocity v parallel to x-axis in x−y plane as shown in fig. Its angular moment with respect to origin at any time t will be
View Solution
