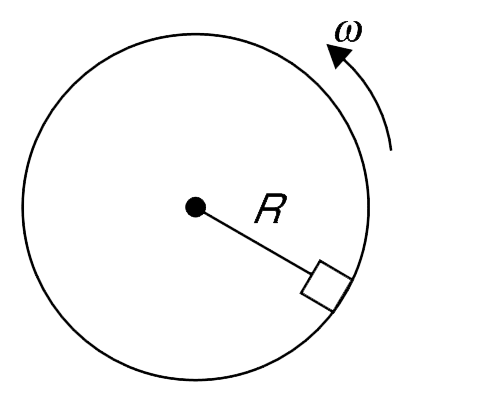
A cylinder of radius R is rotating about its horizontal axis with constant ω=√5gR. A block of mass m is kept on
the inner surface of the cylinder. Block is moving in vertical circular motion without slipping. co–efficient of friction between block and surface of cylinder is μ. If minimum value of μ for complete vertical circular motion of block is 2√63x then find 'x'.

N=mgcosθ+mω2R=mgcosθ+m(5gR)R⇒N=5mg+mgcosθ>0 so block does not leave circular motion
fr=maT for limiting case μN=maT⇒μ(mg(5+cosθ))=mgsinθ⇒μ=sinθ5+cosθ
dμdθ=(5+cosθ)(cosθ)−sinθ(−sinθ)(5+cosθ)2=0⇒cosθ=−15
μmax=√1−1255−15=2√624⇒x=8
Similar Questions
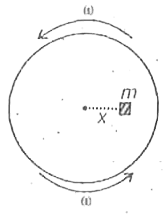
A cylinder with radius R spins about its horizontal axis with angular speed ω. There is a small block lying on the inner surface of the cylinder. The coefficient of friction between the block and the cylinder is μ. Find the value of ω for which the block does not slip, i.e., stays at rest with respect to the cylinder.
View SolutionA block of mass m is kept on horizontal turn table at x distance from the centre. If coefficient of friction between block and surface of turn table is μ, then maximum angular speed of the table so that block does not slip
View Solution
Knowledge Check
A block of mass 10 kg is placed on the rough horizontal surface. A pulling force F is acting on the block which makes an angle θ above the horizontal. If coefficient of friction between block and surface is 43 then minimum value of force required to just move the block is (g=10ms2)
A80 NB160 NC60 ND120 NA hollow cylinder of radius R rotates about its axis which is vertical. A block remains in contact with the inner wall if the frequency of rotation is f hertz, but falls at lower frequaencies. The coefficient of friction between the block and the cylinder is
Ag2π2f2RBg4π2f2RCgπ2RD2gπ2f2RA block is kept on a rough horizontal surface as shown. Its mass is 2 kg and coefficient of friction between block and surface (μ)=0.5. A horizontal force F is acting on the block. When
 AF = 4 N, acceleration is zero.BF = 4 N, friction is 10 N and acceleration is 3m/s2.CF = 14 N, acceleration is 2m/s2.DF = 14 N, friction is 14 N.
AF = 4 N, acceleration is zero.BF = 4 N, friction is 10 N and acceleration is 3m/s2.CF = 14 N, acceleration is 2m/s2.DF = 14 N, friction is 14 N.
A disc of radius 4m is rotating about its fixed centre with a constant angular velocity 2rads (in the horizontal plane).A block is also rotating with the disc without slipping. If co-efficient of friction between the block and the disc is 0.4 ,then the maximum distance at which the block can rotate without
View SolutionA block of mass m is pulled by a constant power P placed on a rough horizontal plane. The coeficient of friction between the block and surface is μ. Find the maximum velocity of the block.
View SolutionA block of mass m ios pulled by a constant power P placed on a rough horizontal plane. The friction co-efficient between the block and surface is μ. Find maximum velocity of the block.
View SolutionA block of mass m is kept over another block of mass 2m. Coefficient of friction between two blocks is μ and that of between lower blood from the horizontal surface is zero. A horizontal force F=43μmg is applied on the block of mass 2m. Acceleration of lower block is
View SolutionFind the minimum value of horizontal force (F) required on the block of mass m to keep it at rest on the wall. Given the coefficient of friction between the surfaces is μ.

View Solution

