Consider a conducting circular loop placed in a magentic filed as shown. When magnetic field changes with time, magentic flux also changes and emf is induced.
e=−dϕdt
If resistance of loop is R then induced current.
i=eR
For Current, charge must have come into motion. Magnetic force cannot make the statinoary charges to move. Actually there is an induced electric field in the conductor caused by changing magnetic flux, which make the change to move
∫→E.d→l=e=−dϕdt
This induced electric field is non-electrostatic by nature. line integral of →E around a closed path is non-zero

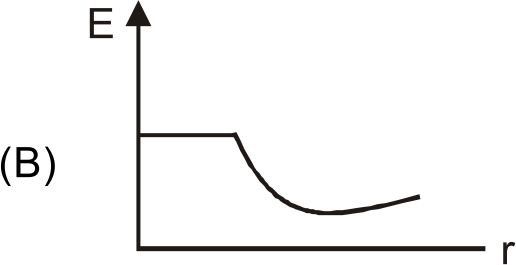
The magnetic field within cylindrical region whose cross - section is indicated starts increasing at a constant rate α tesla/sec The graph showing the variation.of induced electric field with distance r from the axis of cylinder is :
A

B
C
D

Video Solution
Text Solution
Explanation:
For rlt R ∮Edl=AdBdt
E2πr=(πr2)α
E=rα2 or E∝r
So, E-r graph is a straight line passing through origin.
At r=R, E=Rlapha2
for rgtR E2πr=(πR2)α
Hence , choice (a) is correct and choices (b),(c) and (d) are wrong.
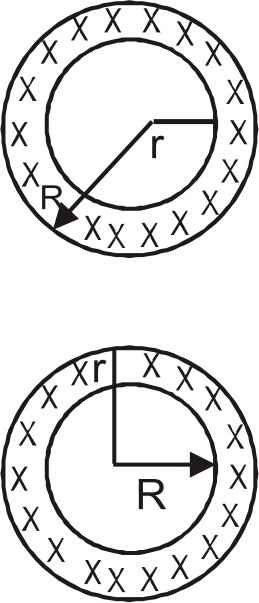
|
Similar Questions
Knowledge Check
Consider a conducting circular loop placed in a magentic filed as shown. When magnetic field changes with time, magentic flux also changes and emf is induced.
e=−dϕdt
If resistance of loop is R then induced current.
i=eR
For Current, charge must have come into motion. Magnetic force cannot make the statinoary charges to move. Actually there is an induced electric field in the conductor caused by changing magnetic flux, which make the change to move
∫→E.d→l=e=−dϕdt
This induced electric field is non-electrostatic by nature. line integral of →E around a closed path is non-zero

Refer to above questions, Find the magnitude of line integral of induced electric field along path CD.A40 mVB60 mVC80 mVDzeroConsider a conducting circular loop placed in a magentic filed as shown. When magnetic field changes with time, magentic flux also changes and emf is induced.
e=−dϕdt
If resistance of loop is R then induced current.
i=eR
For Current, charge must have come into motion. Magnetic force cannot make the statinoary charges to move. Actually there is an induced electric field in the conductor caused by changing magnetic flux, which make the change to move
∫→E.d→l=e=−dϕdt
This induced electric field is non-electrostatic by nature. line integral of →E around a closed path is non-zero

A square non- conducting loop 20 cm on a side is placed in a magnetic field The centre of side AB coincides with the centre of magnetic field The magnetic field is increasing at the rate of 2T/s. Find the magnitude of line integral of induced electric field along path BC.
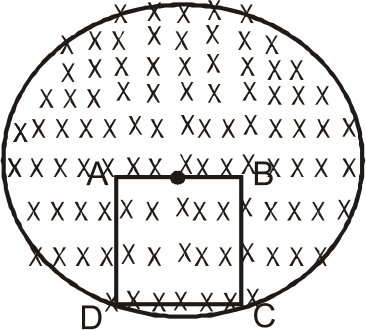 A10 mVB20 mVC30 mVDzero
A10 mVB20 mVC30 mVDzeroElectric field induced by changing magnetic fields are
AConservativeBNon-conservativeCMay be conservatie or non-conservative depending on the conditionDNothing can be said
Induced electric field due to changing magnetic field
View SolutionA: When a conducting loop is kept stationary in a non-uniform magnetic field an emf is induced.
R: As per Faraday's law, whenever flux changes, an emf is induced.
View SolutionA circular loop is placed in magnetic field B=2t. Find the direction of induced current produced in the loop.

View SolutionA triangular loop is placed in a dot ⊙ magnetic field as shown in figure. Find the direction of induced current in the loop if magnetic field is increasing.
View SolutionDirection of induced current produced by motion of a conductor in a magnetic field is given by
View Solution

