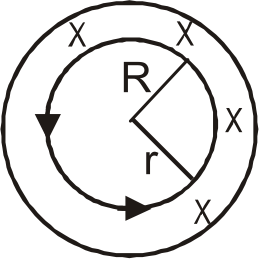
Time varying magnetic filed is present in a circular region of radius R. Match the proper entries from column-2 to column-1 using the codes given below the columns,
Column IColumn II(P) An unsteady magnetic field(1) Electric field is perpendicular to the length of rod (Q)Induced electric field at a point within magnetic field (r gtR)(2)r2dBdt(R)Induced electric field at a point out side the magnetic field (r lt R)(3)R22rdBdt(S)If a rod is placed along the diameter of the magnetic field(4) induced electric field
A
PQRS(A)3214
B
PQRS(B)2134
C
PQRS(C)4213
D
PQRS(D)4231
Video Solution
Text Solution
Explanation :
time varying magnetic field produced electric field unknown as induced electric field.
So (P)→(4)
for flt R
∮E.DI=−AdBdt
E2πr=−πr2dBdt
E=−r2dBdt
So, (Q)→(2)
For rgt R
E2pr=−πR2dBdtss,E=−R22rdBdt
So (R)→(3)
If rod ris placed along the diameter of magnetic field, then electric field is perpendicular to length of rod.
|
Similar Questions
Knowledge Check
Electric field induced by changing magnetic fields are
AConservativeBNon-conservativeCMay be conservatie or non-conservative depending on the conditionDNothing can be saidElectric field at a point varies as r0 for
AAn electric dipoleBA point chargeCA plane infinite sheet of chargeDA line charge of infinite lengthA time varying magnetic field B=Kr3t is existing in a cylindrical region of radius 'R' as shown (where k is a constant). The induced electric field 'E' at rR2 is
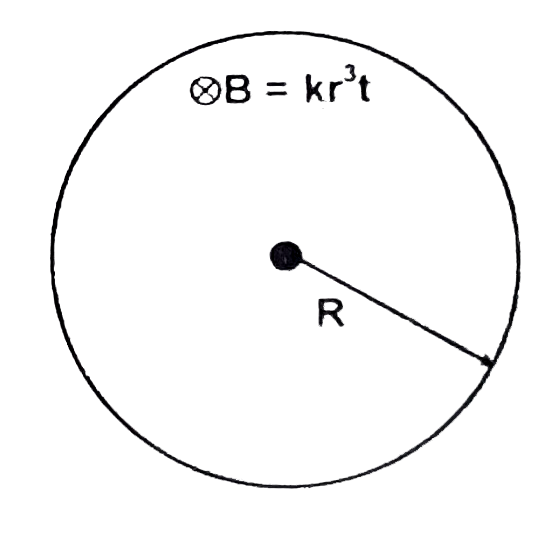 AKR420BKR440CKR460DKR480
AKR420BKR440CKR460DKR480
Induced electric field due to to changing magnetic flux are more readily observed than induced magnetic field due to changing electric field. Why?
View SolutionThe magnetic field perpendicular to the plane of a conducting ring of radius r change ate the rate dBdt
View SolutionAssertion : Magnetic force is always perpendicualr to the magnetic field.
Reason : Electric force is along the direction of electric field.
View SolutionA conducting ring of radius r is placed in a varying magnetic field perpendicular to the plane of the ring. If the rate at which the magnetic field varies is x, the electric field intensity at any point of the ring is
View SolutionElectric field intensity at a point varies as r−3 for
View Solution


