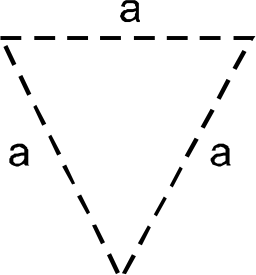
All sides of an equilateral triangle are diameter of three identical uniform semi- circular rings each of mass m. Plane of each ring is perpendicular to the plane of paper. Then moment of inertia of this system of three semicircular rings about an axis through centroid of triangle and perpendicular to plane of paper is :
5ma224
5ma216
5ma28
5ma26
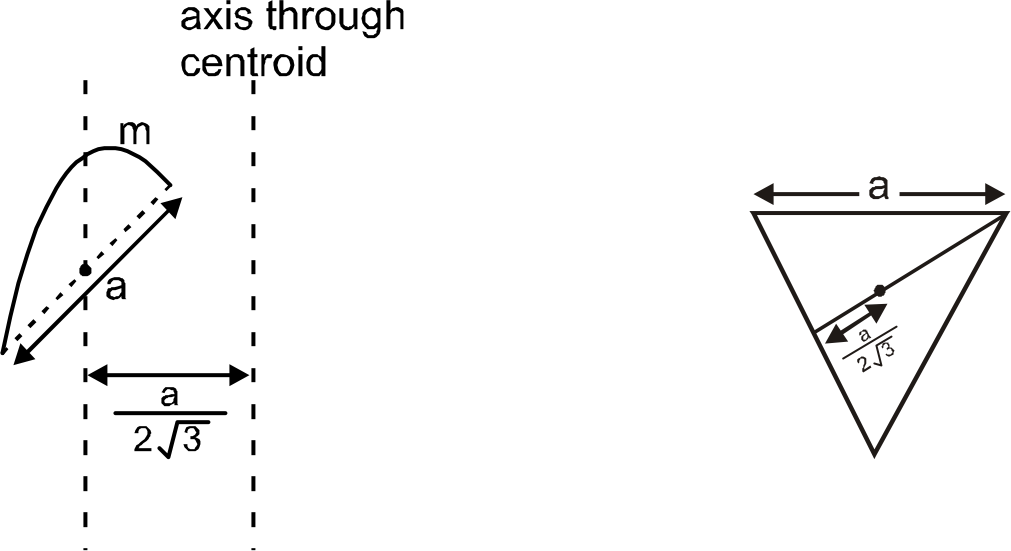
I'=Icm+m(a2√3)2=5ma224=Icm=m(a2)22=ma28
I=3I'=5ma28
Similar Questions
Derive an expression for moment of inertia of a thin circular ring about an axis passing through its centre and perpendicular to the plane of the ring.
View SolutionThe moment of inertia of a uniform circular ring, having a mass M and a radius R, about an axis tangential to the ring and perpendicular to its plane, is
View Solution
Knowledge Check
Moment of inertia of a circular ring about an axis through its centre and perpendicular to its plane is
AI=12MR2BI=MR2CI=32MR2DI=52MR2Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A1/2MR2BMR2C1/4MR2D3/4MR2The moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is
A12Mr2BMt2C25Mr2D14Mr2
Calculate the moment of inertia of a ring of mass 2 kg and radius 50 cm about an axis passing through its centre and perpendicular to its plane
View SolutionFrom a ring of mass M and radius R, a 30o sector is removed. The moment of inertia of the remaining portion of the ring, about an axis passing through the centre and perpendicular to the plane of the ring is
View SolutionFrom a complete ring of mass M and radius R, a 30∘sector is removed. The moment of inertia of the incomplete ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is
 ,
,
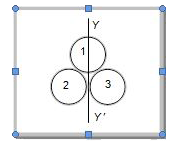
View SolutionThree rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY¢ will be
View SolutionTwo identical concentric rings each of mass m and radius R are placed perpendicularly. What is the moment of inertia of the system about the axis of one of the rings ?
View Solution

