A uniform rod of mass 200 grams and length L = 1m is initially at rest in vertical position. The rod is hinged at centre such that it can rotate freely without friction about a fixed horizontal axis passing through its centre. Two particles of mass m = 100 grams each having horizontal velocity of equal magnitude u = 6 m/s strike the rod at top and bottom simultaneously as shown and stick to the rod. Find the angular speed (in rad/sec.) of rod when it becomes horizontal.
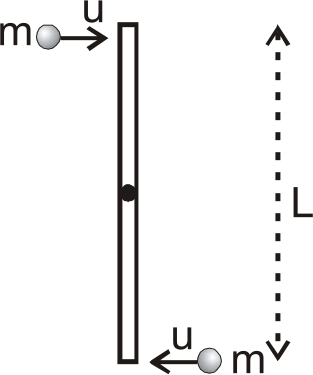
From conservation of angular momentum
muL2+muL2=[2mL212+m(L2)2+(L2)2]ω
muL=[mL26+mL24+mL24]ω=2mL23ω or ω=3u2L=3×62×1=9rad/sec
Similar Questions
A uniform rod of mass M and length L is hinged at its end. The rod is released from its vertical position by slightly pushing it. What is the reaction at the hinge when the rod becomes horizontal, again vertical.
View SolutionA uniform rod of mass m and length l can rotate in a vertical plane abota smooth horizontal axis hinged at point H. Find the force exerted by the hinge just after rod is released from rest, from initial horizontal position?

View Solution
Knowledge Check
A uniform rod of mass 20 Kg and length 1.6 m is piovted at its end and swings freely in the vertical plane. Angular acceleration of the rod just after the rod is relased from rest in the horizontal position is
 A15g16B17g16C16g15Dg15
A15g16B17g16C16g15Dg15A uniform rod AB hinged about a fixed point P is initially vertical. A rod is released from vertical position. When rod is in horizontal position:

The acceleration of the centre of mass of the rod isA−6g7ˆi−12g7ˆjB−12g7ˆi−6g7ˆjC−3g7ˆi−9g7ˆjD−9g7ˆi−3g7ˆjConsider a rod of mass M and length L pivoted at its centre is free to rotate in a vertical position plane. The rod is at rest in the vertical position. A bullet of mass M moving horizontally at a speed v strikes and embedded in one end of the rod. The angular velocity of the rod just after the collision will be.
Av/LB2v/LC3v/2LD6v/L
A rod of mass 12 m and length l lying on a smooth horizontal plane can rotate freely about a stationary, vertical axis passing through the rod's end. A particle of mass m moving along the plane with speed v0 hits the rod's end perpendicularly and gets stuck there. Find the angular velocity of the system.

View SolutionA uniform rod of mass M and length L with two particles m and m2 attached to its ends, is pivoted at its centre. The system rotates in a vertical plane with angular velocity ω.

View SolutionA thin uniform rod of length l and mass m is swinging freely about a horizontal axis passing through its end. Its maximum angular speed is ω. Its centre of mass rises to a maximum height of -
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionThe radius of gyration of an uniform rod of length L about an axis passing through its centre of mass and perpendicular to its length is.
View Solution
