In a certain gravity free space, the piston of an injection is being pushed so that the water jet comes out with a speed v. The area of the piston is much greater than the orifice of the injection.
The force required to be applied on the piston is proportional to v2.
The power developed by the force pushing the piston is proportional to v3.
The time for emptying the injection is proportional to v−1.
The total work done in emptying the injection is proportional to v2.
FA+12ρv'2=12ρv2 (i)
A'v'=Av(ii)
∴F∝v2(A)
P=F.v'(B)
Av=volume flow rate =volume/t
∴t∝1v(C)
W.D.=ΔK⇒(D)

Similar Questions
A long cylindrical tank of cross-section area 0.5m2 is filled with water. It has an opening at a height 50 cm from the bottom, having area of cross-section 1×10−4m2. A movable piston of cross-section area almost equal to 0.5m2 is fitted on the top of the tank such that it can slide in the tank freely. A load of 20 kg is applied on the top of the water by piston, as shown in the figure. Find the speed of the water jet with which it hits the surface when piston is 1m above the bottom. (Ignore the mass of the piston). If this speed is (18x) m/s, find the value of x.
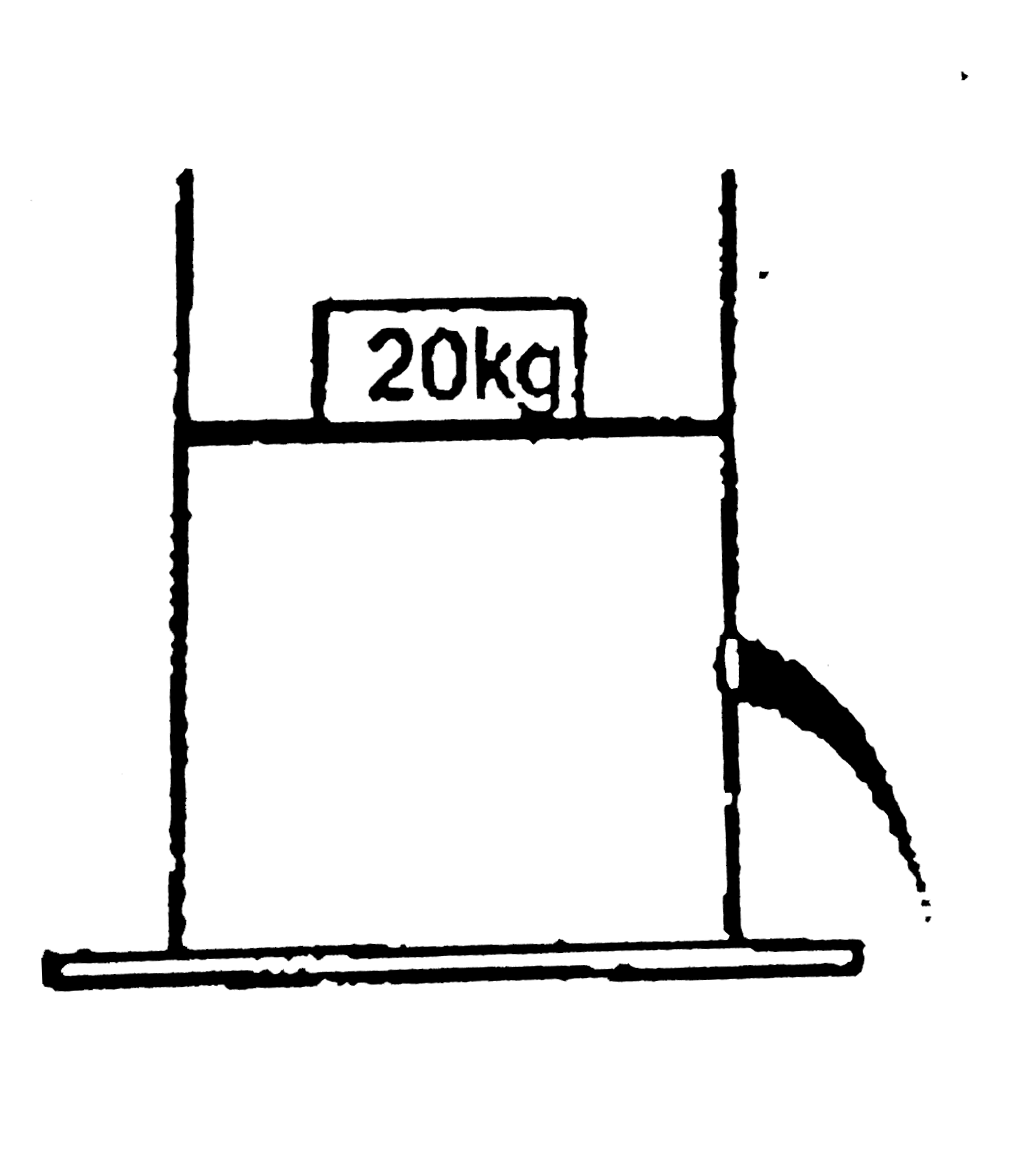
View SolutionA long cylindrical tank of cross-sectional area 0.5m2 is filled with water. It has a small hole at a height 50cm from the bottom. A movable piston of cross-sectional area almost equal to 0.5m2 is fitted on the top of the tank such that it can slide in the tank freely. A load of 20kg is applied on the top of the water by piston, as shown in the figure. Calculate the speed of the water jet with which it hits the surface when piston is 1m above the bottom. (Ignore the mass of the piston)

View Solution
Knowledge Check
An initially empty beaker, in the shape of a cylinder with cross sectional area A, is left out in th rain. The raindrops hit the beaker vertically downward with speed v. The rain continues at a constant rate, so the height of the water in the beaker h(t) increases with time t at a rate dh/dt=u, where u is small compared to v. The raindrops quickly come to rest inside the beaker, so we can neglect any kinetic energy of the water that has collected in the beaker. Let p denote the density of water (i.e., the mass per unit volume)
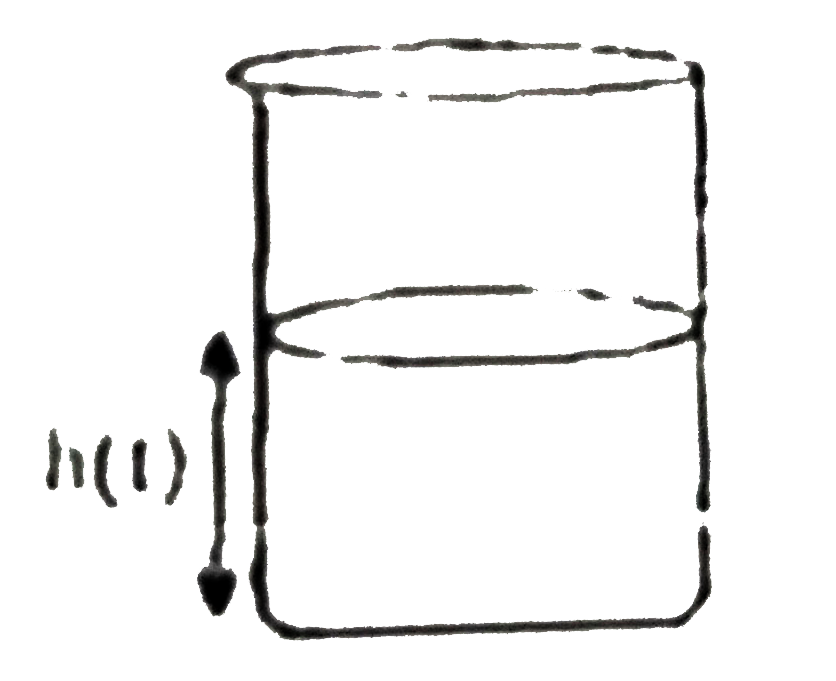
Choose the incorrect option.ARate at which the mass of the water in the beaker increaes with time is Pau.BAt a given time the water in the beaker has total vertical momentum.CThe mass of the water in the beaker at a given time is pADnone of the above optionsAn initially empty beaker, in the shape of a cylinder with cross sectional area A, is left out in th rain. The raindrops hit the beaker vertically downward with speed v. The rain continues at a constant rate, so the height of the water in the beaker h(t) increases with time t at a rate dh/dt=u, where u is small compared to v. The raindrops quickly come to rest inside the beaker, so we can neglect any kinetic energy of the water that has collected in the beaker. Let p denote the density of water (i.e., the mass per unit volume)

Ley ycm(t) denote the height of the centre of mass of all the water that has collected in the beaker by time t. what is the rate at which this height increaes (i.e. dy(cm)/dt?AuBu2CVolume strengthDv2An initially empty beaker, in the shape of a cylinder with cross sectional area A, is left out in th rain. The raindrops hit the beaker vertically downward with speed v. The rain continues at a constant rate, so the height of the water in the beaker h(t) increases with time t at a rate dh/dt=u, where u is small compared to v. The raindrops quickly come to rest inside the beaker, so we can neglect any kinetic energy of the water that has collected in the beaker. Let p denote the density of water (i.e., the mass per unit volume)
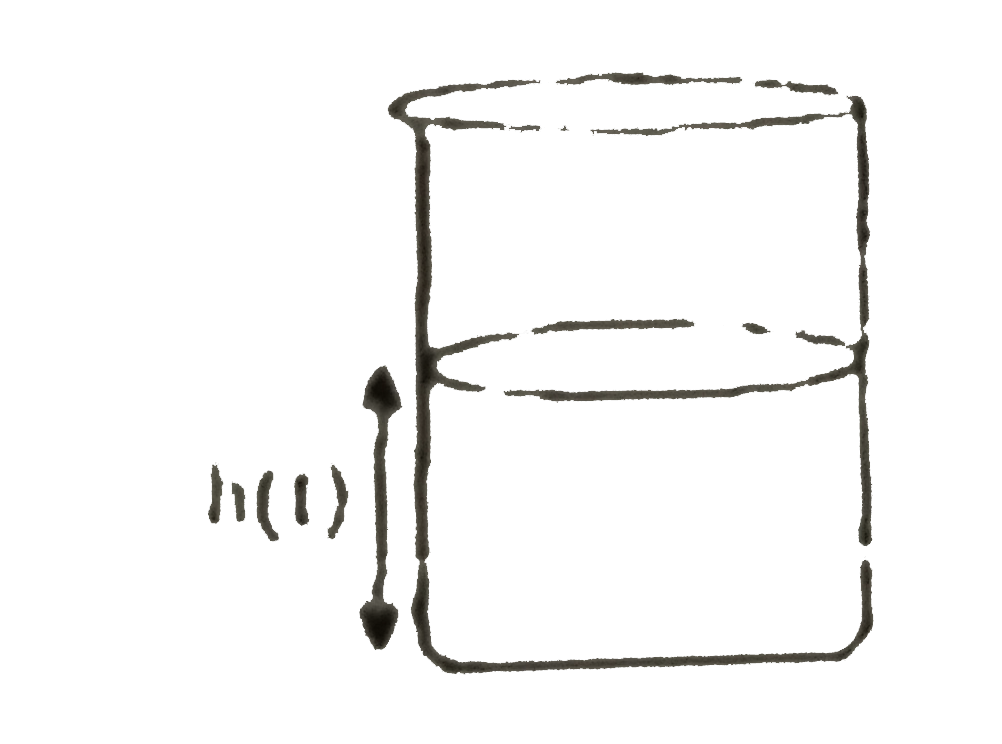
If the beaker is placed on a weighing scale, while the beaker is wstill in the rain, the impact of the raindrops on the beaker will cause the reading on the scale increased by the impact of the raindrops ? (Neglect the effect of raindrops that hit the scale directily).ApAv2gBpAu2gCpAuVgDpAuv2g
Figure shows a liquid being pushed out of a tube by pressing a piston. The area of cross section of the piston is 1.0 cm^2 and that of the tube at the outlet is 20mm2. If the piston is pushed at a speed of 2cms−1. What is the speed of the outgoing liquid?

View SolutionWhat work should be done in order to squeeze all water from a horizontally located cylinder (figure) during the time t by means of a constant force acting on the piston? The volume of water in the cylinder is equal to V, the cross-sectional area of the orifice to s, with s being considerably less than the piston area. The friction and viscosity are negligibly small.

View Solution
An ideal liquid of density ρ is filled in a horizontally fixed syringe fitted with a piston. There is no friction between the piston and the inner surface of the syringe. Cross-sectional area of the syringe is A. At one end of the syringe, an orifice is made. When the piston is pushed into the syringe, the liquid comes out of the orifice and then following a parabolic path falls on the ground.
With what velocity does the liquid come out of the orifice?
View SolutionA spray gun is shown in the figure where a piston pushes air out of a nozzle. A thin tube of uniform cross section is connected to the nozzle. The other end of the tube is in a small liquid container. As the piston pushes air through the nozzle, the liquid from the container rises into the nozzle and is sprayed out. For the spray gun shown, the radii of the piston and the nozzle are 20mm and 1mm respectively. The upper end of the container is open to the atmosphere.

If the piston is pushed at a speed of 5mms−1, the air comes out of the nozzle with a speed of
View Solution
An ideal liquid of density ρ is filled in a horizontally fixed syringe fitted with a piston. There is no friction between the piston and the inner surface of the syringe. Cross-sectional area of the syringe is A. At one end of the syringe, an orifice is made. When the piston is pushed into the syringe, the liquid comes out of the orifice and then following a parabolic path falls on the ground.
With what velocity the liquid strikes the ground?
View Solution

