Find the constant of intergration by the general solution of the differential equation (2x2y−2y4)dx+(2x3+3xy3)dy=0 if curve passes through (1,1).
The correct Answer is:1
Step by step video, text & image solution for Find the constant of intergration by the general solution of the differential equation (2x^(2)y-2y^(4))dx+(2x^(3)+3xy^(3))dy=0 if curve passes through (1,1). by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIAL EQUATION Book:ARIHANT MATHSChapter:DIFFERENTIAL EQUATION Exercise:Exercise (Subjective Type Questions)
Explore 4 Videos
- DIFFERENTIAL EQUATION Book:ARIHANT MATHSChapter:DIFFERENTIAL EQUATION Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 26 Videos
- DIFFERENTIAL EQUATION Book:ARIHANT MATHSChapter:DIFFERENTIAL EQUATION Exercise:Differential Equations Exerise 5 :
Explore 2 Videos
- DETERMINANTS Book:ARIHANT MATHSChapter:DETERMINANTS Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 18 Videos
- DIFFERENTIATION Book:ARIHANT MATHSChapter:DIFFERENTIATION Exercise:Exercise For Session 10
Explore 4 Videos
Similar Questions
A hemi-spherical tank of radius 2 m is initially full of water and has an outlet of 12cm2 cross-sectional area at the bottom. The outlet is opened at some instant. The flow through the outlet is according to the law v(t)=√0.62gh(t), where v(t) and h(t) are, respectively, the velocity of the flow through the outlet and the height of water level above the outlet and the height of water level above the outlet at time t, and g is the acceleration due to gravity. Find the time it takes to empty the tank.
View SolutionIf f:R−{−1}→Randf is differentiable function satisfies:
f((x)+f(y)+xf(y))=y+f(x)+yf(x)∀x,
y∈R−{_1} Find f(x).
View SolutionMatch the following :
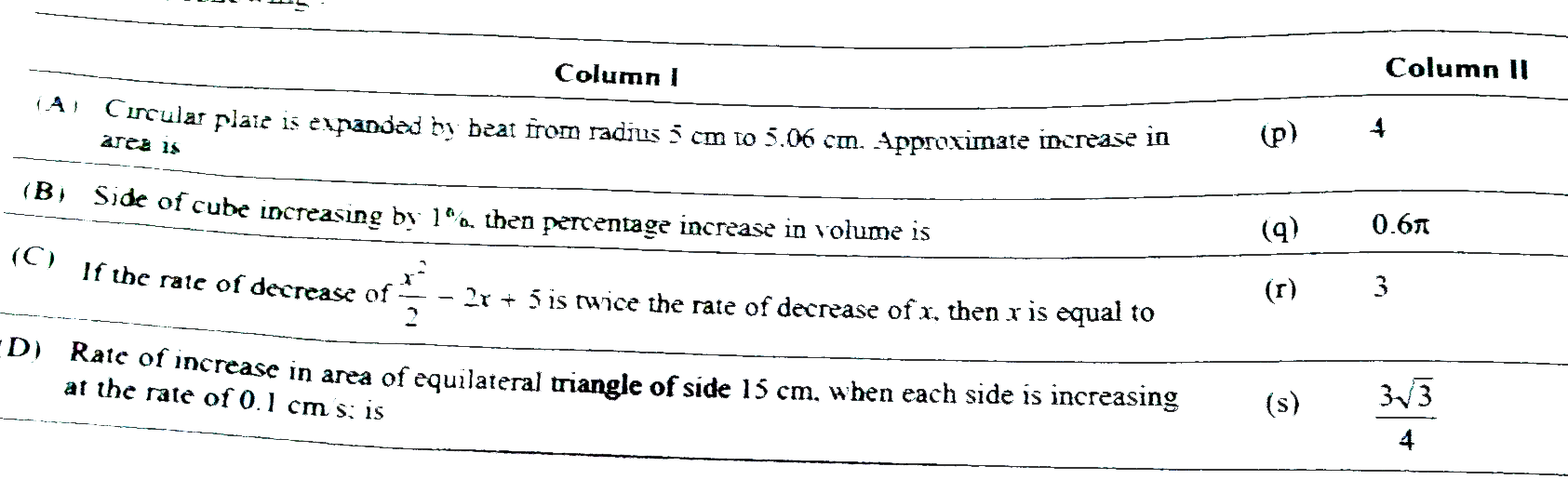
View SolutionIf a2+b2+c2=-2 and f(x)= ∣∣ ∣ ∣∣1+a2x(1+b2)x(1+c2)x(1+a2)x1+b2x(1+c2)x(1+a2)x(1+b2)x1+c2x∣∣ ∣ ∣∣ then f(x) is a polynomial of degree
View SolutionThe function f(x)=ex+x, being differentiable and one-to-one, has a differentiable inverse f−1(x). The value of ddx(f−1) at the point f(log2) is 11n2 (b) 13 (c) 14 (d) none of these
View SolutionThe solution of the differential equation
(2y−1)dx−(2x+3)dy=0, is
View SolutionWhat is the general solution of the differential equation x2dy=y2dx=0 ?
where c is the constant of intergration.
View Solutionबिंदु (1,1) से गुजरने वाले एक ऐसे वक्र का समीकरण ज्ञात कीजिए जिसका अवकल समीकरण xdy=(2x2+1)dx(x≠0) है।
View Solutionअवकल समीकरण xydydx=(x+2)(y+3) के लिए बिन्दु (1,1) से गुजरने वाला वक्र ज्ञात कीजिए ।
View Solutionबिंदु (1,1) से गुजरने वाले एक ऐसे वक्र का समीकरण कीजिए जिसका अवकल समीकरण x∗dy=(2x2+1)∗dx(x≠0) है ।
View SolutionThe solution of the differential equation (2y−1)dx−(2x+3)dy=0 is -
View SolutionThe equation of the curve passing through the point (1,1) and satisfying the differential equation dydx=x+2y−3y−2x+1 is
View Solutionअवकल समीकरण (2y−1)dx−(2x+3)dy=0 का हल है
View Solutionअकलन समीकरण (x−y−2)dx−(2x−2y−3)dy=0 का हल ज्ञात कीजिये।
View SolutionThe general solution of the differential equation 2xdydx−y=3 is a family of
View SolutionFind the equation of the curve passing through the point (1,1) whose differential equation is x dy = (2x2+1)dx(x≠0).
View Solution
