एक ताल निर्देशाक्षों से A, B, C पर इस प्रकार मिलता है कि ΔABC का केन्द्रक बिंदु (a,b,c) है | सिद्ध कीजिये कि तल का समीकरण xa+yb+zc=3 है |
माना कि तल की समीकरण है, xα+yβ+zγ=1 ...(1)
यदि तल x,y तथा z - अक्षो से क्रमशः A, B, C पर मिलता है तो A, B, C के निर्देशांक क्रमशः (α,0,0),(0,β,0) एवं (0,0,γ) होंगे |
इस प्रकार ΔABC के केन्द्रक (centroid ) के निर्देशांक (α3,β3,γ3) होंगे |
लेकिन दिया हुआ है कि ΔABC का केन्द्रक (a,b,c) है |
∴α3=a,β3=b,γ3=c
∴α=3a,β=3b,γ=3c.
अतः तल का अभीष्ट समीकरण है :
xa+yb+zc=3
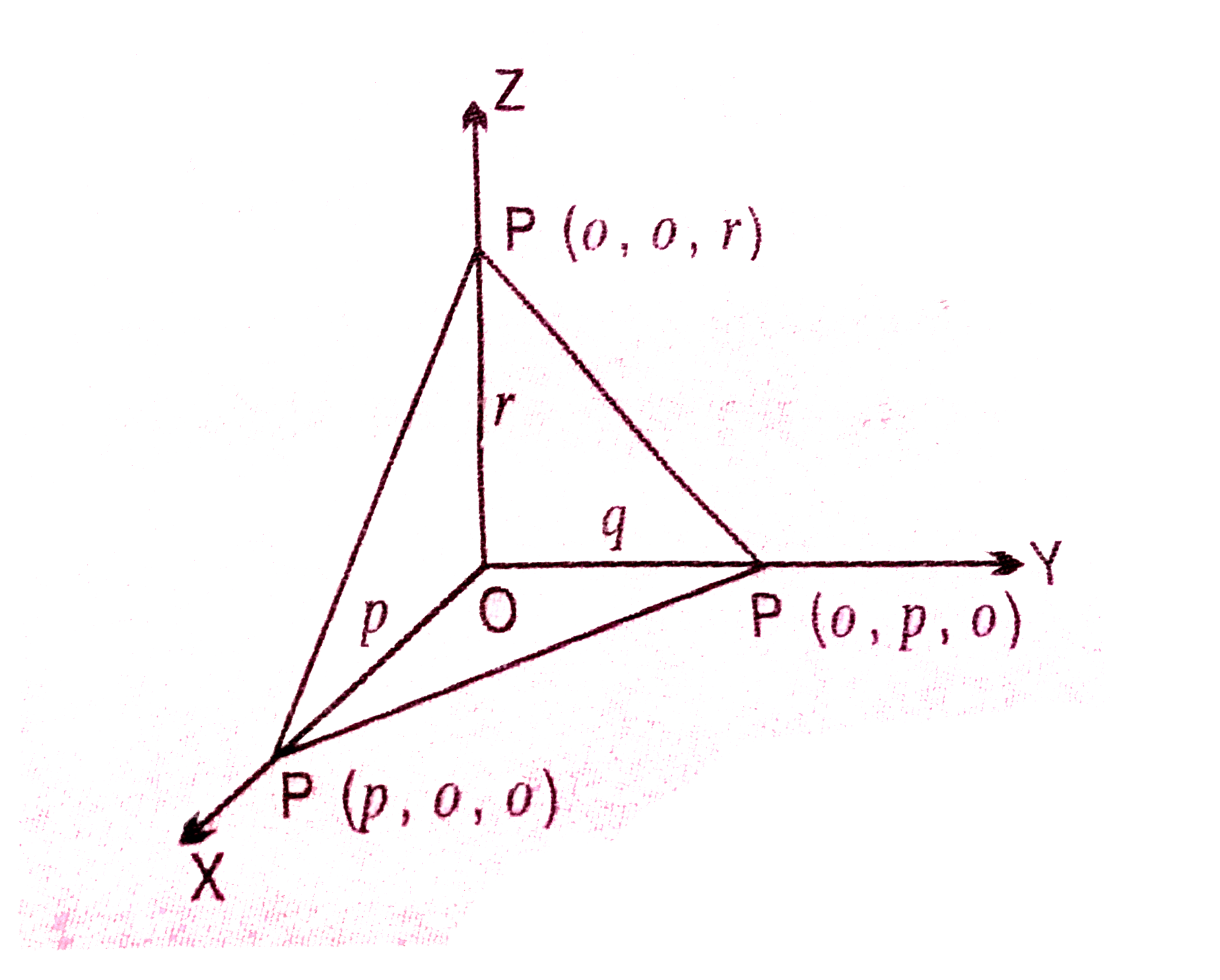
Topper's Solved these Questions
Similar Questions
एक शंकु की ऊँचाई में वृद्धि 2% है तथा इसका अर्ध शीर्ष कोण अपरिवर्तित है। इसके (i) कुल पृष्ठ क्षेत्रफल (ii) आयतन में
सन्निकट प्रतिशत बढ़ोतरी वृद्धि क्या है?
View Solutionकिसी त्रिभुज ABC में A (a, 0) और B (-a, 0) बिंदु है । शीर्ष C इस प्रकार गमन करता है कि tanA+tanB=2 . बिंदु C का बिन्दुपथ ज्ञात कीजिए ।
View Solutionउस बिंदु का बिन्दुपथ जो इस प्रकार गमन करता है कि बिंदु की दोनों अक्षों से दूरी सदैव समान रहती है ………… होगा ।
View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionयदि संक्रिया ∗ वास्तविक संख्याओं के समुच्चय R पर द्विआधारी संक्रिया है तथा इस प्रकार परिभाषित है कि
a∗b=√a4+b4 , जहाँ a,b∈R से दिखाइए कि '∗' क्रम-विनिमेय नियम का पालन करती है।
View Solutionएक नली में 12 सेमी.3/से. कि दर से बालू उंडेली जा रही है। उंडेली गई बालू से एक शंकु का निर्माण इस प्रकार होता है कि शंकु कि ऊंचाई सदैव आधार कि त्रिज्या का 16 वा भाग होती ह। बालू के शंकु कि ऊंचाई में किस गति से वृद्धि हो रही है जबकि ऊंचाई 4 सेमी. है ?
View Solutionएक समतल निर्देशांकों अक्षों को A,B,C पर इस प्रकार मिलता है कि त्रिभुज ABC का केंद्रक (1,2,3) है तो समतल का समीकरण होगा
View Solutionएक समतल निर्देशांक अक्षो को A,B,C पर इस प्रकार मिलता है की त्रिभुज ABC का केन्द्रक (1,2,3) है तो समतल का समीकरण होगा-
View Solution

